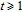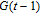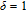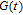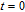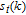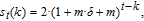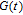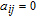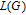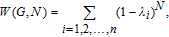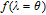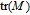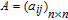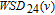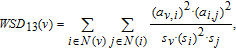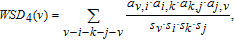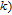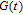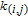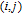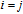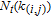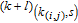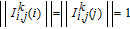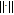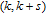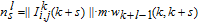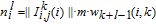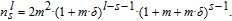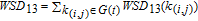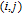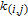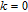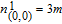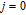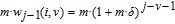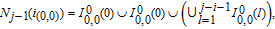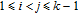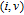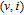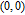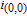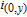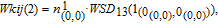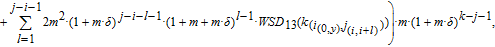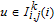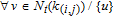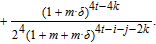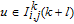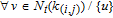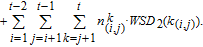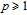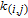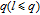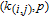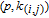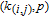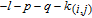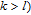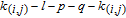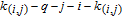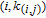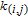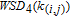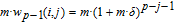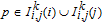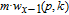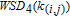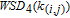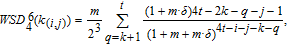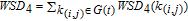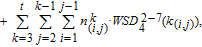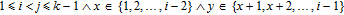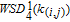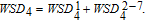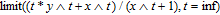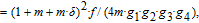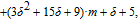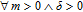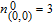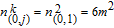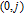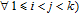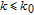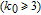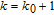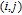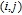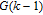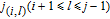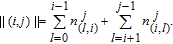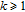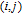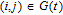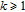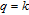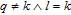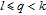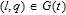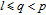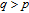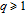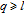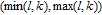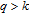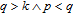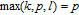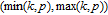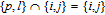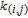1. IntroductionThe weighted spectral distribution (WSD) is a metric defined on the normalized Laplacian spectrum. Although the WSD is first proposed[1–3] for the study of Internet topologies, our recent work[4–7] has demonstrated that the WSD is a good indicator for distinguishing diverse evolving physical systems. Additionally, we explained the physical meaning of the WSD in Internet topologies,[8] that is, the metric indicates the transformation from single-homed to multi-homed networks. Also, we designed an algorithm[9] for calculating the WSD which induces that the metric can be applied to networks with more than millions of nodes. However, these studies[1–9] focused on unweighted networks. To rigorously analyze the WSD in diachronic networks which focus on the time evolution and are similar to dynamical processes in nature,[10] we have designed a tree model[5] and a scale-free model.[6] However, the two models’ clustering coefficients are strictly zero. Furthermore, the γ exponent of the degree distribution
 of the used scale-free models[6, 7] is one, whereas the γ exponent of most real evolving scale-free networks falls in a range between two and three.[11] Therefore, in this paper, we rigorously study the WSD on diachronic weighted small-world scale-free networks which have more reasonable γ exponents.
of the used scale-free models[6, 7] is one, whereas the γ exponent of most real evolving scale-free networks falls in a range between two and three.[11] Therefore, in this paper, we rigorously study the WSD on diachronic weighted small-world scale-free networks which have more reasonable γ exponents.
Synchronic random models are rigorous tools to analyze many graph metrics,[12] e.g., average path length and graph spectra. However, these models consider the statistical ensemble of graphs at a fixed time point and cannot capture the dynamical process in nature.[10] For diachronic networks, both random models[13–16] and deterministic models[17–23] have received much attention. Specifically, deterministic models are suitable for the rigorous analysis of more graph metrics, e.g., diameter, clustering coefficients, graph matrices, and graph spectra. The first deterministic scale-free model was proposed by Barabasi et al.[20] Another elegant model, called pseudo fractral scale-free web (PSW), was introduced by Dorogovtsev et al.[11] The PSW has been extended to many versions,[21–23] and the latest version proposed by Zhang et al.[23] is called deterministic weighted scale-free small-world network (WSSN) model. The WSSN model has highly tunable exponents for three power-law distributions of node degree, node strength, and edge weight. Additionally, all of the exponents fall in a range between 2 and 3 and the average clustering coefficient of the model is high and independent of the network order. These features of this model might lead to a better understanding of realistic networks. Therefore, in this paper, we rigorously study the WSD by using the WSSN model.
Currently, the scaling feature of many graph metrics has received much attention. The average receiving time is defined as the average of the mean first-passage times for a random walker to a given hub node in a graph, averaged over all source points in the graph.[24] Dai and Sun et al.[25–27] studied the average receiving time and the average weighted receiving time in deterministic Koch and hierarchical network models and found that the average receiving time grows sublinearly with increasing network order and the average weighted receiving time grows as power-law function of the network order. The Kemeny constant is defined as the expected time for a walker starting from a node to another node selected randomly from all nodes.[28] Zhang et al.[29] studied the Kemeny constant in deterministic scale-free fractal networks and found that the Kemeny constant scales linearly with network order. Additionally, many graph metrics (e.g., degree distribution, clustering coefficient, and spectral radius)[30–32] can be used to capture the unaltered features of evolving systems. As one number of these graph metrics with scaling features, this study on the WSD is helpful for a better understanding of evolving weighted and small-world systems.
2. WSSN modelThe WSSN model is controlled by two parameters m and δ. Zhang et al.[23] denoted the network after t steps of the model by
 . Specifically, the network is constructed as follows.[23] For
. Specifically, the network is constructed as follows.[23] For
 ,
,
 is a triangle consisting of three links with unit weight. For
is a triangle consisting of three links with unit weight. For
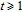 ,
,
 is obtained from
is obtained from
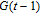 :
:
 new nodes are added for each of the links with weight w in
new nodes are added for each of the links with weight w in
 , and each new node is connected to both ends of this link in
, and each new node is connected to both ends of this link in
 by two new links of unit weight; moreover, the weight of these links in
by two new links of unit weight; moreover, the weight of these links in
 is increased by
is increased by
 . It is noteworthy that m and δ are positive integers. When
. It is noteworthy that m and δ are positive integers. When
 and
and
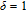 , the constructed networks
, the constructed networks
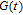 with
with
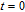 , 1, and 2 are shown in Fig. 1.
, 1, and 2 are shown in Fig. 1.
In
 , we represent all nodes added at step k as k and let
, we represent all nodes added at step k as k and let
 denote an edge linking two nodes i and j for
denote an edge linking two nodes i and j for
 . If
. If
 , both i and j must be zero. Then, according to the study of Zhang et al.,[23] the strength
, both i and j must be zero. Then, according to the study of Zhang et al.,[23] the strength
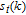 of node k and the weight
of node k and the weight
 of edge
of edge
 in
in
 can be expressed as
can be expressed as
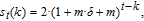 | (1) |
 | (2) |
where the strength of a node is defined as the sum over all weights of edges that are connected to the node.
Additionally, Zhang et al.[23] derived the number of all nodes in
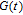 as
as
 | (3) |
3.
 in weighted networks
in weighted networksTo this day, the study on the WSD has been restricted to unweighted networks. Let
 denote a simple and undirected graph where V and E are respectively node set and edge set, and d
v
denote the degree of node v in graph G. Let n denote the cardinality of node set V. If
denote a simple and undirected graph where V and E are respectively node set and edge set, and d
v
denote the degree of node v in graph G. Let n denote the cardinality of node set V. If
 is the adjacency matrix of graph G (
is the adjacency matrix of graph G (
 if there is an edge between nodes v
i
and v
j
and
if there is an edge between nodes v
i
and v
j
and
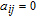 otherwise) and B is a diagonal matrix with
otherwise) and B is a diagonal matrix with
 , the normalized Laplacian matrix of graph G is defined as
, the normalized Laplacian matrix of graph G is defined as
 where I denotes the identity matrix.[1] Let λ
1,
where I denotes the identity matrix.[1] Let λ
1,
 denote all eigenvalues of matrix
denote all eigenvalues of matrix
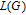 , called the normalized Laplacian spectrum of graph G. Then, the WSD is defined as[1]
, called the normalized Laplacian spectrum of graph G. Then, the WSD is defined as[1]
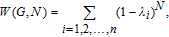 | (4) |
where 4 is the best selection of parameter
N.
[1–9]
Because all eigenvalues of
 fall in a range
fall in a range
 , Fay et al.
[1] transformed Eq. (4) into another expression as follows:
, Fay et al.
[1] transformed Eq. (4) into another expression as follows:
 | (5) |
where

denotes equally spaced intervals in

, and
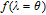
represents the number of eigenvalues falling in

. Note that
θ is an arbitrary value in

. When

, equation (
5) turns into Eq. (
4). According to Eq. (
5), the
WSD can be expressed by using the weighted sum of the normalized Laplacian spectral distribution, so it is called the “weighted spectral distribution”.
[1]
Additionally, Fay et al.[1] derived the following equation:
 | (6) |
where
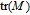
denotes the trace of matrix
M, and

denotes all
N-cycles in graph
G.
If G is an unweighted graph,
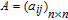 is a 0 − 1 matrix and node degree
is a 0 − 1 matrix and node degree
 . For this case, Fay et al.[1] obtained the following equation:
. For this case, Fay et al.[1] obtained the following equation:
 | (7) |
In this paper, we consider the WSD on weighted networks. Thus, entry a
ij
in A should be the weight of edge between nodes v
i
and v
j
, and entry
 in B should be the strength of node v
i
. Additionally, equation (6) holds for weighted networks. Therefore, for weighted networks, we can obtain
in B should be the strength of node v
i
. Additionally, equation (6) holds for weighted networks. Therefore, for weighted networks, we can obtain
 | (8) |
where
s
v
denotes the strength of node
v in graph
G.
4. Calculation method of WSD in weighted networksBased on Eq. (8), for the WSD calculation, it is critical to enumerate all N-cycles (4 is the best selection of
 in weighted graph G. Specifically, all 4-cycles can be classified as four patterns as shown in Fig. 2.[6, 7, 9]
in weighted graph G. Specifically, all 4-cycles can be classified as four patterns as shown in Fig. 2.[6, 7, 9]
It is noteworthy that the multiple edges between two nodes in these patterns are related to only one edge in weighted graph G that does not have any multiple edge. Let
 denote the set of neighbors of node v,
denote the set of neighbors of node v,
 represent the set of neighbors of node
represent the set of neighbors of node
 , and
, and
 refer to the set of common neighbors of nodes i and j with
refer to the set of common neighbors of nodes i and j with
 and
and
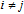 .
.
As an extension for unweighted graphs,[6] in weighted graph G, the sum over all 4-cycles associated with patterns 1 and 3
 , and the sum over all 4-cycles associated with patterns 2 and 4
, and the sum over all 4-cycles associated with patterns 2 and 4
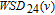 can be calculated as
can be calculated as
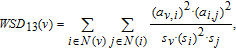 | (9) |
 | (10) |
where for each 4-cycle, the corresponding term of the sum is the product of edge weights divided by the product of node strengths.
However, it is extremely difficult to derive Eq. (10) in the WSSN model, because we cannot obtain the formula of
 for
for
 . In this paper, we decompose Eq. (10) into the sum over all 4-cycles associated with pattern 2
. In this paper, we decompose Eq. (10) into the sum over all 4-cycles associated with pattern 2
 and the sum over all 4-cycles associated with pattern 4
and the sum over all 4-cycles associated with pattern 4
 as follows:
as follows:
 | (11) |
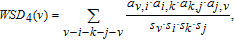 | (12) |
where
v-
i-
k-
j-
v denotes all 4-cycles associated with pattern 4.
As is well known, the WSD in weighted graph G can be expressed as
 | (13) |
5.
 in WSSN model
in WSSN modelFirst, we will further classify the nodes labeled as k (i.e., added at step
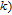 in
in
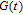 (see Section 2). Based on the construction rule of the WSSN model, each node k must be generated by an edge in
(see Section 2). Based on the construction rule of the WSSN model, each node k must be generated by an edge in
 and any edge with weight w in
and any edge with weight w in
 must generate
must generate
 nodes k. Thus, we define
nodes k. Thus, we define
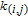 as a node k generated by edge
as a node k generated by edge
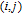 where
where
 . If
. If
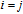 , both i and j must be zero, and if
, both i and j must be zero, and if
 , all of i, j, and k must be zero. Let
, all of i, j, and k must be zero. Let
 denote the number of all nodes
denote the number of all nodes
 .
.
Then, we can obtain the following theorem (see Appendix A for the proof).
Second, we will derive the formula of
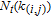 which is defined as a set of neighbors of node
which is defined as a set of neighbors of node
 in
in
 . As is well known,
. As is well known,
 includes only one node i and only one node j, and for
includes only one node i and only one node j, and for
 ,
,
 includes all nodes in
includes all nodes in
 and all nodes
and all nodes
 ,
,
 and
and
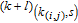 where
where
 and
and
 .
.
Thus,
 can be expressed as
can be expressed as
 | (14) |
where

only includes the nodes added at step
l of the WSSN model.
As is well known,
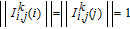 , where
, where
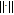 denotes the cardinality of a set.
denotes the cardinality of a set.
Additionally, according to the edges that generate nodes
 ,
,
 | (15) |
where
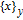
denotes a set composed of
y different nodes labeled as
x.
In
 , the weight of edge
, the weight of edge
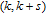 for
for
 is
is
 , and the weight of edges
, and the weight of edges
 and
and
 is
is
 . Because the number of edges
. Because the number of edges
 attached to node
attached to node
 is equal to
is equal to
 , we have
, we have
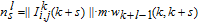 in Eq. (15). Moreover,
in Eq. (15). Moreover,
 and
and
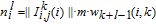 in Eq. (15).
in Eq. (15).
Thus, for
 , we can obtain
, we can obtain
 | (16) |
Based on Eq. (16),
 . Using
. Using
 , we can derive the following equations:
, we can derive the following equations:
 | (17) |
 | (18) |
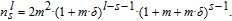 | (19) |
Third, we will derive
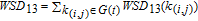 . According to Eq. (9), for each neighbor
. According to Eq. (9), for each neighbor
 , we need to derive its neighbor set
, we need to derive its neighbor set
 . Based on Eqs. (14) and (15), except for nodes in
. Based on Eqs. (14) and (15), except for nodes in
 and
and
 , the neighbor sets of all nodes in
, the neighbor sets of all nodes in
 are easy to derive. Thus, it is critical to investigate the generation process of edge
are easy to derive. Thus, it is critical to investigate the generation process of edge
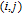 which generates node
which generates node
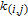 with
with
 (both i and j must be zero if
(both i and j must be zero if
 and all of i, j, and k must be zero if
and all of i, j, and k must be zero if
 .
.
Category 1 When
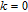 , both nodes i and j can be expressed as
, both nodes i and j can be expressed as
 , and the number of nodes
, and the number of nodes
 is
is
 (see Theorem 1).
(see Theorem 1).
Category 2 When
 , both nodes i and j can be expressed as
, both nodes i and j can be expressed as
 , and the number of nodes
, and the number of nodes
 is
is
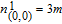 (see Theorem 1).
(see Theorem 1).
When
 , we analyze the following five categories:
, we analyze the following five categories:
Category 3 When
 and
and
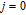 , both nodes i and j can be expressed as
, both nodes i and j can be expressed as
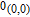 , and the number of nodes
, and the number of nodes
 is
is
 (see Theorem 1).
(see Theorem 1).
Category 4 When
 , node i can be expressed as
, node i can be expressed as
 , node j must be generated by an edge
, node j must be generated by an edge
 where
where
 , and the number of nodes
, and the number of nodes
 is
is
 . Additionally, each edge
. Additionally, each edge
 must generate
must generate
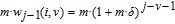 nodes j, and each edge
nodes j, and each edge
 must generate
must generate
 nodes k. Specifically, according to Eqs. (14) and (15), we can obtain
nodes k. Specifically, according to Eqs. (14) and (15), we can obtain
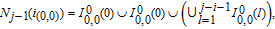 | (20) |
 | (21) |
Note that the intersection of two sets
 in Eq. (20) is null, because the two sets include different nodes that are marked as the same symbol.
in Eq. (20) is null, because the two sets include different nodes that are marked as the same symbol.
Categories 5, 6, and 7 When
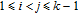 , we assume that the edge that generates node i is
, we assume that the edge that generates node i is
 where
where
 (both x and y must be zero if
(both x and y must be zero if
 . Then, node j must be generated by an edge
. Then, node j must be generated by an edge
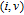 or
or
 where
where
 . Additionally, each edge
. Additionally, each edge
 or
or
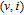 must generate
must generate
 nodes j, and each edge
nodes j, and each edge
 must generate
must generate
 nodes k.
nodes k.
Specifically, we can obtain
 | (22) |
 | (23) |
Now, we should further analyze the following three categories for nodes
 .
.
Category 8 When node i is generated by edge
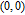 , the number of nodes
, the number of nodes
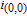 is
is
 (see Theorem 1).
(see Theorem 1).
Category 9 When node i is generated by edge
 where
where
 , the number of nodes
, the number of nodes
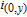 is
is
 (see Theorem 1).
(see Theorem 1).
Category 10 When node i is generated by edge
 where
where
 and
and
 , the number of nodes
, the number of nodes
 is
is
 (see Theorem 1).
(see Theorem 1).
According to the above analysis, we can determine the edges which generate the nodes in
 and
and
 . Thus, the neighbor set of each node in
. Thus, the neighbor set of each node in
 can be derived. Assume that node
can be derived. Assume that node
 is generated by edge
is generated by edge
 , i.e., nodes i and j are respectively generated by edges
, i.e., nodes i and j are respectively generated by edges
 and
and
 .
.
Then, based on Eqs. (1), (2), (9), (14), and (15), in weighted graph
 , we can derive the following equation:
, we can derive the following equation:
 | (24) |
The above analysis has classified nodes
 as seven categories: 1.
as seven categories: 1.
 ; 2.
; 2.
 ; 3.
; 3.
 and
and
 ; 4.
; 4.
 and
and
 ; 5.
; 5.
 and
and
 ; 6.
; 6.
 and
and
 ; 7. 2
; 7. 2
 and
and
 . For each category above, the edges
. For each category above, the edges
 and
and
 that respectively generate nodes i and j can be determined.
that respectively generate nodes i and j can be determined.
Thus, we expand
 as follows:
as follows:
 | (25) |
where


are the sums of

and respectively related to the above seven categories 1–7.
Specifically, we can obtain
 | (26) |
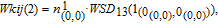 | (27) |
 | (28) |
 | (29) |
 | (30) |
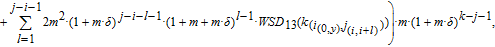 | (31) |
 | (32) |
Fourth, we will derive
 . According to Eq. (11), it is critical to extract all pairs of nodes in
. According to Eq. (11), it is critical to extract all pairs of nodes in
 for the calculation of
for the calculation of
 . Based on Eq. (14), the node pairs u and v can be classified as three cases as follows.
. Based on Eq. (14), the node pairs u and v can be classified as three cases as follows.
Case 1 For
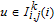 and
and
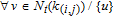 , the sum over 4-cycles associated with
, the sum over 4-cycles associated with
 can be expressed as
can be expressed as
 | (33) |
where for each 4-cycle, the corresponding term of the sum is the product of edge weights divided by the product of node strengths.
Case 2 For
 and
and
 , the sum over 4-cycles associated with
, the sum over 4-cycles associated with
 can be expressed as
can be expressed as
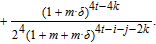 | (34) |
Case 3 For
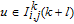 and
and
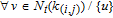 where
where
 , the sum over 4-cycles associated with
, the sum over 4-cycles associated with
 can be expressed as
can be expressed as
 | (35) |
Therefore, we can obtain
 | (36) |
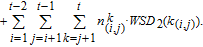 | (37) |
Fifth, we will derive
 . According to Eq. (12), we need to determine all 4-cycles of pattern 4 with start node
. According to Eq. (12), we need to determine all 4-cycles of pattern 4 with start node
 for calculating
for calculating
 . Using the schematic illustration shown in Fig. 3, we present seven cases for these 4-cycles as follows.
. Using the schematic illustration shown in Fig. 3, we present seven cases for these 4-cycles as follows.
Case 1 Assume that node j is generated by edge
 if
if
 where edge
where edge
 generates node i (or generated by edge
generates node i (or generated by edge
 if
if
 ,
,
 and
and
 are among these cases.
are among these cases.
An example of Case 1 in Fig. 3 is
 .
.
Case 2 For any node
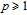 that is generated by edge
that is generated by edge
 and different from the start node
and different from the start node
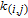 ,
,
 and
and
 are among these cases. An example of case 2 in Fig. 3 is
are among these cases. An example of case 2 in Fig. 3 is
 .
.
Case 3 Assume node
 , for any pair of nodes l and
, for any pair of nodes l and
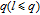 that are generated by edge
that are generated by edge
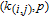 if
if
 (or edge
(or edge
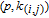 if
if
 ,
,
 and
and
 are among these cases.
are among these cases.
An example of Case 3 in Fig. 3 is
 .
.
Case 4 Assume that node
 and p is a node generated by edge
and p is a node generated by edge
 if
if
 (or edge
(or edge
 if
if
 , for any node q generated by edge
, for any node q generated by edge
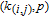 ,
,

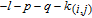 and
and
 are among these cases.
are among these cases.
An example of Case 4 in Fig. 3 is
 .
.
Case 5 Assume that node
 and q is a node generated by edge
and q is a node generated by edge
 if
if
 (or edge
(or edge
 if
if
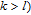 , for any node p generated by edge
, for any node p generated by edge
 ,
,
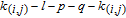 and
and
 are among these cases.
are among these cases.
An example of Case 5 in Fig. 3 is
 .
.
Case 6 For any node q that is generated by edge
 ,
,
 and
and
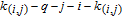 are among these cases.
are among these cases.
An example of Case 6 in Fig. 3 is
 .
.
Case 7 For any node q that is generated by edge
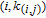 ,
,
 and
and
 are among these cases.
are among these cases.
An example of Case 7 in Fig. 3 is
 .
.
For start node
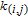 , the above cases 2–7 do not need to determine which edges generate nodes i and j where edge
, the above cases 2–7 do not need to determine which edges generate nodes i and j where edge
 generates the start node. Thus, it is easy to calculate
generates the start node. Thus, it is easy to calculate
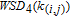 for these cases.
for these cases.
For Case 2, edge
 generates
generates
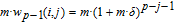 nodes p for
nodes p for
 , and
, and
 nodes p for
nodes p for
 . Thus, the corresponding
. Thus, the corresponding
 of this case can be expressed as
of this case can be expressed as
 | (38) |
where node strength

and edge weight

are defined in Eqs. (
1) and (
2).
For Case 3, based on Eq. (14), if
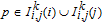 , the set of all nodes generated by edge
, the set of all nodes generated by edge
 is
is
 where
where
 denotes a set composed of
denotes a set composed of
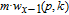 nodes that are added at step x. If
nodes that are added at step x. If
 where
where
 , the set of all nodes generated by edge
, the set of all nodes generated by edge
 is
is
 . Thus, the corresponding
. Thus, the corresponding
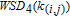 of this case can be expressed as follows:
of this case can be expressed as follows:
 | (39) |
Like the analyses of Cases 2 and 3, we can respectively derive the corresponding
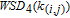 of Cases 4–7 as follows:
of Cases 4–7 as follows:
 | (40) |
 | (41) |
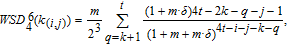 | (42) |
 | (43) |
It is worth noting that
 and
and
 in Eqs. (40)–(43) have been respectively substituted by Eqs. (1) and (eqs. (2)). Thus,
in Eqs. (40)–(43) have been respectively substituted by Eqs. (1) and (eqs. (2)). Thus,
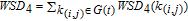 associated with Cases 2–7 can be expressed as follows:
associated with Cases 2–7 can be expressed as follows:
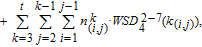 | (44) |
where
 | (45) |
For start node
 , Case 1 needs to determine which edges generate nodes i and j. Thus, we need to classify nodes
, Case 1 needs to determine which edges generate nodes i and j. Thus, we need to classify nodes
 as seven categories: 1.
as seven categories: 1.
 ; 2.
; 2.
 ; 3.
; 3.
 and
and
 ; 4.
; 4.
 and
and
 ; 5.
; 5.
 and
and
 ; 6.
; 6.
 and
and
 ; 7.
; 7.
 and
and
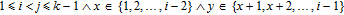 . This classification of nodes
. This classification of nodes
 has been analyzed in detail for the calculation of
has been analyzed in detail for the calculation of
 . Let
. Let
 denote the sum of
denote the sum of
 associated with Case 1, then, using a similar method for calculating WSD
13, we will be able to expand
associated with Case 1, then, using a similar method for calculating WSD
13, we will be able to expand
 as follows:
as follows:
 | (46) |
where


are the sums of
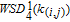
and respectively related to the above seven categories 1–7.
Specifically, we can obtain
 | (47) |
 | (48) |
 | (49) |
 | (50) |
 | (51) |
 | (52) |
 | (53) |
Thus, according to Eqs. (44) and (Eqs. (46)), we can obtain
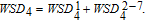 | (54) |
Finally, according to Eqs. (25), (Eqs. (37)), and (54), we can derive the WSD in
 as follows:
as follows:
 | (55) |
It is extremely complicated to manually express the WSD in
 with three parameters m, δ, and t. Fortunately, the Symbolic Math Toolbox of Matlab can help us to simplify the expression of the WSD. However, it is not intelligent enough for the toolbox to finish the work alone. For example, if we assume that
with three parameters m, δ, and t. Fortunately, the Symbolic Math Toolbox of Matlab can help us to simplify the expression of the WSD. However, it is not intelligent enough for the toolbox to finish the work alone. For example, if we assume that
 and
and
 , for functions
, for functions
 and
and
 , Matlab R2015a code
, Matlab R2015a code
 returns to
returns to
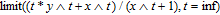 which is an invalid result, but
which is an invalid result, but
 can return to the expected result 1. Thus, we need to compile extra codes to deal with the transformation from φ to ψ.
can return to the expected result 1. Thus, we need to compile extra codes to deal with the transformation from φ to ψ.
Because the expression of the WSD is very long, according to Eq. (3), we only present the limit of the ratio of the WSD to the network order with
 as follows:
as follows:
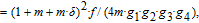 | (56) |
where
 | (57) |
 | (58) |
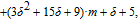 | (59) |
 | (60) |
 | (61) |
Therefore, the WSD grows sublinearly as the network order of the WSSN model increases. Additionally, it is easy to verify that both the partial derivatives of Eq. (56) with respect to m and δ are smaller than 0 for
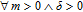 (because the expressions of the two partial derivatives are very long, we do not present the expressions in this paper, but we can use the “diff” function of Matlab to demonstrate these results). Thus, the limit of the ratio of the WSD to the network order monotonically decreases with increasing m and δ, i.e., the limit provides a sensitive discrimination for each input of the WSSN model.
(because the expressions of the two partial derivatives are very long, we do not present the expressions in this paper, but we can use the “diff” function of Matlab to demonstrate these results). Thus, the limit of the ratio of the WSD to the network order monotonically decreases with increasing m and δ, i.e., the limit provides a sensitive discrimination for each input of the WSSN model.
6. Applications in synthetic weighted networksThe mathematical derivation process of Section 5 demonstrates that the WSD is a good indicator to distinguish different weighted evolving systems. In this section, we choose three evolving weighted systems derived by classical Barrat’s model [33] to verify the applicability of the WSD. The model generates weighted networks based on growth and weights’ dynamics: at each time step, the model adds a new node and connects it to m previously existing nodes for the growth; also, for each of the m existing nodes, the model updates the weights of edges connected to the node and makes the node strength increased by δ. According to the study of Barrat et al.,[33]
 reflects the influence of newly added edges on the weight distribution where
reflects the influence of newly added edges on the weight distribution where
 denotes the initial weights of the newly added edges. As shown in Fig. 4, the WSD grows sublinearly as the network order of a certain weighted evolving system increases, that is, the ratio of the WSD to the network order remains stable for these networks with different orders. Furthermore, figure 44 shows that the ratio of the WSD to the network order can effectively distinguish different weighted evolving systems. Therefore, this study is important for promoting the WSD applicability in weighted evolving networks.
denotes the initial weights of the newly added edges. As shown in Fig. 4, the WSD grows sublinearly as the network order of a certain weighted evolving system increases, that is, the ratio of the WSD to the network order remains stable for these networks with different orders. Furthermore, figure 44 shows that the ratio of the WSD to the network order can effectively distinguish different weighted evolving systems. Therefore, this study is important for promoting the WSD applicability in weighted evolving networks.
7. ConclusionsWeighted, high and order-independent clustering coefficient and restricted power-law exponent falling in
 are features existing in most realistic evolving networks. In this paper, we rigorously investigate the WSD in the WSSN model which captures all of the mentioned features. In contrast to the unweighted model with zero clustering coefficient, the derivation of the WSD in the WSSN model is very complicated. However, with the help of the Symbolic Math Toolbox of Matlab, we demonstrate that the ratio of the WSD to the network order is asymptotically independent of the network order of the WSSN model and monotonically decreases as each input of the model increases. Furthermore, the rigorous derivation process of the WSD studied in this paper will provide a helpful insight into a understanding of the WSD in weighted network systems.
are features existing in most realistic evolving networks. In this paper, we rigorously investigate the WSD in the WSSN model which captures all of the mentioned features. In contrast to the unweighted model with zero clustering coefficient, the derivation of the WSD in the WSSN model is very complicated. However, with the help of the Symbolic Math Toolbox of Matlab, we demonstrate that the ratio of the WSD to the network order is asymptotically independent of the network order of the WSSN model and monotonically decreases as each input of the model increases. Furthermore, the rigorous derivation process of the WSD studied in this paper will provide a helpful insight into a understanding of the WSD in weighted network systems.
Appendix A: The proof of Theorem 1
As is well known, the number of nodes
 is 3. Thus,
is 3. Thus,
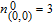 and Case A is correct.
and Case A is correct.
Based on Eq. (2), the weight of each edge
 in
in
 is
is
 . Thus,
. Thus,
 nodes k are generated by edge
nodes k are generated by edge
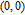 in
in
 when
when
 . There are 3 edges
. There are 3 edges
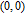 which induce that
which induce that
 if
if
 . Thus Case B is correct.
. Thus Case B is correct.
Using an induction method to prove Case C: when
 , j must be 1, and
, j must be 1, and
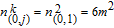 (i.e., Case C holds for k = 2 and
(i.e., Case C holds for k = 2 and
 .
.
Assume that Case C holds for

 and
and
 . When
. When
 ,
,
 is determined by the number of all edges
is determined by the number of all edges
 in
in
 (i.e.,
(i.e.,
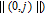 and the weight of edge
and the weight of edge
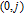 in
in
 (i.e.,
(i.e.,
 derived by Eq. (2)).
derived by Eq. (2)).
Edge
 is generated if and only if nodes
is generated if and only if nodes
 are added at step j of the WSSN model. Specifically,
are added at step j of the WSSN model. Specifically,
 generates only one edge
generates only one edge
 and
and
 generates two edges
generates two edges
 . Thus, we can obtain
. Thus, we can obtain
 | (A1) |
And according to the construction rule of the WSSN model,
 | (A2) |
According to the above assumption and Case B, we can derive the formulas of
 and
and
 . Furthermore, we can obtain
. Furthermore, we can obtain
 | (A3) |
Therefore, for
 and
and
 , Case C remains correct.
, Case C remains correct.
Using an induction method to prove Case D: when
 , i and j must be 1 and 2, respectively, and
, i and j must be 1 and 2, respectively, and
 (i.e., Case D holds for
(i.e., Case D holds for
 and
and
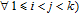 .
.
Assume that Case D holds for
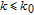
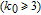 and
and
 . When
. When
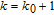 ,
,
 is determined by the number of all edges
is determined by the number of all edges
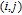 in
in
 (i.e.,
(i.e.,
 and the weight of edge
and the weight of edge
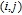 in
in
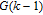 (i.e.,
(i.e.,
 derived by Eq. (2)).
derived by Eq. (2)).
Edge
 is generated if and only if nodes
is generated if and only if nodes
 ,
,
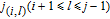 are added at step j of the WSSN model. Specifically, each node
are added at step j of the WSSN model. Specifically, each node
 or
or

 generates only one edge
generates only one edge
 . Thus, we can obtain
. Thus, we can obtain
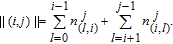 | (A4) |
And according to the construction rule of the WSSN model, we have
 | (A5) |
According to the above assumption and Case C, we can derive the formulas of
 ,
,
 and
and
 . Furthermore, we can obtain
. Furthermore, we can obtain
 | (A6) |
Therefore, for
 and
and
 , Case D remains correct.
, Case D remains correct.
Appendix B: The proof of Theorem 2
First of all, we extract two properties of weighted graph
 as follows.
as follows.
Property 1 For any node k (i.e., a node added at step
 with
with
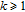 , if two different nodes i and j are connected with node k and
, if two different nodes i and j are connected with node k and
 ,
,
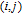 must be the only one edge that generates node k and edge
must be the only one edge that generates node k and edge
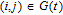 .
.
Property 2 For any node k with
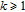 , if node i is attached to node k in
, if node i is attached to node k in
 , we can determine that
, we can determine that
 .
.
The above two properties can be easily confirmed by Eq. (14).
Proof We analyze the 4-cycle as shown in Fig. A1.
Without loss of generality, we assume
 .
.
If
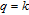 , then
, then
 due to Property 2. Because
due to Property 2. Because
 includes only three nodes 0, we can determine
includes only three nodes 0, we can determine
 . Thus, p is a node generated by edge
. Thus, p is a node generated by edge
 due to property 1, i.e., the 4-cycle belongs to Case 2.
due to property 1, i.e., the 4-cycle belongs to Case 2.
If
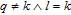 , then
, then
 and
and
 due to Property 2. If
due to Property 2. If
 , then
, then
 due to the assumption
due to the assumption
 , and edge
, and edge
 generates node p due to Property 1. Because
generates node p due to Property 1. Because
 , node q is generated by edge
, node q is generated by edge
 due to Property 1, i.e., the 4-cycle belongs to Case 5.
due to Property 1, i.e., the 4-cycle belongs to Case 5.
When
 :
:
1) if
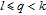 , then edge
, then edge
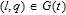 generates node
generates node
 due to Property 1. If
due to Property 1. If
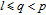 , then node p is generated by edge
, then node p is generated by edge
 , i.e., the 4-cycle belongs to Case 2. If
, i.e., the 4-cycle belongs to Case 2. If
 , then
, then
 due to Property 2. Thus, node q is generated by edge
due to Property 2. Thus, node q is generated by edge
 , i.e., the 4-cycle belongs to Case 1. Note that Case 2 requires
, i.e., the 4-cycle belongs to Case 1. Note that Case 2 requires
 . If
. If
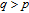 , then
, then
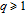 . Because
. Because
 and
and
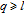 , node q is generated by edge
, node q is generated by edge
 , i.e., the 4-cycle belongs to Case 1.
, i.e., the 4-cycle belongs to Case 1.
2) if
 ,
,
 . Thus, edge
. Thus, edge
 generates node p due to Property 1. Because
generates node p due to Property 1. Because
 and
and
 ,
,
 and node q is generated by edge
and node q is generated by edge
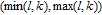 , i.e., the 4-cycle belongs to Case 5.
, i.e., the 4-cycle belongs to Case 5.
If
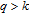 , then
, then
 and
and
 due to Property 2.
due to Property 2.
3) if
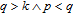 , then edge
, then edge
 generates node q due to Property 1. If
generates node q due to Property 1. If
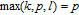 , then
, then
 (otherwise
(otherwise
 that is contradictive to the precondition
that is contradictive to the precondition
 . Because edge
. Because edge
 ,
,
 due to Property 2 and node p is generated by edge
due to Property 2 and node p is generated by edge
 due to Property 1, i.e., the 4-cycle belongs to Case 4. If
due to Property 1, i.e., the 4-cycle belongs to Case 4. If
 , then
, then
 and node l is generated by edge
and node l is generated by edge
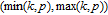 due to Property 1, i.e., the 4-cycle belongs to Case 3. If
due to Property 1, i.e., the 4-cycle belongs to Case 3. If
 , then
, then
 and
and
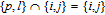 for node
for node
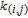 due to Property 1. Then, the 4-cycle belongs to Case 6 if
due to Property 1. Then, the 4-cycle belongs to Case 6 if
 , or belongs to Case 7 if
, or belongs to Case 7 if
 .
.