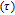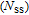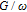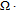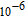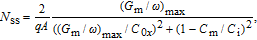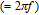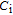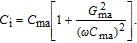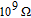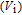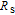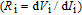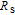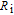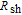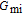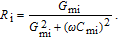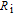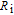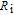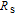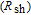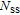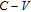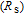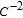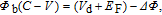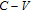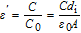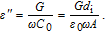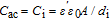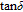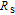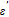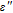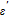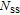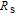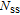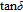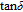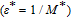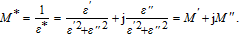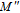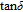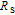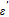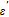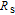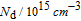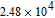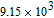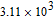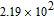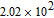1. IntroductionMetal–semiconductor (or Schottky) devices have been studied largely for years in order to obtain different application areas of these devices, such as low voltage rectifiers, inverters at high frequency, polarity protection and freewheeling diodes.[1–5] In the recent years, they have aroused the researchers’ interest in optical and electronic devices.[6–8] For these reasons, these devices should be investigated with different semiconductors or polymers in the interface materials. Already, in this area, researchers investigated new material Schottky devices because they wanted to gain new generation Schottky devices.[9–12] In this respect, here, in the present work, the effect of zinc oxide (ZnO) interfacial layer on electrical and dielectric properties are investigated because it has high direct band gap (3.37 eV), high exciton binding energy (~ 60 meV), very promising properties like that low costs, non-toxicity and low temperature deposition.[13–16] ZnO also has many application areas such as Schottky barrier diodes (SBDs) solar cells (SCs), chemical sensors (CSs), light-emitting diodes (LEDs), UV and laser diodes (LDs).[17–22]
Dielectric characterization of this device helps to understand conduction and polarization mechanism which can be divided into four parts according to magnitude of applied frequency; electronic, ionic, dipolar, and surface polarizations.[23] Oriental non-dipole polarization usually can be seen in intermediate or high frequency range (
 Hz–
Hz–
 Hz) due to long relaxation time
Hz) due to long relaxation time
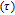 . This polarization can be based on existence of constant orientable dipoles, surface charges and impurities.[24] To know more information about polarization and conductions mechanisms, the real and imaginary parts of complex dielectric constant
. This polarization can be based on existence of constant orientable dipoles, surface charges and impurities.[24] To know more information about polarization and conductions mechanisms, the real and imaginary parts of complex dielectric constant
 and AC electrical conductivity
and AC electrical conductivity
 should be studied in large ranges frequency and voltage. In this way, the more trustworthy and correctly experimental results can be acquired.[25]
should be studied in large ranges frequency and voltage. In this way, the more trustworthy and correctly experimental results can be acquired.[25]
There are two main aims in this study: the first one is to best understand the effects of interface states
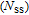 or interface traps
or interface traps
 with different lifetimes, ZnO interfacial layers, and polarizations on the electrical and dielectric characterization of Au/ZnO/n–Si devices depending on various parameters such as frequency, applied bias voltage, series resistance, interfacial layer, and barrier height (BH) inhomogeneity. The second aim is to fill in this area since dielectric properties of ZnO/n–Si did not studied in literature. Therefore, both the capacitance–voltage
with different lifetimes, ZnO interfacial layers, and polarizations on the electrical and dielectric characterization of Au/ZnO/n–Si devices depending on various parameters such as frequency, applied bias voltage, series resistance, interfacial layer, and barrier height (BH) inhomogeneity. The second aim is to fill in this area since dielectric properties of ZnO/n–Si did not studied in literature. Therefore, both the capacitance–voltage
 and conductance–voltage
and conductance–voltage
 measurements of this device is performed in the wide ranges of frequency and voltage at room temperature. The values of
measurements of this device is performed in the wide ranges of frequency and voltage at room temperature. The values of
 and
and
 , real and imaginary parts of complex electric modulus
, real and imaginary parts of complex electric modulus
 , loss tangent
, loss tangent
 ,
,
 are obtained by using the measured
are obtained by using the measured
 and
and
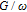 which are dependented on frequency and applied bias voltage.
which are dependented on frequency and applied bias voltage.
3. Results and discussionIt could be understood that the device behaviors are obtained based on the investigations of
 and
and
 because they strongly influence electrical properties.[26] Correlation of
because they strongly influence electrical properties.[26] Correlation of
 with frequency is obtained by Hill–Coleman technique for ZnO/n–Si device. According to this method, the voltage dependence of
with frequency is obtained by Hill–Coleman technique for ZnO/n–Si device. According to this method, the voltage dependence of
 can be expressed as following relation:[25]
can be expressed as following relation:[25]
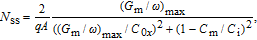 | (1) |
where
A is the Schottky contact area,

is the angular frequency
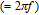
,

is the peak value of capacitance, and

is corresponding to its peak value,
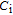
is the interfacial insulator layer capacitance obtained from following equation at strong accumulation region
[27–29]
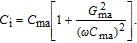 | (2) |
Usually, the sources of series resistances
 in electronic devices such as MS, MIS (metal–insulator–semicondcutor) and solar cells are the contact made of the probe wire to the gate, the back contact to the semiconductor, particulate matter between the back contact and the pedestal, the resistance of the quasi-neutral bulk of the semiconductor and an extremely non-uniform doping distribution of donor or acceptor atoms in the semiconductor.[29] On the other hand, the value of shunt resistances
in electronic devices such as MS, MIS (metal–insulator–semicondcutor) and solar cells are the contact made of the probe wire to the gate, the back contact to the semiconductor, particulate matter between the back contact and the pedestal, the resistance of the quasi-neutral bulk of the semiconductor and an extremely non-uniform doping distribution of donor or acceptor atoms in the semiconductor.[29] On the other hand, the value of shunt resistances
 may originate from a leakage oxide, leakage current paths along the interlayer and shunt paths from the probe wire to the ground. Therefore, to determine the performances and quality of these semiconductor devices, both series and shunt resistances (
may originate from a leakage oxide, leakage current paths along the interlayer and shunt paths from the probe wire to the ground. Therefore, to determine the performances and quality of these semiconductor devices, both series and shunt resistances (
 and
and
 ) of these devices are very important which are expected to be zero and greater than
) of these devices are very important which are expected to be zero and greater than
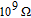 in the ideal case, but the application situation is considerably different from the ideal case. The structure resistance
in the ideal case, but the application situation is considerably different from the ideal case. The structure resistance
 is a function of applied bias voltage
is a function of applied bias voltage
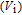 , but the real values of
, but the real values of
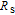 for these devices correspond to high enough forward bias voltages or strong accumulation region. The values of
for these devices correspond to high enough forward bias voltages or strong accumulation region. The values of
 for the MS and MIS types become more effective in the high forward bias voltage
for the MS and MIS types become more effective in the high forward bias voltage
 , leading to a concave curvature or bending of the forward bias
, leading to a concave curvature or bending of the forward bias
 plot in an accumulation region. Similarly, the value of
plot in an accumulation region. Similarly, the value of
 also leads to a deviations from linearity in the semi-logarithmic forward bias
also leads to a deviations from linearity in the semi-logarithmic forward bias
 plots of these devices. In addition, there are many methods in the literature to determine the value of
plots of these devices. In addition, there are many methods in the literature to determine the value of
 such as Cheung, Norde and Nicollian–Brews methods, but the value of
such as Cheung, Norde and Nicollian–Brews methods, but the value of
 may be different from method to method due to the nature of measured system and applied bias or current range.[27–29] Among these methods, Ohm’s law
may be different from method to method due to the nature of measured system and applied bias or current range.[27–29] Among these methods, Ohm’s law
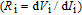 and Nicollian–Brews methods are very suitable and reliable to determine
and Nicollian–Brews methods are very suitable and reliable to determine
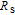 values of these devices by using forward bias current–voltage
values of these devices by using forward bias current–voltage
 and impedance measurement plots (
and impedance measurement plots (
 and
and
 , respectively, with respect to time consumption, easiness and quickness. In other words,
, respectively, with respect to time consumption, easiness and quickness. In other words,
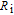 is the structure resistance as a function of applied bias voltage
is the structure resistance as a function of applied bias voltage
 , but the real values of
, but the real values of
 and
and
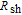 for these devices correspond to high enough forward bias voltage or strong accumulation region and low enough reverse bias voltages or strong inversion region, respectively.
for these devices correspond to high enough forward bias voltage or strong accumulation region and low enough reverse bias voltages or strong inversion region, respectively.
The voltage and frequency dependent profile of resistance
 can also be determined from the measured values of capacitance and conductance (
can also be determined from the measured values of capacitance and conductance (
 and
and
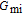 ) measurements for each frequency, but the real value of it corresponding to the strong accumulation region at enough high frequency (
) measurements for each frequency, but the real value of it corresponding to the strong accumulation region at enough high frequency (
 500 kHz) by using Nicollian and Brews method through using the following relation[29]
500 kHz) by using Nicollian and Brews method through using the following relation[29]
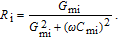 | (3) |
The voltage-dependent
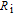 profiles for various frequencies are shown in Fig. 1. It could be seen in this figure that
profiles for various frequencies are shown in Fig. 1. It could be seen in this figure that
 values are constant in the inversion and accumulation region, but there are peaks in depletion region for almost all frequencies. However, intensities of peaks decrease with frequencies increasing from 10 kHz to 1 MHz. This situation could be explained that interface states become effective at low frequencies.
values are constant in the inversion and accumulation region, but there are peaks in depletion region for almost all frequencies. However, intensities of peaks decrease with frequencies increasing from 10 kHz to 1 MHz. This situation could be explained that interface states become effective at low frequencies.
On the other hand,
 has peaks in the depletion region and peak positions change to forward bias with increasing frequency due to a special density distribution of
has peaks in the depletion region and peak positions change to forward bias with increasing frequency due to a special density distribution of
 at ZnO/n–Si and restructure and their reordering under action of electric field.[27,28] The values of
at ZnO/n–Si and restructure and their reordering under action of electric field.[27,28] The values of
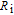 for high frequencies and forward bias voltages (accumulation region) are almost independent of voltage, and so they are for intermediate and higher frequencies.
for high frequencies and forward bias voltages (accumulation region) are almost independent of voltage, and so they are for intermediate and higher frequencies.
In a strong accumulation region
 the real value of
the real value of
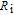 correspond to real value of series resistance
correspond to real value of series resistance
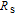 , but the maximum value of
, but the maximum value of
 at high reverse bias
at high reverse bias
 corresponds to the real value of shunt resistance
corresponds to the real value of shunt resistance
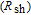 .[25]
.[25]
 value is discussed by changing frequency in the next part of this study.
value is discussed by changing frequency in the next part of this study.
Such frequency and voltage dependence values of
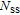 and
and
 are demanded that special attention is paid to their effects in the application of
are demanded that special attention is paid to their effects in the application of
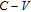 and
and
 characteristics. The frequency dependent profiles of
characteristics. The frequency dependent profiles of
 and
and
 (at 2 V) for Au/ZnO/n–Si device are calculated from
Eqs. (1) and (3), respectively, and shown in Fig. 2. The values of
(at 2 V) for Au/ZnO/n–Si device are calculated from
Eqs. (1) and (3), respectively, and shown in Fig. 2. The values of
 and
and
 (at zero and 2 V) changing with frequency are also listed in Table 1. According to the plots of
(at zero and 2 V) changing with frequency are also listed in Table 1. According to the plots of
 and
and
 versus frequency of Au/ZnO/n–Si device, they increase at low frequencies, which can be attributed to the fact that they follow alternating current (AC) signal at those frequencies, but at high frequencies, they have decreasing tendency because the charges at traps cannot follow the AC signal.[28]
versus frequency of Au/ZnO/n–Si device, they increase at low frequencies, which can be attributed to the fact that they follow alternating current (AC) signal at those frequencies, but at high frequencies, they have decreasing tendency because the charges at traps cannot follow the AC signal.[28]
Table 1
Table 1
 | Table 1
Some electrical parameters of Au/ZnO/n–Si device at various frequencies.
. |
The values of intercept or diffusion potential
 and
concentration of donor atoms
and
concentration of donor atoms
 are obtained from the intercept and slope of the straight line part of 1/
are obtained from the intercept and slope of the straight line part of 1/
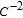 versus V plots for all measured
frequencies, respectively.[30] The values of barrier height (BH) with changing frequency could be obtained from the following formula:
versus V plots for all measured
frequencies, respectively.[30] The values of barrier height (BH) with changing frequency could be obtained from the following formula:
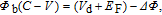 | (4) |
where

is the Fermi energy level and

is the image force BH lowering obtained from reverse bias
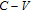
measurements, and it is negligibly small for intermediate doping concentration of semiconductor. As shown in Fig.
3, barrier height values generally decrease (first linear) down to 500 kHz then increased (second linear) with increasing frequency, but

values decrease with increasing frequency which is attributed to the fact that the electric charges are located in surface states and cannot follow an external AC signal at enough high frequencies. These cases can also be attributed to the particular distribution of

and its relaxation time and inhomogeneity of interlayer.
[28] The surface and dipole polarization are also more effective on the

and

characteristics, and so the electric and dielectric properties can be discussed at low and intermediate frequencies.
The complex permittivity of dielectric material can be obtained from the following relation:
 | (5) |
where

and

are called sequentially real and imaginary components of complex dielectric constant

, j is the imaginary root,
C and
G are the measured real and imaginary component of impedance
(Z) or admittance

respectively, and

is the capacitance of free capacitor. So, both the values of

and

can be determined from the values of
C and
G by using following relations
[24]
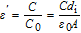 | (6) |
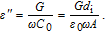 | (7) |
Here,
A is the contact area of device,

is the thickness of interlayer, and

is the permittivity of vacuum. Maximum capacitance value at enough high forward biases is corresponding to interlayer capacitance, and written as
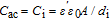
. The loss tangent

can be given as follows:
 | (8) |
Plots of dielectric constant, dielectric loss, and
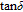 versus voltage of ZnO/n–Si device are shown in Figs. 4(a)–4(c), respectively for frequency changing from 10 kHz to 1 MHz. There are two peaks at low frequencies which are corresponding to depletion and accumulation regions but at high frequencies, only one peak appears with increasing frequency in Fig. 4(a). While the first peak can be attributed to the particular density distribution of
versus voltage of ZnO/n–Si device are shown in Figs. 4(a)–4(c), respectively for frequency changing from 10 kHz to 1 MHz. There are two peaks at low frequencies which are corresponding to depletion and accumulation regions but at high frequencies, only one peak appears with increasing frequency in Fig. 4(a). While the first peak can be attributed to the particular density distribution of
 , the second peak can be attributed to
, the second peak can be attributed to
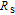 and interfacial layer. It can be seen from this figure that the values of
and interfacial layer. It can be seen from this figure that the values of
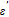 and
and
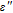 are a strong function of voltage and frequency at higher and intermediate bias voltage but they remain almost constant at low bias voltages (inversion region). The values of
are a strong function of voltage and frequency at higher and intermediate bias voltage but they remain almost constant at low bias voltages (inversion region). The values of
 and
and
 decrease with increasing frequency, which is attributed to the fact they cannot follow AC signal at high frequency because there is no so long time to orient the direction of the AC signal.[31] In other words, low values of
decrease with increasing frequency, which is attributed to the fact they cannot follow AC signal at high frequency because there is no so long time to orient the direction of the AC signal.[31] In other words, low values of
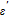 and
and
 are the results of the polarization processes and surface states and both of them decrease with increasing frequency since
are the results of the polarization processes and surface states and both of them decrease with increasing frequency since
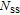 cannot follow an AC signal sufficiently at high frequencies.
cannot follow an AC signal sufficiently at high frequencies.
 and
and
 each reach a constant value at high frequencies (which can be seen in Fig. 1).[32]
each reach a constant value at high frequencies (which can be seen in Fig. 1).[32]
The plots of tangent loss
 versus voltage of Au/ZnO/n–Si device shows that
versus voltage of Au/ZnO/n–Si device shows that
 increases with increasing frequency as indicated in Fig. 4(c). It can be seen from this figure that there are no changes at forward bias or in depletion and accumulation regions, but at reverse bias
increases with increasing frequency as indicated in Fig. 4(c). It can be seen from this figure that there are no changes at forward bias or in depletion and accumulation regions, but at reverse bias
 values increase with increasing frequency up to
400 kHz then decrease to 1-MHz frequency. These changes of
values increase with increasing frequency up to
400 kHz then decrease to 1-MHz frequency. These changes of
 value can be attributed to the changes of polarization at AC signals.[30]
value can be attributed to the changes of polarization at AC signals.[30]
The plots of dielectric constant, dielectric loss, and
 versus frequency of ZnO/n–Si device for different voltages are shown in Figs. 5(a)–5(c), respectively for different voltages changing from 1 V to 2 V in steps of 0.25 V. As shown in these figures, the values of
versus frequency of ZnO/n–Si device for different voltages are shown in Figs. 5(a)–5(c), respectively for different voltages changing from 1 V to 2 V in steps of 0.25 V. As shown in these figures, the values of
 and
and
 (the inset shows closer views in Fig. 5(b)) both decrease with increasing frequency and voltage, which can be attributed to the
(the inset shows closer views in Fig. 5(b)) both decrease with increasing frequency and voltage, which can be attributed to the
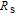 ,
,
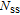 , and thickness of interlayer ZnO.[33]
, and thickness of interlayer ZnO.[33]
Plots of
 versus frequency of Au/ZnO/n–Si device for different voltages are shown in Fig. 5(c). As shown in this figure, the value of
versus frequency of Au/ZnO/n–Si device for different voltages are shown in Fig. 5(c). As shown in this figure, the value of
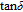 initial increases with increasing frequency for lower voltages then decreases with increasing frequency. This case can be attributed to the fact that the surface states and dipoles have no more time for orienting the direction of the AC electric field.[34] Furthermore,
initial increases with increasing frequency for lower voltages then decreases with increasing frequency. This case can be attributed to the fact that the surface states and dipoles have no more time for orienting the direction of the AC electric field.[34] Furthermore,
 values decrease from depletion regions to accumulation regions with increasing voltage.
values decrease from depletion regions to accumulation regions with increasing voltage.
The complex dielectric constant
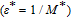 data are changed into the complex electric modulus formula
data are changed into the complex electric modulus formula
 by using the following equation to find real and imaginary electric modulus:[24]
by using the following equation to find real and imaginary electric modulus:[24]
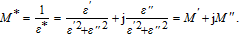 | (9) |
The values of
 and
and
 of the device are found to be strong functions of voltage and frequency. As shown in Fig. 6(a), the value of
of the device are found to be strong functions of voltage and frequency. As shown in Fig. 6(a), the value of
 increases with increasing frequency in inversion and depletion regions but it becomes independent of frequency especially in the accumulation region. Figure 6(b) shows that
increases with increasing frequency in inversion and depletion regions but it becomes independent of frequency especially in the accumulation region. Figure 6(b) shows that
 plots have peaks and the positions of these peaks shift towards the accumulation region with increasing frequency. These conclusions could be attributed to the particular distribution of the charges in the surface states and their relaxation times.[10]
plots have peaks and the positions of these peaks shift towards the accumulation region with increasing frequency. These conclusions could be attributed to the particular distribution of the charges in the surface states and their relaxation times.[10]
The plots of values of
 and
and
 versus frequency of device are shown in Figs. 7(a) and 7(b) for different low bias voltages, respectively. It can be seen from these figures that the values of
versus frequency of device are shown in Figs. 7(a) and 7(b) for different low bias voltages, respectively. It can be seen from these figures that the values of
 decrease with increasing biases because of removal electrode polarization, and the peaks are located at about 500-kHz frequency. Intensities of these peaks decrease with voltage increasing from 1 V to 2 V, which is attributed to a frequency-dependent dielectric relaxation.[31]
decrease with increasing biases because of removal electrode polarization, and the peaks are located at about 500-kHz frequency. Intensities of these peaks decrease with voltage increasing from 1 V to 2 V, which is attributed to a frequency-dependent dielectric relaxation.[31]
 values, which indicates that the energy loss of device decreases with increasing voltage.
values, which indicates that the energy loss of device decreases with increasing voltage.
The value of AC electric conductivity
 can be calculated from the following equation:
can be calculated from the following equation:
 | (10) |
The AC electric conductivity changing with voltage at different frequencies and changing with frequency at different voltages of Au/ZnO/n–Si device are shown in Figs. 8(a) and 8(b), respectively. As can be seen in Fig. 8(a), all
 plots have peaks at different frequencies in accumulation regions and increase with increasing frequency, positions of peaks shift towards high forward bias. In Fig. 8(b), AC electric conductivity is enhanced with increasing frequency and voltage. This increase in
plots have peaks at different frequencies in accumulation regions and increase with increasing frequency, positions of peaks shift towards high forward bias. In Fig. 8(b), AC electric conductivity is enhanced with increasing frequency and voltage. This increase in
 leads to the increase of eddy current which in turn increases the energy
leads to the increase of eddy current which in turn increases the energy
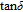 .[35] This increase in
.[35] This increase in
 can be attributed to reducing the series resistance and polarizations.[24,34,36,37]
can be attributed to reducing the series resistance and polarizations.[24,34,36,37]