† Corresponding author. E-mail:
We have investigated the photon-assisted shot noise properties in the magnetic field tunable heterostructures. Transport properties of the model structure are strongly dependent on the oscillatory field and the magnetic field. In this structure, electrons can absorb or emit one or multi-photons to reach the quasi-bound state. As a result, the transmission properties are affected considerably by photon-assisted tunneling and these features cause the nontrivial variations in the shot noise and Fano factor. It is found that the shot noise becomes spin-dependent and can be modulated not only by the magnetic field, but also by the oscillatory field. Both the spin-up and spin-down components of the shot noise can be greatly suppressed by the magnetic field, and can also be drastically enhanced by the harmonically driven field. Furthermore, with increasing external magnetic field, it is important to note that the enhanced intensity is decreased, even suppressed. These results suggest another method to suppress the shot noise via modulating the oscillatory field at a diluted-magnetic semiconductors/semiconductor structure.
Recently photon-assisted tunneling (PAT) in nanodevices has attracted considerable attention due to its potential applications in highly sensitive detectors, high-frequency radiation sources,[1,2] and solid-state quantum bit design.[3,4] PAT usually leads to Fano resonance, which is induced by the interference effect between localized states and the continuum band. Many theoretical approaches have been applied to the calculation of PAT in time-dependent structures.[1,2] Wagner and Zwerger have applied a Fabry–Perot method to study the characteristic scaling parameter of single driven barriers in a driven double-barrier structure.[3] They found an analytic expression for the characteristic scaling parameter of the photonic sidebands that exhibited a strong dependence on the spatial behavior of a driven potential. Using the transfermatrix technique, Wagner presented tunneling spectrum of a strongly driven double-well structure.[4] In his work, transport properties and quasienergy spectrum have been found to obey completely different scaling laws in the very same structure; Perez del Valle et al. researched the field-assisted tunneling in double-barrier with an oscillatory field and gave clear evidence that some drastic changes in the transmissivity occur either when the coupling to the field increases, or the frequency decreases;[5] Nie et al. investigated spin-dependent electron transmission through a quantum well[6] and a double-barrier[7] structure. In both cases, a multiplet structure in the transmission spectrum appeared and split into two sets due to the multiphoton process. Tang et al. used a Green’s function approach to investigate PAT through three quantum dots with spin–orbit coupling.[8] Using the Keldysh nonequilibrium Green’s function method, Yuan et al. theoretically studied the terahertz PAT in a quantum dot.[9] Some of their ideas for PAT are very much inspired by the terahertz PAT experiment.[10] Their results showed that, to observe the interesting photon-induced excited state resonance in InAs QD, the Coulomb interaction should be larger than the THz photon frequency.
The Mn-based diluted-magnetic-semiconductor (DMS) are prospective candidates for the materials that combine semiconductor behaviors with robust magnetism in application to spintronics devices. II–VI semiconductor low-dimensional structures based on DMS provided us an additional way to optimize the transport properties by using the external electric and magnetic field. The exploration of DMS has been developed since the pioneering work of Gaj et al. [11] and Douglas et al. [12] After that many creative theoretical and experimental works have been conducted to exploit spin-dependent phenomena. Egues[13] investigated electronic spin filtering in a magnetic-field tunable ZnSe/Zn1−x Mn x Se heterostructure and found strong spin-filtering effect. Guo et al. [14–18] have demonstrated several effects in such DMS systems, such as, spin-dependent suppression and enhancement, the electric effect, spin splitting effect. Zhu et al. [19] investigated the size dependence of spin-polarized transport through ZnSe/Zn1−x Mn x Se multi-layer structure and found that the polarization of current density can be reversed in a certain range of magnetic field. While most of the research in this field focus on the time-averaged quantities, relatively less to study the time-dependent properties, such as shot-noise. Shot noise, a non-equilibrium current fluctuation due to the quantization of the charge, is useful to obtain information on a system which is not available through conductance measurements.[20–22] Shot noise is the zero frequency limit of noise power when the bias voltage is sufficiently larger than the thermal energy. For an uncorrelated Poissonian process, the classical shot noise is given by the Schottky formula.[23] In the presence of spin-orbit coupling, the spin degeneracy is lifted so that the spin-up and spin-down electrons present very different transmission. Mishchenko studied shot noise in a system of diffusive ferromagnetic-paramagnetic-ferromagnetic spin valve.[24] Egues et al. [25,26] investigated shot noise for spinpolarized currents and entangled electron pairs with spin–orbit coupling in a four-probe geometry and found that shot noise exhibits Rashba-induced oscillations with continuous bunching and antibunching.
Motivated by these investigation, in this paper, we study photon-assisted shot noise in a time-dependent DMS/semiconductor heterostructure (ZnSe/Zn1−x Mn x Se) in the presence of both electric and magnetic fields. The results indicate that the shot noise can be significantly modulated by the oscillatory potential as well as the electric and magnetic fields.
We consider an oscillatory field and magnetic-field tunable three-barrier (for spin-up electron) or three-well (for spin-down electron) structure, shown in Fig. 



Here V 1 cos(ωt) is an oscillatory potential with the amplitude V 1 and the frequency ω.
Using the Floquet theorem,[28,29] the spin-dependent wave functions in the time-dependent structure can be written as:
Here ρ = (x,y) is the transverse coordinate, k xy is the in-plane wave vector of the transport electrons, the Floquet wave vectors
and J n (x) are the n-th order Bessel functions.
Within the framework of single electron approximation, using the transfer-matrix technique, the total Floquet transmission probability is given as follows:
In this paper, with uniform oscillating potential, both the spatial symmetry and time-reversal symmetry are present in the system, thus no pumped current exists at no temperature bias between the left and right electrodes. The spin-dependent current density through the magnetic-field tunable ZnSe/Zn1−x Mn x Se heterostructures is given by
where f l = f [E z +(n+1/2)ħω c], f r = f [E z +(n+1/2)ħω c + eV a], f is the Fermi distribution function, V a is the bias voltage applied to this structure, and J 0 = e2 /4π 2ħ2.
Using the Floquet scattering matrix,[30] in the low-frequency limit, the spin-dependent shot noise spectral density can be written as follows:
Throughout this paper we use 
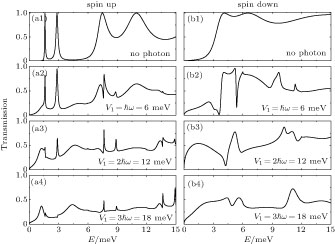
In Fig.
Figure
Figure
Furthermore, the dependence of the shot noise on the photon energy is nontrivial. From Fig.
To have a deeper insight into the influence induced by the photon energy, we investigated the Fano factor properties with the different the photon energy. In Fig.
In order to understand the sensitivity to the intensity of the oscillatory field, we plot the spin-dependent shot noise and Fano factor with different intensities in Figs.
From Fig.
In Fig.
We have investigated the photoassisted shot noise properties associated with spin-dependent tunneling in a DMS/semiconductor structure by using the Floquet theorem and the effective-mass approximation theory. The interplay of the multi-layer structure and the photon-assisted transmission processes plays an important role in the transport properties of the model structure. Electrons can absorb or emit one or multiple photons to reach the new path introduced by photon-assisted resonant path. As a result, the transmission properties are strongly dependent on the oscillatory field. These features cause the nontrivial variations in the shot noise and Fano factor. At moderate oscillatory field strength and frequency, suppression of the shot noise can be found. Our results suggest another method to suppress the shot noise via measuring the photon-assisted shot noise at a DMS/semiconductor structure.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] |