† Corresponding author. E-mail:
With hydrogen-like impurity (HLI) located in the center of CsI quantum pseudodot (QPD) and by using the variational method of Pekar type (VMPT), we investigate the first-excited state energy (FESE), excitation energy and transition frequency of the strongly-coupled bound polaron in the present paper. Temperature effects on bound polaron properties are calculated by employing the quantum statistical theory (QST). According to the present work’s numerical results, the FESE, excitation energy and transition frequency decay (amplify) with raising temperature in the regime of lower (higher) temperature. They are decreasing functions of Coulomb impurity potential strength.
The rapid developments in nano-material science and technology have led to the production of low-dimensional quantum structures called quantum dots (QDs).[1] Specifically, QDs are artificial atoms in which electrons are confined in the different potentials. Over the past thirty years, it has been shown theoretically and experimentally that the interaction between electrons and LO-phonons (e-LO-p) is in a strong coupling regime due to electronic energy levels in various material QDs. Many experiments performed on QDs involve energy levels rather than transition between the levels dealing with interaction between e-LO-p from the polarons in the QDs. For instance, by pump-probe mid-infrared spectroscopy, Sauvage et al. [2] investigated the dynamics of a polaron in the self-assembled n-doped InAsGaAs QDs. The long T1 decay time of the polaron was measured at both low temperature and room temperature, and its values were around 70 ps and 37 ps. Under optical pumping, and to achieve inter-sublevel population inversion, optical gain, and inter-sublevel polaron laser effect, Sauvage and Boucaud[3] proposed a three-level scheme in self-assembled n-doped InAs/GaAs QDs. Due to electron– phonon (ep) interactions (from polarons), Xu et al. [4] studied the mechanisms of quantum dissipation and broadening in self-formed InGaN QDs. The research discovered that a dissipative thermal bath embedded in the QDs is important for photon emission processes. Using the model of multimode Brownian oscillator, it set spontaneous emission spectra model and agreed with experiment and theory in the range of wide temperature. The impurity and the defect usually exist in real crystals. The properties of the crystals can be greatly influenced due to the existence of the impurity and the defect. Zhang et al. [5] investigated the effect of topological defects on the transport properties of a narrow ballistic ribbon of graphene with zigzag edges. Zhang and Hu et al. [6] found a Kosterlitz– Thouless type metal-to-insulator transition as a function of disorder strength or Fermi energy in disordered graphene with strong long-range impurities. By using a variational method of Pekar type, the Fermi Golden Rule and the quantum statistics theory, we investigate the effects of the hydrogen-like impurity and temperature on the coherence time of a parabolic QD qubit with a hydrogen-like impurity at the center.[7] Furthermore, in theories, by the method of Lee–Low–Pines (LLP) unitary transformation and the VMPT, Khordad[8] derived the expression of bound polaron under Rashba effect in a QPD. Using iterative and compact-density-matrix methods, Khordad[9] also obtained strongly-coupled impurity bound polaron in a QPD. Li et al. [10] studied polaron effects on optical absorption coefficients and refractive index changing in the 2D QPD system. From this theoretical research, the polaron properties were studied in various QDs with pseudoharmonic potential (PHP) that includes the harmonic and antidot potentials. Xiao[11] employed the VMPT to study magnetic field effect on RbCl QPD qubit. Sun et al. [12] investigated phonons’ effects in RbCl QPD qubit. Previous study of the most important polarons in QPD focused on the calculation of polarons state energies at zero temperature. Actually, the experiments for the state energies in physical system are performed at finite temperature, and consider that finite temperature is significant. Therefore it is very important to investigate the polaron state energies’ temperature effect. Using the QST, Chen et al. [13,14] investigated the effect of temperature on the probability density of the electron in parabolic QD qubit and the parabolic linear bound potential and Coulomb bound potential QD qubit. Li et al. [15] employed the same method to study the effect of temperature on magnetopolaronic vibrational frequency in an anisotropic QD. Sun et al. [16] studied the temperature effect on the FESE and transition frequency of a strongly-coupled polaron in symmetrical RbCl QD by using linear combination operator and the QST. For more information about temperature and polarons see the reference listed in Refs. [17]–[19]. However, the temperature effects on the strongly-coupled bound polaron properties in a CsI QPD have not been studied by employing the VMPT and QST so far.
In the present article, we thoroughly investigate the temperature effects and Coulomb impurity potential strength on the strongly-coupled bound polaron properties in CsI QPD with VMPT and QST. The research results have important theoretical significance, and are useful and meaningful for the implementation of low-dimensional quantum devices.
Considering a QPD of CsI crystal in the presence of electron-bulk longitudinal optical (LO) phonon interaction, an electron is bound to a HLI in the system, and is subjected to a pseudoharmonic potential (PHP). Within the framework of effective mass approximation, the Hamiltonian of the electron– phonon system takes the following form of
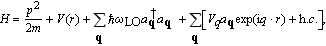 | (1) |
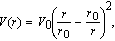 | (2) |
According to the VMPT[22,23] and the Ref. [24], the trial wavefunction is given by
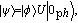 | (3) |
With 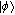
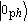
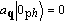

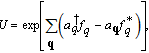 | (4) |
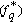
 | (5) |
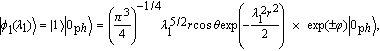 | (6) |
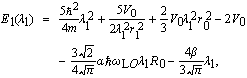 | (7) |
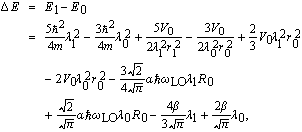 | (8) |
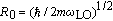
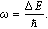 | (9) |
The LO phonons’ mean number around the electron can be described as
 | (10) |
At finite temperature and with HLI in the center of the CsI QPD, the different states’ statistical average value can be described by the strongly-coupled bound polaron properties. According to the QST, the bulk LO phonons’ statistical average number can be expressed as
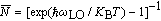 | (11) |
In the following content, numerical results for the parameters of a CsI QPD crystal system and the parameters used in our calculations are 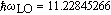
With HLI in the center of a CsI QPD, the FESE of strongly-coupled polaron as the function of the temperature has been depicted in Fig.
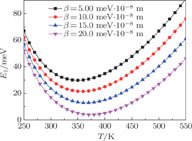 | Fig. 1. (color online) First-excited state energy E 1 versus temperature T and Coulomb impurity potential strength β. |
To observe the temperature effects and the Coulomb impurity potential strength on the polaron excitation energy in the CsI QPD, we set V
0 = 10.0 meV, R
0 = 4.0 nm, and r
0 = 12.0 nm in Fig.
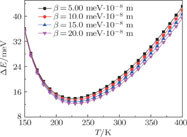 | Fig. 2. (color online) Excitation energy ΔE versus temperature T and Coulomb impurity potential strength β. |
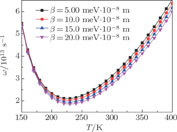 | Fig. 3. (color online) Transition frequency ω versus temperature T and Coulomb impurity potential strength β. |
As is seen from Figs.
As noted in Figs.
Here we suggest two ways to control the FESE, excitation energy and transition frequency in the CsI QPD via adjusting the temperature and adjusting the Coulomb impurity potential strength.
Moreover, the technique of controlling the temperature and Coulomb impurity potential strength may be used for building quantum information devices, which is in agreement with the results of Ji et al. [27]
The impurity and temperature effects on the FESE, excitation energy and transition frequency of bound polaron strongly-coupled with the HLI in the center of CsI QPD have been investigated. Calculations were performed by using QST and VMPT. The results were illustrated as functions of the temperature and the Coulomb impurity potential strength. It has been seen that the FESE, excitation energy and transition frequency decrease (increase) with increasing temperature in the regime of lower (higher) temperature, and they decreased with enhanced Coulomb impurity potential strength. The temperature, the pseudoharmonic and Coulomb impurity potentials are important factors for studying the polaron states’ properties in the CsI QPD with HLI located in the center of the system.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] |

