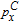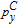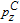† Corresponding author. E-mail:
The tight-binding Harrison model and Green’s function approach have been utilized in order to investigate the contribution of hybridized orbitals in the electronic density of states (DOS) and electronic heat capacity (EHC) for four hydrogenated structures, including monolayer chair-like, table-like, bilayer AA- and finally AB-stacked graphene. After hydrogenation, monolayer graphene and bilayer graphene are behave as semiconducting systems owning a wide direct band gap and this means that all orbitals have several states around the Fermi level. The energy gap in DOS and Schottky anomaly in EHC curves of these structures are compared together illustrating the maximum and minimum band gaps are appear for monolayer chair-like and bilayer AA-stacked graphane, respectively. In spite of these, our findings show that the maximum and minimum values of Schottky anomaly appear for hydrogenated bilayer AA-stacked and monolayer table-like configurations, respectively.
Graphene as a two-dimensional (2D) honeycomb lattice with sp2 hybridized carbon atoms discovered in 2004 and guaranteed its future applications both theoretically and experimentally.[1] Owing to its novel properties as a weird material sit is applicable in nanoelectronics and optoelectronics.[1–8] In graphene, conductance electrons are from the tangential π and π* bands at the limit of zero doping, i.e., at Dirac points of first Brillouin zone. S, px, and py orbitals are responsible for strong covalent bonding (in-plane bonding) while pz orbitals lead to the weak van der Waals bonding (out-of-plane bonding). Gapless nature of graphene limits the direct utilization of graphene in nanoelectronic and nanophotonic devices.[9,10] Thus, opening or tuning a band gap is useful for technological application of graphene, especially in highly motivated new graphene-based devices. Hydrogenation of graphene has been realized and predicted not only theoretically but also experimentally in 2007 and 2009[11,12] to induce a finite band gap. It has been found that in new 2D material, hydrogenated graphene which is called graphane with sp3 hybridization, carbon atoms react with hydrogen (H) atoms and consequently create a band gap about 3.5 eV. (In Fig.
 | Fig. 2. (color online) Schematic illustration of hydrogenated bilayer graphene and their top views for case (a) AA-stacked and (b) AB-stacked. |
Recently, several works have been done to compare the thermal properties (including thermal conductivity and temperature dependence of EHC) of low-dimensional systems with macroscale ones.[16–19] Balandin in 2011 found that graphene is the best thermal conductor in nature.[17] Furthermore, with changing in orbitals hybridization of carbon atoms, electronic properties of materials can be changed and therefore affect other properties. Hybridization from sp2 to sp3 (from graphene to graphane) leads to the changing of the dynamics of lattice charge carriers. It is necessary to mention that the thermal properties of a material have merit to find applications in thermal management and thermoelectric.[20,21] Since all nanoelectronic applications are closely related to the thermal properties, the investigation of thermodynamic properties is important. The EHC of a system defines as the ratio of the amount of heat which is used by the carriers (here, Dirac fermions) to the rising in temperature of the system. Gharekhanlou et al.[22] reported that graphane-based materials can be used as bipolar transistor and have introduced a 2D p–n junction based on graphane.[23] Savini et al.[24] used a kind of p-doped graphane to fabricate a prototype high-Tc electron–phonon superconductor.
Here, we are about to compare the partial and total DOS and EHC of these systems. We will present the corresponding results based on Green’s function calculations. Monolayer graphene with full hydrogenation and fully hydrogenated bilayer graphene are both exhibit semiconducting characteristics similarly. As long as tight-binding Harrison model describes the dynamics of charge carriers. The outline of this paper is as follows. Section
The Harrison model describes the low-energy dynamics of Dirac fermions in the honeycomb lattice for all graphene-type configurations. As shown in Fig.
 |


Other elements are HH1H1(

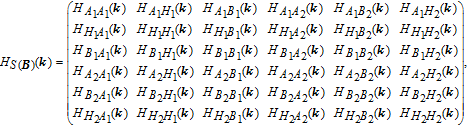




The primitive unit cell vectors of honeycomb lattice in Fig.





By substituting Eqs. (
The summation of imaginary part of Green’s function elements results the DOS.[32] By engaging Eqs. (
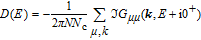
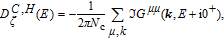
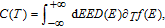
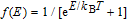
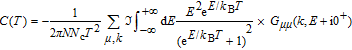

The study of C(T) in the monolayer and bilayer graphene lattice constitutes the main aim in this work. In the next section, the results are presented.
In this paper, we have obtained the total and partial electronic density of states and electronic heat capacity of monolayer and bilayer graphene in the presence of hydrogenation. We have implemented a tight-binding Harrison Hamiltonian model including local energy terms to describe the dynamics of massless Dirac and massive chiral fermions. We normalized all energies over the intra-layer hopping energy, 
 | Fig. 3. (color online) (a) The total and (b)–(f) orbital electronic densities of states for all kinds of monolayer and bilayer graphane. |
Figure
| Table 1. The total and orbital energy gaps of hydrogenated monolayer and bilayer graphene in terms of |
Figure
 | Fig. 4. (color online) (a) The total and (b)–(f) orbital electronic heat capacity for all kinds of monolayer and bilayer graphane. |
Surprisingly, the behavior of py orbitals for two monolayer and two bilayer structures are the same. As we know, each C atom has s, px, py, and pz orbitals with symmetric forms. By hydrogen doping, symmetry breaking occurs and since we have selected the x and y axes, respectively as horizontal and vertical vectors, the px orbitals from A atoms that are overlapped with that of B atoms are affected less than py orbitals because py orbitals have more accessible free space on the honeycomb lattice with this selection x–y coordinates. If we choose the y–x coordinates in our calculations, it is obvious that the px orbitals are affected more than py orbitals. For this reason, doped hydrogen does not change py orbitals interestingly and have the same contributions.
In summary, we have obtained qualitative results of electronic density of states and electronic heat capacity of the hydrogenated monolayer chair-like, table-like, bilayer AA-stacked, and AB-stacked graphene. The contribution of different orbitals on the heat capacity over a wide temperature range is compared. The Green’s function approach gives findings in Harrison model. It is concluded that the maximum and minimum band gap is for monolayer chair-like and bilayer AA-stacked graphene while the maximum and minimum Schottky anomaly is for bilayer AA-stacked graphene and monolayer table-like graphane, respectively.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] |