† Corresponding author. E-mail:
A series of material parameters are derived from atomistic simulations and implemented into a phase field (PF) model to simulate void evolution in body-centered cubic (bcc) iron subjected to different irradiation doses at different temperatures. The simulation results show good agreement with experimental observations — the porosity as a function of temperature varies in a bell-shaped manner and the void density monotonically decreases with increasing temperatures; both porosity and void density increase with increasing irradiation dose at the same temperature. Analysis reveals that the evolution of void number and size is determined by the interplay among the production, diffusion and recombination of vacancy and interstitial.
The development of fast reactor and fusion reactor requires advanced structural materials which can tolerate higher temperature and higher irradiation dose under harsh service environment.[1] Owing to their excellent irradiation swelling resistance and good fracture toughness, ferrite/martensite (FM) steel[2,3] has been developed and considered as a candidate structural material for advanced nuclear reactor applications. Body-centered cubic (bcc) iron matrix is the main component (∼90 wt%) for the complex FM steel. Irradiation effects on bcc iron, including swelling, embrittlement and other degradation of the macroscopic mechanical properties,[4–6] have attracted significant attention in the last decades. These effects are microscopically attributed to the increases in vacancy and interstitial content during continuous irradiation, resulting in voids/bubbles, dislocation loops and precipitates in the material.
Numerous efforts have been devoted to investigating the irradiation effects of the structural materials in multiscale.[7–11] As a mesoscale simulation approach, the phase field (PF) method has been widely used to study microstructure evolution in various materials. With respect to irradiation effects, the PF method can well capture the kinetic and morphological evolution of irradiation-induced voids compared with irradiation experiments. The pioneer work on simulating the effect of irradiation on void evolution was reported by Yu and Lu.[12] It was assumed that void formation is caused by spinodal instability and its growth needs continuous supplies of vacancies. In 2009, Rokkam et al. developed a PF model on the basis of Cahn–Hilliard and Allen–Cahn equations to predict the stages of void incubation, nucleation and growth under irradiation.[13] Subsequently, this model was adopted for irradiated metal to simulate void and gas bubble nucleation and annihilation in intergranular and intragranular locations.[14–21] The influence of temperature gradient on void stability and growth kinetics, which is known as the Soret effect, was virtually observed by Li et al., and the void mobility was found to strongly depend on temperature gradient rather than void size.[22] In addition, the effects of grain sizes and intergranular gas bubble sizes on the effective thermal conductivity of the irradiated polycrystalline alloy in a three-dimensional PF model were investigated, and the growth kinetics and stability of interstitial loop were found to be highly dependent on the elastic interaction between the interstitial loops and point defects.[23–28]
So far, most PF simulations of void formation and growth are based on empirical parameters[13–18,22,23] and thus are limited by the lack of real parameters of specific materials. Therefore, real material parameters, such as void/interstitial formation energy, should be taken into account with the inclusion of the temperature effect.[18] This study aims to investigate the irradiation-induced void formation and growth by considering different temperatures and irradiation doses in junction with the atomistic derived material parameters. In Section
As is well known, irradiation can generate vacancies and interstitials at the same time in the solid matrix; however, their kinetic behaviors and production during the microstructure evolution are distinctly different, that is, vacancy clusters form void and interstitial clusters form dislocation loop. Since the diffusion rate of interstitial is much faster than that of vacancy by orders of magnitude,[29] leading to the different kinetic time scales between vacancy and interstitial, the formation of dislocation loop and the effect of lattice strain relating to interstitials are not considered in the present PF model. Irradiation-induced void is a core with rich vacancies and its growth is primarily controlled by absorbing the surrounding irradiation-induced vacancies.[30]
In this work, we consider a system with two phases (i.e., matrix and void) to simulate void evolution during irradiation. Temporal and spatial variations of vacancy and interstitial concentrations in the matrix are characterized by two conserved fields, i.e., an interstitial concentration field c
i(x,t) and a vacancy concentration field c
v(x,t), where x is the spatial coordinate and t is the time. In addition, a long-range order parameter field, η(x,t), is introduced to distinguish the matrix phase (
Millett et al. [15] modified the classical Cahn–Hilliard and Allen–Cahn free energy equations for a non-uniform system by considering c i(x,t), c v(x,t), and η(x,t) to distinguish the matrix phase from the void phase. The expression of total free energy function is given by
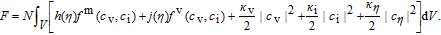 | (1) |
The free energy of the matrix phase, f m(c v,c i), includes the enthalpy and entropy terms as a function of the vacancy and interstitial concentrations in the matrix and can be written as
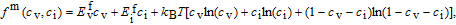 | (2) |
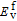
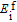
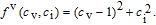 | (3) |
The gradient coefficients κ v, κ i, and κη , which depend on temperature, are related to void/matrix interfacial energy. In addition, the local free energies of the matrix and void phases are connected smoothly in the concentration-order parameter space by the following interpolation functions
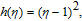 | (4) |
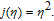 | (5) |
The time evolutions of the conserved and non-conserved fields are governed by the Cahn–Hilliard and Allen–Cahn equations, respectively, with the consideration of production (source) and recombination (sink) of the irradiation-induced point defects, that is
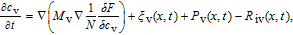 | (6) |
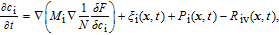 | (7) |
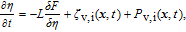 | (8) |
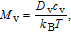 | (9) |
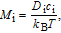 | (10) |
The Frenkel pair production rates of vacancy P
v(
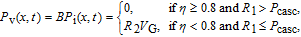 | (11) |
The units of displacements per atom (dpa) per unit time, K, namely the irradiation dose rate, can be obtained from the following equation:
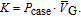 | (12) |
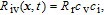 | (13) |
The above void kinetic equations are solved numerically in a two-dimensional (2D) domain with a uniform square grid and the periodic boundary condition. Three different computational cell sizes are used, i.e., 128 × 128, 256 × 256, and 512 × 512, to examine the influence of spatial resolution. It is found that the simulation results concerning void size, density and porosity are independent of system size. In this work, we present all the simulation results obtained with 256 × 256 grid points. The time step is 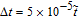
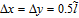
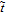

Ab initio calculations offer the possibility to qualitatively predict the thermodynamic parameters of the material used in PF simulations. Here ab initio molecular dynamics (AIMD) simulation implemented in the Vienna ab-initio simulation package (VASP),[32,33] which is based on density functional theory (DFT) and plane-wave pseudopotential technique,[34,35] is carried out to determine the formation energy of a vacancy or self-interstitial in iron solid. The interactions between ions and electrons are described by the projector-augmented wave (PAW) potential.[36,37] The electron exchange–correlation interactions are treated by the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) functional.[38,39] The plane-wave kinetic energy cutoff is chosen to be 400 eV. A 128-atom bcc supercell formed by 4 × 4 × 4 unit cells is used to model the perfect crystal of iron. The Brillouin zones are sampled by Monkhorst–Pack scheme[40] with a uniform mesh of 2 × 2 × 2
| Table 1.
Values of lattice parameter (in unit Å), cohesive energy (in unit eV), magnetic moment per atom (in unit μB), and bulk modulus (in unit GPa) for bcc iron. . |
The MD time step is 1.0 fs and the total simulation time is 15 ps. The AIMD simulations within the canonical ensembles (NVT) use the Nosé–Hoover thermostat to control the temperatures at 293 K, 513 K, 622 K, 722 K, and 822 K, respectively. The temperature-dependent lattice parameters of bcc iron are taken from the experimental data.[45,46] At a given temperature, the formation energy of a vacancy or interstitial is obtained by averaging the free energy of each step of the last 10-ps AIMD simulation after the first 5-ps equilibration. At temperatures of 293 K, 513 K, 623 K, 722 K, and 822 K, the vacancy formation energies are 2.058 eV, 2.162 eV, 2.243 eV, 2.242 eV, and 2.288 eV, respectively, and the interstitial formation energies are 3.384 eV, 3.277 eV, 3.145 eV, 3.035 eV, and 3.002 eV, respectively. According to our DFT calculations, producing an interstitial in the perfect crystal of iron requires more energy than producing a vacancy. More interestingly, the formation energies of vacancy and interstitial show opposite trends of temperature dependence, i.e., 
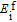
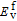
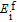

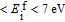
Diffusivities of vacancy (D v) and interstitial (D i) in iron host are related to temperature via the Arrhenius diffusion equation
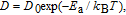 | (14) |
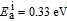
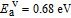
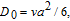 | (15) |
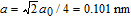
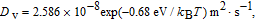 | (16) |
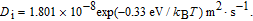 | (17) |
The gradient coefficient κ is used to describe the interface between void and matrix. κ v, κ i, and κη used in this model are assumed to be the same. In general, κ is related to the interfacial energy γ as
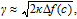 | (18) |
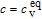
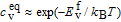
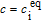
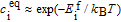
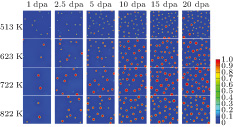
As demonstrated in previous studies,[14–18] PF model is able to capture void formation and growth in material during irradiation, exhibiting many interesting phenomena on a mesoscale. One significant aspect is the formation of irradiation-induced void, leading to the changes of the material properties. The vacancies and interstitials produced in the form of Frenkel pairs are randomly distributed in bcc iron. The on-going production of vacancies leads to vacancy accumulation, which finally gives rise to void formation.
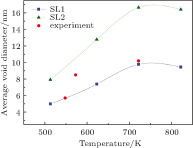
The temperature-dependent mean void diameters of 1 dpa irradiated iron are given in
To further elucidate the role of temperature-dependent parameters used in the PF simulations, the values for bcc iron parameters (e.g., E
f, D, and κ) relying on temperature are now assumed to be temperature independent and are the same as those of 293 K (referred to as SL2). As seen in
As for 2D simulation, instead of swelling, porosity defined as the fraction of all voids over the total volume can be used to characterize the irradiation effect.[15,16,18,21]
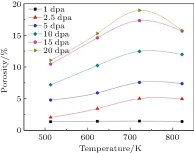 | Fig. 3. (color online) Plots of porosity versus temperature at different irradiation doses of the saturated voids in the irradiated iron. |
The plots of void density versus temperature at different irradiation doses are shown in
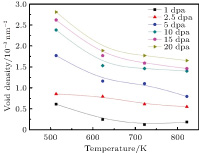 | Fig. 4. (color online) Plots of void density versus temperature at different irradiation doses of the saturated voids in the irradiated iron. |
It should be mentioned that the present 2D PF model is insufficient to give a complete description of the initial nucleation of void as well as the continuous growth process that is influenced by dislocation and lattice strain. Nevertheless, it does capture the essential features of void evolution (e.g., void size and density) affected by temperature and irradiation dose. In addition, there is a wide space to extend the current irradiation-induced void PF model for other candidate nuclear materials used in fast reactors and fusion reactors, such as vanadium alloys and SiC, aiming to gain an important understanding of void evolution in the irradiated materials. In future study, the consideration of void nucleation should be improved by introducing the explicit nucleation algorithm[30] and would include the effect of dislocation on the void evolution by using the results from molecular dynamics (MD) or other simulation methods.
With the real material parameters derived from atomistic calculations, the PF model is used to study the kinetics of void formation and growth in a single crystal of bcc iron under irradiation. Ab initio molecular dynamics simulations are performed to obtain the temperature-dependent formation energies of vacancy and interstitial. Other key parameters (e.g., vacancy/interstitial diffusivity) used in the PF model are calculated with data from atomistic simulations through using empirical formula.
Void evolution influenced by temperature and irradiation dose is predicted and analyzed. The predicted void size of the irradiated bcc iron increases with increasing temperature and then shows a slow decrease. This evolution tendency is in accordance with the experimentally measured void size. In addition, the void sizes predicted by the temperature-independent parameters in conjunction with the PF model show an obvious deviation from the temperature-dependent cases and the experimental data. Hence, it is necessary to consider the temperature effect on the material properties (E f, D, and κ) to simulate the irradiation-induced voids in a real material. With increasing temperature, the simulated porosity exhibits a bell-shaped trend and the monotonical decrease of void density, which are observed in the irradiation experiments of ferrite steels. A higher irradiation dose induces more void formation, leading to an increase in porosity and void density. In conclusion, the current PF model with realistic material parameters incorporated is able to describe the void formation and evolution in bcc iron or ferrite steels under irradiation.
Based on the feasibility demonstrated with the present phase-field approach with atomistic derived parameters, our future work will focus on the development of the descriptions of the kinetic behaviors of vacancy and interstitial (e.g., to form dislocation and to induce lattice strain) within the PF framework to more accurately capture the irradiation-induced void evolution in the bcc materials.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] | |
| [35] | |
| [36] | |
| [37] | |
| [38] | |
| [39] | |
| [40] | |
| [41] | |
| [42] | |
| [43] | |
| [44] | |
| [45] | |
| [46] | |
| [47] | |
| [48] | |
| [49] | |
| [50] | |
| [51] | |
| [52] | |
| [53] | |
| [54] | |
| [55] | |
| [56] | |
| [57] | |
| [58] | |
| [59] |