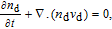Lower order three-dimensional Burgers equation having non-Maxwellian ions in dusty plasmas
Center for Applied Mathematics, Siksha ‘O’ Anusandhan University, Khandagiri, Bhubaneswar-751030, Odisha, India
† Corresponding author. E-mail:
apulnarayan@gmail.com
1. IntroductionEver since the modifications of the existing plasma wave spectra of low frequency dust acoustic waves (DAWs) involving mobile dust grains, numerous work has been done in different aspects of dusty plasma waves.[1–22] Basically, most of the investigations focus on the studies of the plasma characteristics by probing the evolutions of shock or solitary wave profile governed by the family of Burgers, K-dV and Sagdeev potential-type equations. On the other hand, it has been reported that the presence of fast ions and electrons which exist inevitably in space and laboratory plasma environments clearly specify the reason why the charged species deviate from the classical Maxwellian velocity distributions due to such particles being trapped. In fact, due to the existence of such deviations, the fascinating natures of solitons and shocks come into effect which are not pragmatic with isothermal species. It has been reported veritably that the presence of non-isothermal electrons in plasma gives rise to many interesting characteristics in the nonlinear propagations of waves, including the excitations of ions-acoustic solitary waves.[23–25] Thus the exploration of nonlinear behavior of non-isothermal plasmas having unmagnetized as well as magnetized background[26–29] has received considerable attention and has been studied by a number of authors in the last few years.
It has been found that there is a significant decrease (increase) in the amplitude (width) of the solitary wave with increasing non-Maxwellian ion population species.[24] Very recently Adhikary et al.[28] reported the dependence of solitary wave’s amplitude and width on non-Maxwellian ion concentrations and trapping of electrons. Dev et al.[29] reported the formations of spiky solitary waves in cold, dusty plasma in the presence of non-Maxwellian electrons and vortex-like electrons distributions. El-Shewy et al. studied spatiotemporal fractional KdV–Burgers equation for dust acoustic shock wave in dusty plasma with non-thermal ions by using the fractional sub-equations method.[30] Shahmansouri studied suprathermality effect on propagation properties of ion acoustic waves and concluded that in the presence of ion and electron suprathermality, the solitary wave of either polarity is possible.[31] Rehman studied electrostatic dust acoustic solitons in pair-ion-electron plasmas and came to the conclusions that electrostatic hump (dip) structures can be found when the dust particles are positively (negatively).[32] Apart from non-magnetized plasmas, little work has also been done on magnetized plasmas with non-Maxwellian ions and non-isothermal electrons. For example, recently Abrishami and Kadijani[33] reported that such a plasma is found to support two types of nonlinear solitary structures (fast and slow) which attain a higher velocity (or amplitude) when the numbers of dust grains and trapped electrons are increased. On the other hand, apart from negatively charged dust grains in the presence of magnetic field,[34–36] few observations on the features of solitary wave in the presence of positively charged dust grains in magnetized plasma has carried out. For example, Haider et al. observed spiky solitary wave in the presence of positive ions, positive dust in the presence of external magnetic field in multicomponent dusty plasma.[37] El-Wakil et al. observed that temperature, obliqueness of propagations as well as cyclotron frequencies have an imperative role in controlling the behavior of solitary wave in magnetized plasma with opposite polarity of dust.[38] Zobaer et al. derived K–dV and Burgers equations to study DA waves in strongly coupled dusty plasma in the presence of arbitrary (negative and positive) charged dust grains and observed that due to the presence of both type of charges, such a plasma system causes the presence of opposite potential (positive and negative) DA solitons and shock structures and significantly modifies its basic features.[39]
Shock waves in dusty plasma with non-Maxwellian ion distribution and charge fluctuating negative dust have been studied in diverse ways and the emphasis is mainly placed on the modifications of basic properties of shock, such as amplitude, propagations speed, etc. due to the presence of such species.[40,41] Recently Tasnim et al.[42] discussed the effect of dust kinematic viscosity in non-Maxwellian dusty plasma with two population ions and found a significant modification in the basic properties such as amplitudes, width, and polarities of the DA shock wave (DASHW). They reported the smoothness and the weakness of the shock profile due to dissipative force which arises because of dust charge fluctuations in non-Maxwellian ion plasma environment. Their investigations also well indicated that the magnitude of the amplitude of positive (negative) shock wave increases (decreases) with the increase of temperature ratio of non-Maxwellian ions. Furthermore, they concluded that the amplitudes (widths) of positive and negative shock waves increase (decrease) with the increase of phase velocity. Asaduzzaman and Mamun[43] studied the modifications of dispersion properties of the DAWS due to the presence of nonthermal ions and polarizations force. It has also been found that the phase speed of the DAW, increases with the increase of non-Maxwellian ion. Kannou and Annou[44] in their report discussed the importance of non-Maxwellian ions for the occurrence of solitons and indicated that the only rarefactive soliton is possible. However Pakazad[45] interestingly defined the range of non-Maxwellian ion concentrations for the existence of both compressive and rarefactive solitons in warm dusty plasma in the presence of non-Maxwellian ions. On the other hand, in many observations it has been reported that transverse perturbations always exist in a higher-dimensional system; especially at higher polar altitude or even in laboratory case. So, a purely one-dimensional model can account for none of all observed features since the wave structure and many properties of the solitary waves are modified by these transverse perturbations.[46,47] Motivated by these observations, Zobaer et al.[48] and Mamun and Zobaer[49] derived first a modified Burgers equations in the planar case with adiabatic pressure; however, very few investigations have been done on the derivations of a two-dimensional Burgers equations.[50] Furthermore to the best of our knowledge, no observation has been reported on three-dimensional (3D) Burgers equations except a few observations by this author.[51,52]
In this model, we study the establishment of DA shock waves in a dusty plasma with two-temperature (high and low temperature) non-Maxwellian ions and non-isothermal electrons by deriving the lower order modified 3D Burgers equation through using reductive perturbation techniques. To the best of our knowledge, no analysis has been reported where the effects of the populations of high and low non-Maxwellian and non-isothermal electrons on the shock wave characteristic are studied by using the lower order modified 3D Burgers equations.
2. Basic equations and formulations of the problemThe continuity and momentum equations for the dusty plasma are as follows:
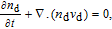 | (1) |
 | (2) |
Together with the charge neutrality equations  where ne0, nd0, nih0 (nil0) are the unperturbed number of electrons density, dust density, and higher (lower) density ions respectively. Zd0 is the equilibrium dust charge. Then, the following Poisson’s equation is obtained:
where ne0, nd0, nih0 (nil0) are the unperturbed number of electrons density, dust density, and higher (lower) density ions respectively. Zd0 is the equilibrium dust charge. Then, the following Poisson’s equation is obtained:
 | (3) |
where
φ,
Zd,
md, and
vd are the electrostatic potential, dust charge numbers, mass of the dust particle, and the dust fluid speed. Now considering DA wave propagations in collisions-less unmagnetized dusty plasma with non-isothermal electrons, and low and high temperature non-Maxwellian ions, their densities are given respectively by
 | (7) |
where
ε is a small dimensionless parameter measuring the weakness of the dispersions and and
V0 is the nonlinear wave velocity. The dynamical variables are expanded as power series of
ε as follows:
 | (8) |
Substituting Eqs. (7) and (8) into Eqs. (6a)–(6d), and equating the coefficients of the lowest order in ε, we obtain
 | (11) |
where

,

,
R2 =
p2/
μ′,
C = 5
γ1σ + 3/6
V0γ1.
Now the stationary solution of lower order modified 3D Burgers equation is as follows:
 | (12) |
where
ϕm = 3/4{
Ul −
C(1 −
l2)}/
Al2 and
w = 4
Bl3/{
Ul −
C(1 −
l2)} are the amplitude and width of the shock wave respectively, with
l being the direction cosine and
U being the velocity.
4. Results and discussionThe effects of various dusty plasma parameters on the propagation of electrostatic shock wave are examined numerically from the lower order modified 3D Burgers equation. The dust particles in the plasma are considered to be uniform in size with fluctuating negative charge while the plasma ions is assumed to be singly charged two-temperature non-Maxwellian ions and non-isothermal electrons.
Figure 1 depicts the variations of the nonlinear co-efficient A with non-isothermal electron temperature υ for different populations of high and low non-Maxwellian ions. Here the other plasma parameters are considered to be ne0 = 3 × 1014 m−3, ni0 = 5 × 1014 m−3, nd0 = 1010 m−3, zd0 = 2 × 104e, Ti = 0.16 eV, and Td = 0.06 eV.[4,51] It is seen that with increasing v, i.e., the ratio of effective electron temperature to non-isothermal electron temperature, the nonlinear coefficient decreases and approaches to zero as the ratio becomes one. This is because the system approaches to thermal equilibrium, the nonlinearity obviously decreases. In addition, a dominant role of density of high temperature non thermal ions in the variation of A is also seen. As seen from the figure, as we move from the lower solid (blue) plot to the upper solid (orange) plot, the density of high temperature non thermal ions increases significantly. And as it is evident that the increase in density will always result in the decrease of phase velocity due to increased rate of collision. This rate of increase in collision and hence the decrease in phase velocity will be greater in the case of high temperature non Maxwellian ions, as the high temperature non Maxwellian ions are more prone to suffering a collision frequently due to their increased number density. Thus the rate of decrease in phase velocity and hence the rate of increase in A will be greater for the case involving more high temperature non thermal ion which is the condition for the upper solid (orange) plot than for the other two plots. Interestingly if we compare the lower solid (blue) plot with the middle dash plot, it is clear that though we reduce the number density of low temperature nonthermal ions and increase the density of high temperature non thermal ions, the value of A increases and thus we may see a dominant role of high temperature non thermal ion species in the process.
Figure 2 indicates that the nonlinear coefficient A increases with increasing population of non-Maxwellian ions and interestingly the range of α for the same enhancement of A is different for the different population density of non-Maxwellian ions. For example, the range of α for the most left solid (orange) curve is between 0 and 0.6 while for the most right solid (blue) curve the range is between 0 and 0.9. The reason for this phenomenon is that in the most left curve, the number of high temperature non-Maxwellian ions is more than the number of low temperature non-Maxwellian ions, and this should eventually increase the phase velocity since velocity is a manifestation of temperature. But on the other hand, since we are interested in the non-Maxwellian ion populations, which will definitely reduce the phase velocity because with increasing the number density, the charged particle will suffer more collisions. This rate of decrease in phase velocity will be higher in the case of high temperature non-Maxwellian ions than in the case of low temperature non-Maxwellian ions as the high temperature non-Maxwellian ions are more prone to suffering collision frequently than low temperature non-Maxwellian ions due to their increased thermal velocity. And since nonlinear coefficient A is an inverse function of phase velocity, so the rate of enhancement in A will be higher for the case involving more high temperature non-Maxwellian ions (the most left solid curve of Fig. 2) than less high temperature non-Maxwellian ions (extreme right solid curve of Fig. 2).
Figures 3 and 4 show clearly the physical situations involved in the processes in terms of thermal velocity of the plasma species. In both the figures, the densities of both the ions are the same and the temperature of high temperature non-thermal ions is varying. Now if we compare both the figures, the dominant physical parameter involved in the process is the temperature of high temperature non-thermal ions (Fig. 4), with other variables kept fixed for both figures. Now it is evident that the increase of temperature results in an increase of the thermal velocity of the plasma species, and as a result the phase velocity increases which results in a reduction in the value of A in Fig. 4 compared with in Fig. 3 where the temperature of high temperature non-thermal ions is less than the value considered for Fig. 4.
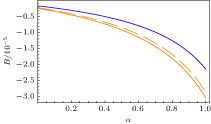
The characteristics of dissipative coefficient B as a functions of α for the different density ratios are plotted in Fig. 5, and it is clear that the dissipative coefficient increases with increasing non-Maxwellian ion population density. This may be because for the present plasma system under consideration, we have assumed that dust charge fluctuations is the source of dissipations and that the dissipative coefficient B is an inverse functions of normalized decay rate, the increase (decrease) of decay rate will reduce (increase) the value of B. Now, this can be attributed to the fact that with increasing non-Maxwellian ion population, there will be an enhancement in the dust charge quantity which conduces to the increase of dust plasma frequency, thereby reducing the decay rate which results in the increase of B. On the other hand, looking into the second aspect of the figure, we can see that the ranges of α are different for almost the same rate of increase of B for different high and low temperature non-Maxwellian ions. Now if we examine the physical situations of all the three curves, we see that in the case of the most left solid curve, the value of high temperature non-Maxwellian ions is significantly higher than that of the low temperature non-Maxwellian ions, which keeps decreasing further as we move it towards the most right solid curve. Now, we know that the dust charge increases significantly with the ion (or electron ) thermal velocity, so corresponding increase in dust charge and hence an increase in the dust plasma frequency will be observed for the most left solid curve. This will result in a rapid decrease in the decay rate, which will conduce to a vast increase in the value of B compared with the other two curves in the figure, since for the other two curves the dust charge and hence the dust plasma frequency will keep decreasing because of the decrease in temperature of the non-Maxwellian ions.
Figure 6 describes the spatial variations of shock potential profile for different ranges of low and high temperature ions with different ranges of temperature in the absence of non-Maxwellian ions and non-isothermal electrons. Here the other plasma parameters are kept similar to those in Fig. 1. Now if we examine the physical situations in the lower solid and middle dash curves, it is apparent that in the lower solid curve, the increased density of the high temperature Maxwellian ions will result in an increased collisions of the plasma species compared with in the middle dash curve. This increased collisions will result in a decrease in the phase velocity which in turn increases the value of nonlinear coefficient A. Now this enhancement in the nonlinear coefficient A further reduces the shock potential which is the case for the lower solid curve. Similarly for the upper solid curve, significant reduction in the temperature of especially high temperature ion species results in the increase of phase velocity due to fewer collisions than that in the physical situations of other two curves discussed above. This in turn reduces the value of the nonlinear coefficient A and hence increases the shock potential considerably.
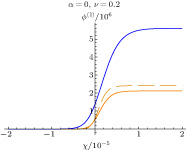
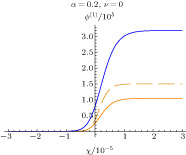
On the other hand, figures 7 and 8 show the spatial evolutions of shock potential profile for Maxwellian ions and non-Maxwellian ions in the presence of non-isothermal electrons and flat trapped electrons, respectively. The shock wave potentials for all the three curves of both the figures are higher in the presence of trapped electrons than in the absence of trapped electrons. This is obvious because in the presence of trapped electrons, the nonlinearity decreases, which eventually increases the height of the shock potential profile. So, that is why the shock potential profile shows significant increase in the presence of trapped electrons. On the other hand, the individual variation of the shock potential profile of each of Figs. 7 and 8 can be understood in the context of the explanations of Fig. 6 as the other physical parameters are invariant in all the three curves. In Fig. 9 the simultaneous effects of non-Maxwellian ions and trapped electrons are presented to have clear comparisons among the shock potential profiles of the other three figures, i.e., Figs. 6–8. Here also the individual variations of the shock potential profile can be understood in a similar way to that discussed above in Figs. 6–8. Now, the most interesting fact is that if we compare Fig. 7 with Fig. 8, it can be concluded that for the present plasma model under consideration, shock wave has maximum amplitude in a Maxwellian ion plasma in the presence of trapped electrons (Fig. 7) and minimum amplitude with non-Maxwellian ion plasma in the presence of flat trapped distribution of electrons (Fig. 8). On the other hand, as depicted in Fig. 9, it is seen that due to the possible simultaneous interplay between non-Maxwellianity and trapping in the plasma, the value of the shock potential becomes lower significantly than the shock potential value with Maxwellian-flat trapped distribution of plasma species (Fig. 6).
5. ConclusionsA specific theoretical analysis of DA waves in an unmagnetized dusty plasma system containing non-Maxwellian ions and non-isothermal electrons is investigated by deriving the lower order modified 3D Burgers equation with dust charge fluctuations. It is perceived that the ion temperature ratio, non-Maxwellian ions and non-isothermal electrons have a momentous effect on forming different forms of positive shock wave structures. Equation (9b) clearly depicts that the phase velocity V0 directly depends on the dust for effective temperature ratio. We find that the population of low and heigh temperperature non-Maxwellian ions α and non-isothermal electron temperature ratio ν give the polarity of the shock-like structure in our model. Also the shock potential reaches maximum (minimum) value with Maxwellian-trapped (non Maxwellian-flat trapped) plasma species. This result might be useful for different types of space plasmas and astrophysical plasmas and also for the experimental research of observing the shock structure in negative dust charge fluctuations in the presence of non-Maxwellian ions and non-isohermal electrons distributions.[53–57]