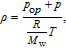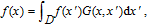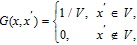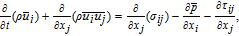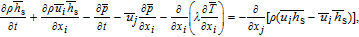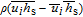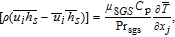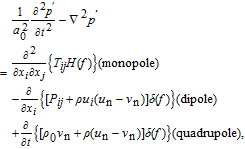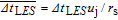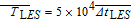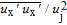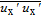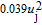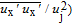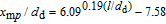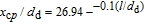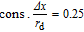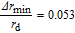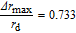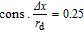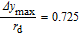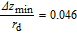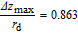Numerical investigation of the interaction of the turbulent dual-jet and acoustic propagation
School of Metallurgy, Northeastern University, Shenyang 110819, China
† Corresponding author. E-mail:
libk@smm.neu.edu.cn
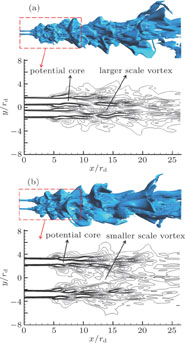
1. IntroductionThe turbulent jet has been extensively used in various applications such as spraying, heating, and cooling processes. The noise emissions from dual or multiple jets pose a serious problem in many engineering devices, including the boiler combustion chamber, ejectors in the heavy-lift rockets, V/STOL aircrafts, air film cooling, fuel injection systems, heating, and air-conditioning systems, etc. The single jet flow can be categorized into three regions as shown in Fig. 1(a): mixed region, transition region, and full-developed region. A small high-speed stream is observed at the nozzle exit. The influence region reduces rapidly once it leaves the exit, and this region is named the potential core. A large gradient can be found around the potential core due to the vigorous entrainment of surrounding fluid. It is expected to be the uppermost acoustic source of noise emission. The flow pattern of dual-jet is more complicated as displayed in Fig. 1(b). Due to the interaction between the two jets, a sub-atmospheric region is created near the nozzle exit (i.e., the converging region), resulting in a deflection of each jet. The two inner shear layers merge together at the merging point (MP). At the downstream of the merging region, the jet centerlines continue to attract together until reaching the combined point (CP). After this point, in the combined region, the two jets eventually combine, resembling a single jet performance further downstream. Because of the mutual attraction and the merging phenomenon of the dual-jet, the noise generation and its associated spatial propagation could exhibit some distinguished features compared with the single jet.
It is supposed to precisely measure flow properties and aerodynamic noises in the experiments.[1–8] With the rapid development of computation resources, numerical simulation has been adopted to solve the acoustic problem. Considering the computation load and time, although the direct numerical simulation (DNS) has a higher accuracy, large-eddy simulation (LES) is invoked in the present work. The LES numerical investigation of the turbulent jet was presented by Zhang et al.
[9] to study the instantaneous and statistical velocity fields. Bogey and Bailly[10] also used the LES to predict jet noise emission and proposed a set of spectra and azimuthal correlation functions for the acoustic radiation. On the other hand, a simplification of computational aeroacoustics for engineering applications is also essential. The widely used Lighthill acoustic analogy is an exact rearrangement of the continuity and the Navier–Stokes equations, and several derivatives of this formulation have been applied to noise emissions. For example, the acoustic perturbation equation (APE) has been proved to be an amenable numerical approach, containing convection and refraction effects in noise propagation. Nevertheless, several authors discovered that the convection and refraction effects just play an insignificant part of the Lighthill sources because only a small portion of them can radiate to the far field and considerable cancellations take place among the acoustic sources.[11–15] Driven by its wide adoption by researchers, the integral surface methods of the FW-H model and the Kirchhoff model have been compared with each other by Rahier et al.
[16] in the acoustic simulation of thermal jet. They concluded that the Kirchhoff model based on density algorithm may give an incorrect noise prediction. Based on the above reason, the LES/FW-H coupling method is adopted in the present work for turbulent jet noise prediction.
A literature review shows that most of the previous studies concerned the single jet noise prediction. Only a very little work focused on the flow structure and the noise prediction of the dual-jet. One of the earliest attempts was made by Miller and Comings.[17] They compared a dual-jet flow structure with a single free jet structure. Tanaka[18,19] reported the flow characteristics of a dual-jet in the merging and the combined regions, using an experimental approach. Okamoto et al.
[20] measured the mean velocity field of a parallel dual circular jet at two different separation distances. The effects of ambient pressure ratio and jet spacing on the high-speed dual-jet were investigated by Moustafa.[21] Faghani and Rogak[22] developed a semi-analytical model to predict the velocity field of the dual circular jets. Anderson et al.
[23] conducted an experiment to study the periodic vortex shedding phenomenon in a dual-jet flow, where the effect of separation distance on the vortex shedding was further investigated by Mondal et al.
[24] Greco et al.[25] experimentally investigated the impinging single and dual circular jets to compare the time-averaged behavior of velocity components. In regard to the noise prediction, Kanyola[26] performed experiments on a heated dual-jet to evaluate the effects of turbulent mixing and acoustic shielding on jet noise by varying the separation distances. He found that the noise generated from the dual-jet was lower than the sum of acoustic energy from two independent jets. Raman and Taghavi[27] described the influence of jet separation distance on the complex interaction in greater detail. Viswanathan[28,29] reported on a database of dual-jet noise under different parameters such as Mach number and nozzle area ratio.
As mentioned above, the work dealing with the flow field and the acoustic properties of the dual-jet at a relatively high Mach number and a low Reynolds number is very limited. However, there is a pressing need to explore the complicated merging phenomenon between two jets. In the present work, we attempt to fill this gap by developing a complex mathematical simulation. The aim is to study the complicated interaction of a dual-jet, which exhibits some distinguishing features different from the single jet. The LES/FW-H coupling model has been used to investigate the flow structure and the acoustic propagation. In the first part, flow parameters, mathematical model and computational method are introduced. In the second part, the single-stream jet at Mach number 0.9 and Reynolds number 3600 is investigated, and flow characteristic and noise generation mechanism are analyzed. The mean flow and the acoustical field show good agreement with experimental data by Stromberg et al.[30] and numerical results by Freund,[31] which are both under the same parameters and geometries. In the third part, based on the area equivalent principle,[32,33] two parallel-flow jets are examined so as to demonstrate the phenomenological behavior of the dual-jet and its influences on flow field and noise characteristics.
2. Model development2.1. Mathematical model2.1.1. Fluid dynamics modelThe aerodynamic noise of the turbulent jet is produced by disorganized and changeable vortexes in a wide range of length and timescales, which continuously generate, evolve and decline over time. In order to obtain a reliable accuracy, various vortexes on different scales in the flow need to be captured, and detailed turbulent flow structures (e.g. turbulent fluctuations and Lighthill stresses) need to be solved for acoustic modeling. LES is such an efficient approach that can solve large-scale eddies directly and filter small-scale eddies by using a sub-grid scale (SGS) model.
In a high-speed flow turbulent jet, the compressibility must be taken into account. The fluid behaves like an ideal gas, therefore, the ideal-gas assumption is used in the present work. For a compressible flow, the ideal gas law is written in the following form:
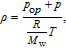 | (1) |
where
ρ is the flow density,
p
op is the operating pressure,
p is the local static pressure relative to operating pressure,
R
is the universal gas constant, and
M
w is the molecular weight. The temperature
T will be computed from the energy equation.
The governing equations employed for LES are obtained by filtering the time-dependent Navier–Stokes equations in either Fourier (wave-number) space or configuration (physical) space. A filtered variable is defined as
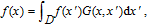 | (2) |
where
D is the fluid domain, and
G is the filter function that determines the scale of resolved eddies. The filter function
G(
x,
x') implied here is
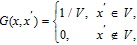 | (3) |
where
V is the volume of a computational cell (i.e., the mesh spacing).
The filtered continuity and the momentum equations are expressed as follows:
 | (4) |
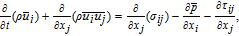 | (5) |
where
σ
ij
is the stress tensor and
τ
ij
is the sub-grid scale stress.
Filtering the energy equation, one obtains
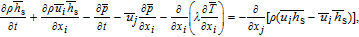 | (6) |
where
h
s and
λ are the sensible enthalpy and the thermal conductivity, respectively.
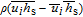
is the sub-grid enthalpy flux term approximated by using the gradient hypothesis:
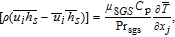 | (7) |
where
C
p is the specific heat,
μ
SGS is the sub-grid viscosity, and Pr
SGS is the sub-grid Prandtl number equal to 0.85.
2.1.2. Acoustic modelIn the present work, the problem of jet noise can be assumed to be free-space flow without obstacles between sound sources and receivers. The development of aerodynamic acoustics originates from the Lighthill acoustic analogy equation, which is a rearrangement of the equations describing the conservation of mass and momentum.[34,35] Deriving the sound source term from N-S equation, the Lighthill equation gives
 | (8) |
where
a
0 is the sound speed in the fluid medium,
Q is the mass source in the continuity equation,
F
is the body force, and
T
ij
is the Lighthill stress tensor.
The FW-H equation is essentially an inhomogeneous wave equation that can be written as
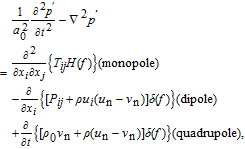 | (9) |
where surface
f = 0 is the acoustic source (emission) surface,
u
i
is the fluid velocity component in the
x
i
direction,
u
n
is the fluid velocity component normal to the acoustic surface,
v
n
is the surface velocity component normal to the acoustic surface,
H(
f) is the Heaviside function,
δ(
f) is the Dirac delta function,
p′ is the sound pressure at far field (
p′ =
p −
p0), and
Pij is the compressive stress tensor.
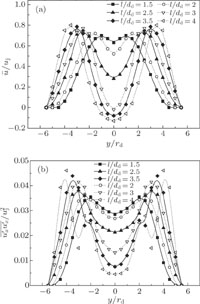
Monopole acoustic source corresponds to one source, caused by unsteady mass injection. Dipole acoustic source corresponds to two monopole sources, caused by unsteady external forces. Quadrupole acoustic source corresponds to two dipole sources, caused by unsteady shear stresses.
2.2. Geometrical description and flow parametersThe subjects of the present work are a single-stream circular jet and an equivalent parallel dual-jet that exhausts into the quiescent medium, known as free jet. The high-speed turbulent jets are at Mach number 0.9. The Reynolds number R
e = ρjujdj/µj = 3600, where the subscript j denotes the nozzle exit condition. The quantities ρj, uj, dj, µj represent the density, velocity, diameter, and viscosity of the jet at the nozzle exit, respectively. The jet has a constant stagnation temperature T
j/T
∞ = 0.86, where T
j is the jet temperature at nozzle exit and T
∞ is the temperature in ambient fluid. A pressure boundary condition is used at the outlet and radial far-field where the gauge pressure is set to be zero, with the local atmospheric pressure fixed at 101325 Pa. These parameters of the single jet match with those in the previous experimental study performed by Stromberg et al.[30] and DNS numerical simulation conducted by Freund.[31] Based on the area equivalent principle, the dual-jet is designed for constant area equivalent to that of the single jet, under the same flow parameters and computational configuration.
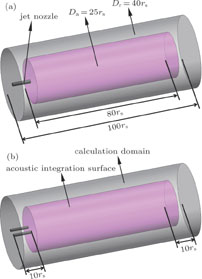
The aperture ratio is the key parameter affecting the dual-jet merging which is defined as l/d
d, where the d
d represents the injection orifice diameter and l is the jet spacing between two nozzles. There are six different aperture ratios ranging from 1.5 to 4 in the present investigation. Figure 2 displays sketches of the three-dimensional geometrical arrangement of the single jet and the dual-jet. The free jet region in which the flow equation and the acoustic integration can be solved is specified by a physical domain of 100r
s in the axial streamwise direction and 40r
s in the radial direction, where r
s is the single jet radius of the nozzle exit. One can notice that such a computational domain is sufficiently large to imitate the anechoic boundary conditions. Furthermore, the inlet tube of 10r
s in length is also specified to avoid the influence of inflow conditions. Based on the previous work, the most dominant sound source is in the potential core. The acoustic integration surfaces in the two models are sufficiently large to cover the majority of sound sources.
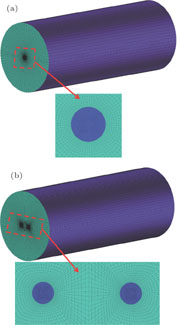
The LES model is based on the approach to resolving large turbulent structures in space which requires a substantially fine grid and considerably small time step. The model also makes use of the grid for filtering out the sub-grid scale turbulence. The single jet grid and the dual-jet grid of l/d
d = 4 are shown in Fig. 3. The computational grids are assigned by the hexahedron elements with small length scales to improve the precision of stream turbulence. For avoiding a singularity on the axis of cylindrical coordinate, O-block mesh division is used in the inlet tube section, resulting in a total number of 1200 nodes in the single nozzle exit. In the free region of the single jet, the compressible flow equations are additionally discretized with 400×40×80 grid points in the axial, radial and azimuthal directions respectively. Further details of the grid parameters are given in Table 1.
Table 1.
Table 1.
 | Table 1.
Grid specifications for single jet and dual-jet.
. |
2.3. Simulation details and boundary conditionsThe integral method based on acoustic analogy consists of two major steps. Firstly, the time histories of the relevant variables (e.g. pressure, velocity, and density) on the selected source surfaces are obtained from the time-accurate flow solution. Secondly, the sound pressure signals at the specified receiver locations are evaluated based on the collected source data by solving the generation and propagation of acoustic waves analytically.
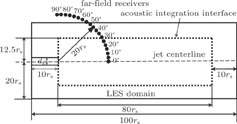
The FW-H formulation based on the most general form of Lighthill’s acoustic analogy is capable of predicting sound generation and propagation by equivalent acoustic sources. The advantage of this algorithm is far-field noise prediction, even the receiver locations fall outside of the computational domain. Figure 4 illustrates the locations of the specified acoustic receivers. Considering the noise attenuation in space as well as the aerodynamic fluctuations in computational domain, the distances between acoustic receivers and jet nozzle exit are defined as 20r
s, 40r
s, and 60r
s. There are 19 receivers (each with 5
°
from 0
°
to 90
°
) in a specified arc to record the acoustic data in different directions.
Considering the compressibility of high-speed flow, density-based formulation is adopted to solve the coupled governing equations of continuity, momentum and energy simultaneously. Each equation in the coupled system is linearized explicitly, and the solution is updated by using a multi-stage (Runge–Kutta) solver. The LES approach is used to simulate the jet flow field and the SGS model is adopted to solve the sub-grid turbulence effects (i.e., small eddies, swirls and vortices). The viscosity is approximated by Sutherland kinetic theory. For LES explicit-time formulation, the standard Roe flux difference splitting (Roe-FDS) scheme is used in the spatial discretization. The time step size of fluid dynamics model is set to be Δt
LES = 0.8rs/a0. The sampling rate is defined as
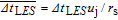 and the total sampling time is
and the total sampling time is
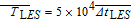 . After the fluid field has become steady and well-developed state, the acoustic modeling is then to simulate acoustic field and noise propagation for a period of
. After the fluid field has become steady and well-developed state, the acoustic modeling is then to simulate acoustic field and noise propagation for a period of
where Δ
t
FWH and
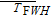
indicate the sampling rate and the total sampling time in the acoustic calculations, respectively. This period is far longer than the time interval an acoustic wave can propagate through the computational domain. The highest frequency of sound field in acoustic calculation (fast Fourier transform) is inversely proportional to the time step as expressed by
f
max = 1/2
t
FWH. The sound frequency range that a human ear can hear is from 20 Hz to 20 kHz, thereby the time step size of the acoustic model is specified as Δ
t
FWH = 2.5 × 10
−5.
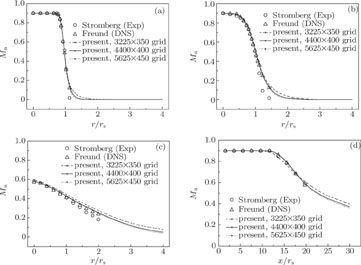
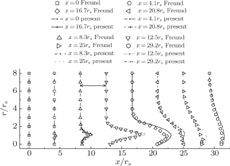
3. Results and discussion3.1. Single jet model3.1.1. Flow structure and model validationThe time-averaged Mach numbers from the transient flow data are depicted in Fig. 5. The results are validated against the experimental data by Stromberg et al.[30] and the DNS results by Freund.[31] To verify that the predicted results are grid independent, a grid sensitivity study is carried out from the Mach number distributions as shown in Fig. 5. In general, the differences are found to be minor for grid refinement. The solutions for the medium mesh (i.e., 4400×400 grid) pose considerable differences from those for the coarse mesh (i.e., 3225×350 grid). Nevertheless, the differences between the medium mesh and the fine mesh (i.e., 5625×450 grid) are negligible. Hence, the medium mesh (i.e., 4400×400 grid) is used for all the single jet cases studied. The results show that they are in reasonable agreement with both experimental and numerical results. The main disagreement with the experimental data in the downstream may be due to the measuring method. In the downstream, the mean flow is too weak to measure the accurate velocity profile by using the Pitot probe. An essential feature of the turbulent free jet is the entrainment of surrounding fluid. The momentum transfer between the mainstream and the surrounding fluid can form the velocity gradient and the shear stress in the mixing layer, and thus resulting in some changes of flow structure. For example, the cross-sectional area is expanded, the flow rate is reduced, and the flux is increased with the flow development. Therefore, the radial Mach number profile shows a typical hat-shape, revealing a narrower crown near the nozzle exit and a wider crown in the downstream. As the flow develops downstream, the Mach number on the jet axis decreases and the radial distance of the mainstream broadens meanwhile because the turbulent vortexes are fully developed by the diminution of the velocity gradient.
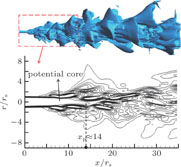
Jet half width r
0.5 is defined as the radial distance from where the streamwise velocity of the radial section is equal to half of the local maximum velocity (i.e., U
0.5 = 0.5U
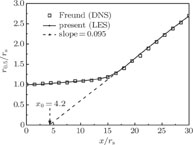
max) to the jet axis. Figure 6 shows the jet half width development on the jet axis, corresponding to the previous DNS simulation data. It can be observed that the potential core is at the distance about 14r
s away from the nozzle exit. Around the potential core is the mixing region, where the velocity difference between the mainstream and the surrounding fluid is greatest and the entrainment is the most dramatic. It is confirmed as the leading acoustic source of the turbulent jet. A virtual slash is made to denote the slope of the jet half width, and the crossing point intersected by the jet axis is about 4.2r
s, approximate to the Freund’s DNS data of 4.5r
s [31] and the Hussein’s high Reynolds number experimental value of 4.0r
s.[36] Moreover, the virtual slope of the present LES simulation is 0.095, which is located within the experimental scopes of 0.086–0.096.
Figure 7 illustrates the Reynolds stress
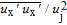 values, which are normalized by the nozzle exit velocity. In the jet streamwise direction, several lines of different locations are determined to investigate the turbulent intensities. Near the nozzle exit (i.e. x = 4.1r
s), the
values, which are normalized by the nozzle exit velocity. In the jet streamwise direction, several lines of different locations are determined to investigate the turbulent intensities. Near the nozzle exit (i.e. x = 4.1r
s), the
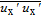 varies in a considerably tight range due to the initially laminar flow. Nevertheless, near the potential core at x = 12.5r
s, it rises rapidly to an extraordinary value of
varies in a considerably tight range due to the initially laminar flow. Nevertheless, near the potential core at x = 12.5r
s, it rises rapidly to an extraordinary value of
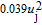 , approximate to the peak value. This remarkable phenomenon can be attributed to the rapid nonlinear saturation in this region, and an occurrence of jet flow transition. Away from the potential core,
, approximate to the peak value. This remarkable phenomenon can be attributed to the rapid nonlinear saturation in this region, and an occurrence of jet flow transition. Away from the potential core,
 decays gradually further downstream with a relatively small slope. The obtained values in the present work accord reasonably well with the numerical results by Freund though generally higher values are obtained. The differences can be attributed to the different inflow forces in the LES and DNS numerical simulations.
decays gradually further downstream with a relatively small slope. The obtained values in the present work accord reasonably well with the numerical results by Freund though generally higher values are obtained. The differences can be attributed to the different inflow forces in the LES and DNS numerical simulations.
The obtained results of single jet flow correspond to the experimental findings and the DNS data, suggesting an appropriate basis to the dual-jet flow and further acoustical computation.
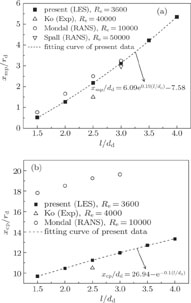
3.1.2. Noise generation and propagationWith the development of the turbulent jet, the velocity shear layer is formed at the jet boundary, leading to vortex generation due to instability. As discussed above, there is a potential core near the nozzle exit with a length of 14r
s approximately, which is manifested in the instantaneous vorticity field from Fig. 8. Surrounding the potential core, a large gradient variation of flow field is formed due to the vigorous mixing between the original jet and the entrained fluid. Therefore, a series of large-scale vortexes is generated, associated with complex and volatile stresses. As a result, the velocity and pressure in this region change rapidly with high internal stress tensor, forming a strong radiated noise. The large-scale vortexes are proved to generate stronger noise emission from previous investigations,[1,10] and the mixing region around the potential core can be predicted as a dominant acoustic source. In the transition region, the vortexes can break up and merge continuously as the motion proceeds, and large-scale vortexes gradually transform into small-scale vortexes with weaker turbulence intensities, leading to the reduction of noise emission. In the downstream of the full-developed region, the vortexes are fully developed with frequent diffusion and dissipation. Thus, the flow fluctuations and gradient variation are greatly reduced, resulting in lower levels of radiated noises. In the final analysis, the acoustic noise is formed by multi-vortex structures and the pressure fluctuations.
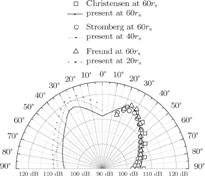
Figure 9 shows the overall sound pressure level (OASPL) distributions at the specified acoustic receivers in different directions where the noise attenuations and their directional characteristic are investigated. In the diagram, 0° represents the axial direction and 90° refers to the radial direction. The OASPL results on the arc at 60r
s are in good agreement with the previous findings.[30,31,37] The numerical results are slightly over-predicted in comparison with the experimental data due to the inaccuracy of the condenser microphone measurement. The acoustic noise radiated in the free space shows an obvious directional feature. The strongest noise emission is found at 25° with respect to the jet axis and the weakest noise is in the radial direction. The above findings can be attributed to two major factors. On the one hand, due to the jet entrainment and expansion with the flow developing downstream, the flow medium moves faster close to the central axis and slower near the jet boundary, leading to refraction effect during the noise propagation to the far-field. On the other hand, the relative movement between the acoustic source and flow field can cause the sound wave superposition like the Doppler effect: resulting in the noise directive property. Compared with the experimental data performed by Christensen et al.,[37] the radiated noise of the high Reynolds number jet exhibits the same directivity, even though the low Reynolds number jet has a more significant directive property. The OASPL distribution shows prominent noise attenuation in the propagation process. Around the potential core, a large gradient variation of flow field is formed due to complex stresses. For this reason, the pressure fluctuation on the arc at 20r
s is much more violent than that on the arc at 60r
s, forming a strong radiated noise that decays gradually in the distance.
Since the obtained findings by the developed LES/FW-H coupled method do convincingly correspond to both the representative numerical simulation results and the experimental data, this approach is considered to be an appropriate method to investigate the flow field and the acoustic noise of the dual-jet.
3.2. Dual-jet model3.2.1. Flow field and turbulence statisticsFigure 10 shows the dimensionless velocity profiles and the Reynolds stresses of different flow distances with the aperture ratio of l/dd
= 4. The statistical results are obtained by the time-averaging of the instantaneous flow fields after sufficient time to stabilize the flow in the computational domain. Near the nozzle exit, the two jets maintain their flow characteristics. Under the influence of entrainment, there is a pair of contrarotary vortices which recirculate air on the concave side of each jet. For the same reason, the streamwise velocity is negative in the region between the two jets. As a typical characteristic of dual-jet interaction, Coanda effect can be described as mutual attraction caused by entrainment. In the downstream, the mutual attraction between the two jets is significant. There is a sub-atmospheric region in the middle of the dual-jet, and the two jets have to merge together with a deflection of the jet axis. It can be seen from Fig. 10(b) that the maximum value of the Reynolds stress (
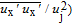 appears on the edge of the jet in the converging region in front of the merging point and the minimum value exists at the center of the jet. It is worth noting that the maximum value of the outer edge is larger than that of the inner edge of each jet. This phenomenon can be described as an influence of centrifugal force caused by the deflection of each jet. With the flow developing spatially, the inside peak of each jet diminishes progressively and vanishes further downstream.
appears on the edge of the jet in the converging region in front of the merging point and the minimum value exists at the center of the jet. It is worth noting that the maximum value of the outer edge is larger than that of the inner edge of each jet. This phenomenon can be described as an influence of centrifugal force caused by the deflection of each jet. With the flow developing spatially, the inside peak of each jet diminishes progressively and vanishes further downstream.
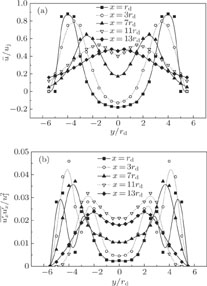
Figure 11 shows the dimensionless velocity profiles and the Reynolds stresses of different separation distances at a flow distance of x/r
d = 3. In this flow distance, the convergence of the individual jets is relatively small in order to investigate the influence of the separation distance. At a small separation distance, the interaction between the two jets is vigorous and the dual-jet behaves similar to a single jet. As l/dd
increases, the entrainment of the surrounding fluid is enhanced and the interaction between the two jets becomes weakened. As a consequence, the spread of the dual-jet in the lateral direction increases, while the relative velocity between two jets decreases. This interpretation is evidenced in Fig. 11(b) which shows the Reynolds stress distributions in the lateral direction. Due to the interaction between the two jets, the inside peak of each jet is vanished for a smaller separation distance. It can be observed that the velocity value and the Reynolds stress decrease slightly with the increase of l/dd
as a result of the entrainment and momentum transfer.
It can be ascertained from Fig. 1(b) that the merging point is an important juncture between the converging region and the merging region where the inside shear layers of the dual-jet start to join together. In the present work, the merging point is defined as a point where the mean velocity on the symmetry increases from a negative value to zero (Ū = 0). The combined point is a significant indicator suggesting that the dual-jet begins to combine together, forming a single-stream jet. Thus the combined point is identified where the two peaks of the dual-jet in the lateral direction disappear, forming a single peak. As shown in Fig. 12(a), despite various Reynolds numbers, the streamwise distance of x
mp varying with l/dd
has a similar performance to that in the previous investigations.[24,38,39] A best fitting curve of present data is established as
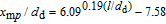 . It is noteworthy that x
mp/dd
does not increase linearly as l/dd
increases from 1.5 to 4, however, it reveals an exponential growth with small curvature. This discovery is inconsistent with the RANS results of Mondal,[24] but shows a similar variation trend to the experimental investigations (8.5 < l/dd
< 16) from Tanaka.[18] The streamwise positions of the combined points from Fig. 12(b) illustrate the exponential relationship of
. It is noteworthy that x
mp/dd
does not increase linearly as l/dd
increases from 1.5 to 4, however, it reveals an exponential growth with small curvature. This discovery is inconsistent with the RANS results of Mondal,[24] but shows a similar variation trend to the experimental investigations (8.5 < l/dd
< 16) from Tanaka.[18] The streamwise positions of the combined points from Fig. 12(b) illustrate the exponential relationship of
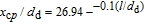 . In comparison with the RANS results of Mondal,[24] the LES results in the present work are very reasonable. This gives the credit to the capture of the multi-scale vortexes. Furthermore, the obtained results clarify that the positions of the combined point are insensitive to the Reynolds number.
. In comparison with the RANS results of Mondal,[24] the LES results in the present work are very reasonable. This gives the credit to the capture of the multi-scale vortexes. Furthermore, the obtained results clarify that the positions of the combined point are insensitive to the Reynolds number.
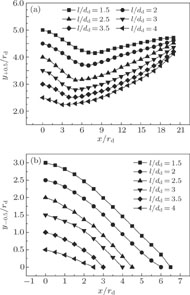
To illustrate the spatial development of the dual-jet, the comparisons between the jet half widths (y
+0.5 and y
−0.5 for different separation distances in the outer shear layer and inner shear layer are shown in Fig. 13, respectively. In the dual-jet model, the jet half width y
0.5 is defined as the lateral distance from x axis to the point where the mean streamwise velocity is equal to half the local maximum velocity (i.e., U
0.5 = 0.5U
max. Due to the mutual attraction between jet flows in the merging region, the inner jet half width y
−0.5 decreases gradually with the flow development. This can be attributed to the flow deflection caused by Coanda effect. The y
−0.5 slopes of different l/dd values imply that the streamwise direction of smaller separation distance has a relatively small deflection. The outer jet half width y
+0.5 tends to decrease first and then increase, and the minimum point appears near the merging point. The dual-jets will gradually merge together to form a single-stream jet, thus y
+0.5 increases slowly in the downstream, behaves like a single free jet as indicated in Fig. 6.
3.2.2. Effect of separation distance on acoustic propagationFigure 14 depicts the instantaneous vorticity fields of the dual-jet for the most quintessential jet separation distances of l/dd = 1.5 and l/dd = 4. Because of the mutual entrainment between the two jets, there are a large number of vortices on various scales with continuous and irregular processes (e.g. generation, development, merging and breakdown). At a smaller separation distance, the turbulence intensity is higher due to the evolution and interaction of vortex structures. Affected by the strong interaction, the two jets tend to merge together and form a single large jet. In this process, the dual-jet interaction will incur gradient variances, pressure fluctuations, and eventually increase the noise emission. The radiated noise is a synthesizing function between the superimposed noise of two jets and the additional generated noise in the merging process. This additional noise is identified as the mixing noise in the present work. Furthermore, the radiated noise generated by each independent jet is defined as the original noise, which is principally affected by the potential core. With the increase of the separation distance, the interaction between two jets gradually declines, and so does its associated additional noise. On the other hand, as discussed above, a stronger original noise will be generated by the larger potential core. As depicted in the instantaneous vorticity field of l/dd = 4, the ambient fluids between the two jets are sufficiently entrained and the vortexes of each jet are fully developed, resulting in a smaller scale of vortexes and a smaller size of potential core, which is expected to generate a smaller noise emission. When the separation distance is very small (l/dd = 1.5), the interaction between turbulent jets is greatly enhanced, leading to a larger size of potential core in each jet. What is more, a large number of large-scale vortexes are generated, which would radiate stronger acoustic noises. In summary, our numerical results predict that the dual-jet of a smaller separation distance will produce a greater noise emission.
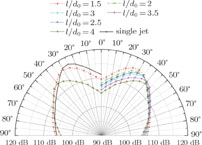
Figure 15 shows the OASPL distributions of the dual-jets in comparison with the equivalent single jet model. As depicted on the right side of the polar diagram, the global noise gradually decreases as the separation distance increases; especially near the streamwise directions from 0° to 40°. Due to smaller independent diameter of the dual-jet than that of the equivalent single jet, the sizes of the potential cores are smaller, causing less acoustic noise generation. In contrast, the interaction between two jets will enhance the additional mixing noise and sequentially increase the noise emission. Thus, the comparison between the dual-jet and the single jet on the left side of the polar diagram has great significance. It can also be found that the dual-jet noises are smaller in the overall volume, although a little larger in the lateral direction. In consequence, the potential core plays a fundamental part in the dual-jet noise emission while the effect of the mixing noise becomes relatively insignificant. This further ascertains the feasibility of noise reduction by the transformation from a single jet into an equivalent dual-jet or multi-jet. Moreover, one can also notice that it is important to select an acceptable large separation distance to avoid the additional mixing noise.
Another interesting influence of the Coanda effect on the acoustic field is the noise directive property. For a single jet, the strongest noise deviates from the streamwise direction by approximately 25°. In contrast, for the dual-jet model, the strongest noise moves to lateral direction by about 10° to 15° or even further. Compared with the equivalent single jet, the dual-jet has a discrete potential core in the upstream which can increase the vortex-induced motions in the downstream. Based on the refraction effect caused by the relative movement of flow media and the Doppler effect of acoustic wave superposition, the noise propagation tends to deflect towards the lateral direction. Furthermore, with a larger separation distance, the dual-jet exhibits a relatively weak directive property. For engineering application, the effect of the dual-jet on noise directive property can be utilized for noise control practice.
4. ConclusionsIn the present work, a three-dimensional mathematical model based on LES coupled FW-H integral equation is used to investigate the flow structure and noise propagation of the single and dual jets. The main conclusions can be drawn as follows.
(i) Based on the Coanda effect, there is a sub-atmospheric region in the middle of the dual-jet caused by the entrainment of surrounding fluids. Their interactions can bring a sequence of changes such as deflection, attraction and combination, and directly affect the flow pattern and acoustic propagation.
(ii) The LES results indicate that the positions of merging point perform exponential growth with the separation distance as
 , instead of linear relationship from the previous RANS results. It can be attributed to the accurate capture of multi-scale vortexes.
, instead of linear relationship from the previous RANS results. It can be attributed to the accurate capture of multi-scale vortexes.
(iii) The dual-jet shows a noise reduction compared with the equivalent single jet. It can be supposed that the potential core plays a fundamental role in dual-jet noise emission while the additional mixing noise makes less contribution.
(iv) In the single jet, the strongest noise is not along the axial direction, but deviates from the axial direction by about 25°. In the dual-jet, the deflection angle increases from 10° to 15
°
because of the strong interactions.
(v) The LES/FW-H coupling model is verified to be an appropriate method to investigate the flow structure and the acoustic propagation against some previous studies. Further experimental validations of the dual-jet will be performed in future work.