The electron correlation effect lies in the core of attoscience and molecular bonding, and is also important to the study of electron motion in chemical reactions. ^{[1, 2]} Double ionization of atoms in intense laser fields provides a simple electron correlation prototype and thus becomes a hot topic in the study of atom–light interaction. Studies on double ionization have revealed many electron correlation features, such as the effect of single and multiple recollisions of two electrons, the timing of electron releases in sequential double ionization, and momentum–energy redistribution among electrons. ^[1]

Nonsequential double ionization (NSDI) of noble atoms ^[3] discloses an electron correlation process during photoionization that one electron is firstly ionized by the laser field, then is driven back to its parent ion and finally knocks out another electron. Clearly, the electron correlation plays a key role in NSDI. ^{[4, 5]} Correlated-electron momentum distribution (CMD) is a principal tool to reveal the electron correlation effect in NSDI and is frequently studied. The CMD denotes the number of two electrons as a function of their momenta along the laser polarization. Many features, such as the fingerlike structure ^[6] and the cross-shape structure ^{[7, 8]} in the CMDs, are observed experimentally and analyzed theoretically. These structures bring detailed information of microscopic electronic processes. Recently, the experimentally observed transition of CMD from anticorrelation to correlation ^[9] was found to be caused by the variation of the electron correlation effect with laser intensity. ^[10]

Scaling technique is a valuable tool to analyze many physical processes and is frequently used to study the intense-laser phenomena. ^[11–15] Different from the focus on the yield variation with the laser wavelength ^{[11, 13]}, we conclude a scaling law to identify the equivalent electron processes in NSDI ^[16], by the similarity of CMDs of two electrons ionized from different atoms. The scaling law states that for two systems of laser-driven atoms S ( ) and , ), their CMDs are the same provided that we choose and , where ω and I are the frequency and intensity of the laser field, and is the second ionization potential of the atom, and the quantities with primes denote those for another system. The scaling law suggests that, under the scaling transform, the principal electronic processes of NSDI are the same, even though the laser parameters look quite different. The NSDI process can be further classified into two categories ^[17], say recollision-impact-ionization (RII) and recollision-induced excitation with subsequent ionization (RESI) processes. In the RII process, the second electron is ionized owing mainly to the electron recollision, while the second electron in the RESI process is ionized by the laser field from an excited state. Hence, the change of their CMDs with the laser field may be quite different. Do the two processes satisfy the same scaling law?

Moreover, the electron correlation is encoded directly into the CMDs of the RII electrons. This can be shown by the drift momentum that the electron obtains when it moves in the laser field. For given laser intensity and frequency, the drift momentum depends critically on the time of electron ionization, hence the drift momenta of two RII electrons are almost the same, since the two electrons were freed with a short time interval. ^[18] The first electron is ionized during the increasing edge of the electric field, and recollides with the parent core at the zero-crossing point of the electric field. ^[18] The return generally takes a half cycle, and the recollision inverses the momentum of the first electron. Consequently, the time of recollision can be regarded as the ionization time of the first electron. Hence, the drift momenta are almost the same for two electrons in the RII process. As a result, the end-of-pulse CMD of the RII electrons keeps a direct memory of the CMD at the moment of the electron collision. This presents a straightforward way to study the electron correlation in the NSDI process. According to the change of CMDs of the RII electrons, one gets the variation of the electron correlation. Because the electron correlation lies in the core of NSDI study, further study focussing on the CMDs of the RII electrons is of great importance.

In this paper, we study the CMDs of the RII electrons under the scaling transform. This paper serves two purposes. One is to show the scaling law in the RII process, the other, which is more important, is to check the change of the electron correlation under the scaling transform. For these purposes, we calculate the CMDs in the laser fields of different frequencies and intensities using a classical ensemble method. We will show that, under the scaling transform, the CMDs of the RII electrons are the same. The similarity in the CMDs indicates that equivalent electron correlations are ensured under the scaling transform.

The simulation method we employed is based on the numerical integration of the time-dependent Newton equation, which has been proved to be very effective in dealing with the NSDI phenomena. ^[19–21] This method reproduced many important features in NSDI, such as the multi-peak structure in momentum distributions of ions from single, double and multiple ionizations. ^[22], and the characteristic knee structure in the ion yield by circular polarization. ^[23] Moreover, by back-trajectory technique, this method can be used to track subcycle electronic dynamics during double ionization. ^[24–26]

The light-free Hamiltonian of a two-active-electron atom can be written as (in atomic units: a.u.):

(1)

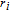
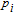
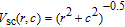
The Hamiltonian of the atom in a laser pulse is given by

(2)

In our simulations, we separate the RII from the NSDI by the time interval between the recollision time and the double ionization time. The double ionization events with the time interval less than 0.1 optical cycle are counted as the RII events, while the double ionization events with the time interval larger than 0.3 optical cycle are counted as the RESI events. By the back-trajectory technique, the contribution of the RII and RESI electrons to NSDI can be identified. Figure 1(a) depicts a CMD of two electrons from the NSDI process of the Ar atom. The CMD exhibits large cyan bright regions in the center of a blue background, and small red structures highlighted from the bright regions. The bright regions distribute mainly along the diagonal line of the plot, indicating electrons accumulated greatly in the first and the third quadrants. Figure 1(b) depicts the CMD of two electrons from the RESI process, which exhibits the bright regions along the two axes and the red structures in the central area of the plot. Figure 1(c) depicts the CMD of the RII electrons, in which the bright areas appear only in the first and the third quadrants, and the red structures keep away from the center. This demonstrates that most RII electrons are energetic and form the structures far away from the center, and that the RESI electrons form the structures nearby the center. Therefore, we focus on these energetic electrons to get deep insight into the electron correlation effect.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. (color online) CMDs of two electrons ionized from Ar atoms in laser pulse of wavelength 795 nm and intensity : (a) NSDI, (b) RESI, and (c) RII processes, and the CMD from Ne atoms in laser pulses of wavelength 536 nm and intensity (d). All the laser pulses are of 16-cycle trapezoidal shape with 3 cycles in both linear ramp on and linear ramp off.

The scaling law originates from the fact that the transition amplitude of an electron is described by Bessel functions. ^[27] It was deduced originally from single-electron photoionization of atoms. ^[28–30], and was extended to high-order harmonic generation ^[31] If we regard the two electrons in double ionization as a whole, its transition can also be described by Bessel functions. This suggests a scaling law for double ionization. Actually, the Bessel functions appear in the analytical formula of the double ionization rate. ^[32] The key of the scaling transform is to keep the ponderomotive parameter unchanged. When the laser frequency changes to , the laser intensity should be changed as , so the ponderomotive parameter defined as keeps constant. A comparison is presented in Fig. 1. The CMD shown in Fig. 1(d) is for Ne atom with k = 1.482, i.e., the ratio of the second ionization potentials. According to the bright areas and the red structures, the similarity between Fig. 1(a) and 1(d) is evident, which proves the scaling law of NSDI. This verifies that the ponderomotive parameter is a basic parameter in strong laser fields.

Does the electron correlation change under the scaling transfer? To answer this question, we study the CMDs of two RII electrons. We choose the CMD from the Ar atoms as a reference and compare the CMDs of the RII electrons under the scaling transform. Figure 2(a) depicts a CMD of two electrons from RII of the Ar atom. The bright areas locate at the first and the third quadrants. These areas are symmetrically located about the diagonal line, indicating the fact that two electrons are not distinguishable. In the first quadrant, the bright area disperses a little, hence becomes closer to the two axes. This area is not so highlighted as that in the third quadrant. This difference is caused by the ionization saturation at the leading pulse edge and becomes faint at lower laser intensities. Less electrons emit out back-to-back, hence the areas in the second and the fourth quadrants appear as a blue background. Such a distribution denotes the two electrons leaving the laser field mainly side-by-side, and is termed as correlation. This plot behaves as a reference to compare the CMDs of two electrons from other atoms.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (color online) CMDs of two electrons from RII of (a) Ar atoms in laser pulses of wavelength λ = 795 nm and intensity ; and He atoms in laser pulses of wavelength 403 nm and intensity (b), (c), and (d), respectively. The scaling ratio is 1.97.

We compare the above CMD with those from the He atoms to choose equivalent electron correlation processes in different laser fields. He atoms are a frequently studied target in NSDI. The scaling transform is featured by the cubic dependence of the laser intensity on the scaling ratio, so we compare the CMDs from the He atom driven by laser intensity , and , respectively. The scaling ratio k is chosen as the ratio of the second ionization potentials and reads 1.97, so the wavelength of the driving laser field is chosen as 403 nm. The calculated CMDs are depicted in Fig. 2(b), 2(c), and 2(d), respectively. All the CMDs exhibit the bright areas located in the first and the third quadrants, indicating the side-by-side emission being dominated. According to the bright areas and the red structures, the differences from the referential CMD are notable in the calculated CMDs shown in Fig. 2(b) and 2(d), and the similarity with the referential one is substantial in the CMD shown in Fig. 2(c). Figure 2(c) is for laser intensity of , so the similarity demonstrates the cubic dependence of the laser intensity on the scaling ratio.

For a substantial proof of the scaling law, we compare the momentum distributions of the recoil ions. The momentum distribution denotes the number of ions as a function of the recoil momentum along the laser polarization. It presents a quantitative statistic on the ions’ motion and thus provides a cross evidence to the emission of electrons. Figure 3(a) depicts the momentum distributions of the recoil ions corresponding to Fig. 2. The black line is for the Ar²⁺ ion, and the other three lines are for the He²⁺ for different laser intensities. All the lines exhibit two peaks located symmetrically about the central zero. This kind of distribution denotes that almost half of ions move in one direction and the other half of ions move in the opposite direction. Since the two electrons eject side-by-side, the recoil momentum of ion is large. The green line is for the laser intensity and agrees best with the referential line, while the red (for ) and the blue (for ) lines exhibit distinctive differences from the referential line.

Fig. 3.

Figure Option ViewDownloadNew Window

Fig. 3. (color online) Momentum distributions of the recoil ions: The black line is for Ar2+ ions produced in a laser field of wavelength λ = 795 nm and intensity , and other lines are for He2+ ions: (a) by laser fields of wavelength 403 nm and intensity (red), (green), and (blue), respectively; (b) by laser fields of wavelength λ/k and intensity for (red) and (green), respectively. For convenience of comparison, each line is normalized by its maximum, and the momentum is normalized by .

Is the ratio of the second ionization potentials the best scaling ratio? The scaling ratio is defined as the ratio of ionization potentials of two atoms, which is obvious and specific for single ionization. However, both the first and the second ionization potentials are involved in double ionization, and they combine four ratios as where i =1,2, and , where and denote the first and the second ionization potentials of one atom, and the prime denotes the other atom, respectively. The ratio is straightforward according to the energy relation in double ionization, and the ratio is meaningful if we regard double ionization as the ionization of a two-level atom. We calculate the CMDs of two electrons from RII of the He atom for different ratios. The wavelength of the laser field is chosen as λ/k and the intensity is chosen as . All the calculated CMDs exhibit two bright areas surrounded by the blue background, and the bright areas in four plots all locate at the first and the third quadrants and all keep away from the central regions. The similarity stems from the fact that the ponderomotive parameter, say , is the same in these four plots. The differences are subtle. In Figs. 4(a) and 4(b), which are for and , respectively, the bright areas in the first quadrant are larger than those in the third quadrant, and the red structures are quite dim. Those notable differences from the referential one exclude and as the best scaling ratio. The CMD shown in Fig. 4(d) is for and differs notably from the referential one, especially in the third quadrant. This indicates that is not the proper scaling ratio. However, the difference for the CMD in Fig. 4(c) from the referential one is quite subtle, hence we judge that is the best scaling ratio. For substantial proof, we compare the momentum distributions of He²⁺ ions for and with that of Ar²⁺ ions in Fig. 3(b). Distinctive differences are found for the line from the referential line, which proves again is the best scaling ratio.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. (color online) CMDs of two electrons from RII of He atoms in laser pulses of wavelength λ/k nm and intensity for different k: (a) , (b) , (c) , and (d) , respectively.

Why does the scaling ratio equal the ratio of the second ionization potentials? In double ionization, the second electron should have sufficient energy to overcome the second ionization potential for its ionization. For target atoms with larger second ionization potentials, the energy of the second electron should be enlarged in proportion. The energy of the returning electron depends on the laser intensity, and reaches a maximum of about , where is the ponderomotive energy and . During collision, the second electron shares this energy with the returning electron. So, the energy of the second electron obtained depends on the ponderomotive energy. Because the ponderomotive parameter keeps unchanged under the scaling transform, the laser frequency should be enlarged according to the ratio of the second potentials. Hence, the scaling ratio equals the ratio of the second ionization potentials. This also indicates that both the RII and the RESI processes satisfy the same scaling law as that in the NSDI process.

Using a classical ensemble method, we study the CMDs of two RII electrons that keep direct memory of the electron correlation effect. We find that the CMDs of the RII process, as well as the electron correlation effect, satisfy the same scaling law as that in the NSDI process. This indicates that the scaling law of the NSDI process is generally in the two-electron process. Under the scaling transform, many electron correlation processes, such as the energy sharing in electron-electron collision and the electron ejection from the laser field, are the same. The scaling law presents a tool to compare different colliding processes for different atoms, and a way to identify equivalent electron-electron colliding processes. We conclude that in order to get equivalent electron correlation effects, one should choose laser fields of equal ponderomotive parameter, and the laser frequency should be changed in linear proportion to the second ionization potentials of the target atoms. This study presents a deep insight into the electron correlation during NSDI.