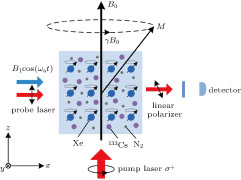
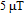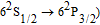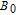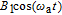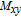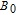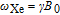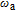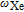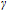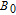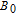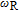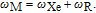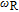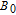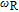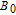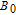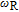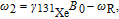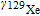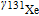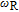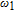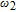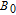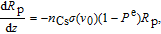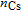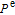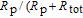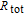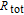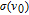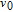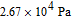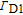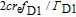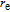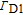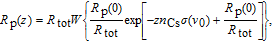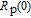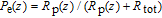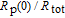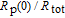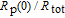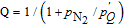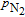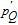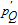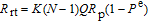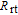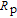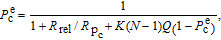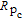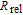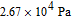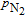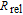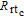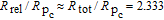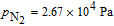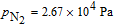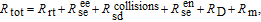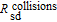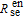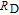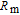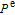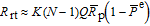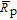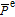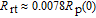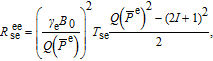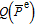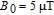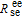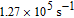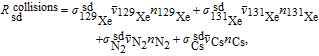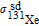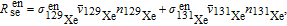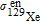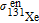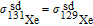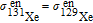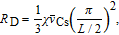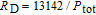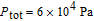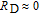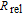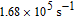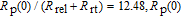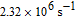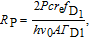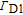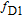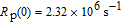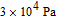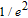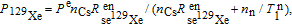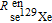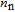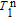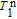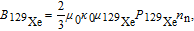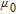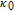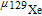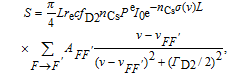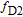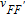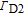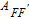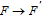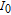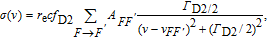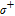2. Basic principle of NMRGThe basic principle of NMRG is illustrated in Fig. 1. The 133Cs vapor is optically pumped by a circularly-polarized laser beam [11, 12] which propagates along the z axis. A static magnetic field
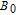 is applied along the z axis. A net electron spin polarization accumulates in 133Cs atoms. It is then transferred to Xe nuclei through spin-exchange collisions, resulting in a macroscopic nuclear spin polarization for Xe. By applying an oscillating magnetic field
is applied along the z axis. A net electron spin polarization accumulates in 133Cs atoms. It is then transferred to Xe nuclei through spin-exchange collisions, resulting in a macroscopic nuclear spin polarization for Xe. By applying an oscillating magnetic field
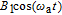 along the x axis, the Xe spin magnetic moment M tilts from the z axis, and its component along the xy plane
along the x axis, the Xe spin magnetic moment M tilts from the z axis, and its component along the xy plane
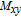 will precess about
will precess about
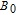 with an angular frequency
with an angular frequency
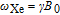 , where
, where
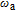 approximately equals to
approximately equals to
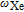 and the proportional constant
and the proportional constant
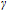 is the gyromagnetic ratio of Xe. The 133Cs spins precess about the total magnetic field, which is the sum of
is the gyromagnetic ratio of Xe. The 133Cs spins precess about the total magnetic field, which is the sum of
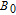 and the Xe spins generated part. Since the alkali-metal atoms are more susceptible to the magnetic field than the noble gas [13], a linearly-polarized probe laser beam whose frequency is near resonant with the 133Cs optical transition may rotate its polarization of the macroscopic field component along the x axis of the polarized Xe atoms precess about
and the Xe spins generated part. Since the alkali-metal atoms are more susceptible to the magnetic field than the noble gas [13], a linearly-polarized probe laser beam whose frequency is near resonant with the 133Cs optical transition may rotate its polarization of the macroscopic field component along the x axis of the polarized Xe atoms precess about
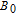 field, the photoelectric detector accepted laser intensity will periodically vary after the probe laser passes through the linear polarizer. Assuming the gyroscope is rotating about the z axis at a frequency
field, the photoelectric detector accepted laser intensity will periodically vary after the probe laser passes through the linear polarizer. Assuming the gyroscope is rotating about the z axis at a frequency
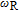 , the measured Larmor precession frequency will change from the reference
, the measured Larmor precession frequency will change from the reference
 to be
to be
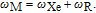 | (1) |
To determine
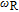 , precise knowledge and careful control of
, precise knowledge and careful control of
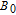 are needed. A two-NMR-isotope method fundamentally uncouples
are needed. A two-NMR-isotope method fundamentally uncouples
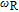 from
from
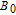 , reducing the difficulty in stabilizing
, reducing the difficulty in stabilizing
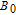 . To this end, both 129Xe and 131Xe are contained in the vapor cell which means they have the same
. To this end, both 129Xe and 131Xe are contained in the vapor cell which means they have the same
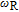 . Since γ of 129Xe and 131Xe have different values and opposite signs, they have their respective precession frequencies [14]
. Since γ of 129Xe and 131Xe have different values and opposite signs, they have their respective precession frequencies [14]
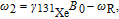 | (2) |
where
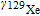
and
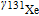
are gyromagnetic ratios of
129Xe and
131Xe. Therefore,
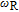
can be deduced by simultaneously monitoring
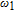
and
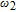
, where
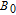
is seen as a removable common-mode parameter and
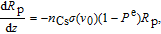 | (3) |
where
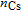
denotes the cesium atomic density, the normalized polarization
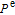
is the
133Cs polarization and defined as
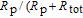
) with
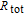
being the total spin-relaxation rate, here we consider
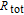
as a fixed value, and
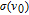
is the photon absorption cross-section at the resonance frequency
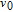
. For the D1 line of
133Cs, the linewidths broadened by the
129Xe/
131Xe and N
2 (for
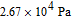
) pressures are 6 GHz and 6.8 GHz
[20] respectively for mixture II. For comparison, the natural linewidth is 4.6 MHz and the Doppler broadening linewidth is 427 MHz. Thus
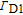
is dominated by the pressure broadening,

approximately equals to
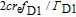
, where
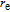
is the classical electron radius,
c is the speed of light,

is the D1 transition oscillator strength, and
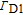
is the transition linewidth.
The principal value of the Lambert W-function (the inverse of the function
 ) describes the solution of Eq. (3), which is given by
) describes the solution of Eq. (3), which is given by
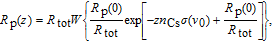 | (4) |
where
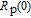
is the pump rate at
z = 0, i.e., at the front of the cell. The
133Cs polarization
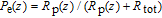
, we perform the
133Cs polarization as a function of different
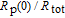
conditions at the center of the cell, as shown in Fig.
2. When the pump rate is comparable to the total spin-relation rate, the polarization is small. When the pump rate is much higher than the total spin-relation rate, the polarization rapidly increases first and then slowly increases. In NMRG, obtaining high polarization of
133Cs is difficult and the obtainable highest
133Cs polarization is about 20% at present.
[15] Here we will discuss the relevant parameter to achieve 30%
133Cs polarization. In order to obtain 30%
133Cs polarization at the cell center, from Fig.
2 we know
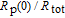
should be controlled around 12.48 by adjusting the pump laser intensity.
A phenomenon known as radiation trapping may degrade the polarization of the alkali vapor. Radiation trapping happens when the unpolarized photons scattered by excited 133Cs atoms through spontaneous emission are reabsorbed by other adjacent atoms. In our case, a quenching gas N2 [11, 12] is added to it to create a pathway for the atoms to decay to the ground state without emitting photons at all. The fraction of atoms that reach the ground state by emitting a photon rather than quenching is given by
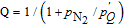 , where
, where
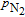 is the N2 pressure, and
is the N2 pressure, and
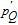 is a characteristic pressure. For the D1 line of 133Cs at 110 °C,
is a characteristic pressure. For the D1 line of 133Cs at 110 °C,
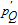 is 473 Pa.[22] The spin-relaxation rate due to radiation trapping is
is 473 Pa.[22] The spin-relaxation rate due to radiation trapping is
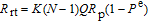 , where K describes the degree of depolarization caused by reabsorbing a photon, N is the average number of times that a photon is emitted before it leaves the vapor cell. Note that
, where K describes the degree of depolarization caused by reabsorbing a photon, N is the average number of times that a photon is emitted before it leaves the vapor cell. Note that
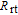 is proportion to
is proportion to
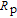 , so the radiation trapping effect is also location-dependent. In the presence of the quenching gas, the obtainable 133Cs polarization at the cell center is
, so the radiation trapping effect is also location-dependent. In the presence of the quenching gas, the obtainable 133Cs polarization at the cell center is
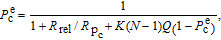 | (5) |
where
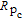
is the pump rate at the center of the cell and
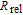
is the relaxation rate due to effects other than radiation trapping.
K is always below 1 due to uncompleted depolarization. In theory, a reasonable value of
K is 0.06 according to Ref. [
22] and
N is calculated about 75 for mixture II when N
2 pressure is
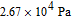
.
[23] In fact, when
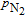
is set to be dozens of Torr (1 Torr = 1.33322×10
2 Pa),
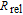
will be much larger than
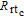
, which means the polarization is not mainly limited by the radiation trapping.
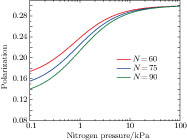
Figure 3 shows the 133Cs polarization at the center of the cell as a function of N2 pressure with N around 75 when assuming
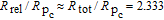 . The figure indicates that the polarization will keep growing until saturation as the N2 pressure increases. It shows that at the cell center 133Cs polarizability is about 29.5% (less than 30%) when
. The figure indicates that the polarization will keep growing until saturation as the N2 pressure increases. It shows that at the cell center 133Cs polarizability is about 29.5% (less than 30%) when
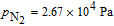 , which indicates that the radiation trapping cannot be ignored. Meanwhile, the similar tendency of three lines suggests that the polarization is insensitive to N when
, which indicates that the radiation trapping cannot be ignored. Meanwhile, the similar tendency of three lines suggests that the polarization is insensitive to N when
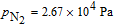 , which means that the 133Cs polarization is stable when various errors are taken into consideration in this regime.
, which means that the 133Cs polarization is stable when various errors are taken into consideration in this regime.
Apart from the radiation trapping, several other effects contribute to the total relaxation rate, which is given by
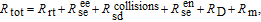 | (6) |
where

is the Cs–Cs spin-exchange collisional term,
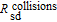
is the spin-destruction collisional term,
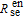
is the Cs–Xe spin-exchange collisional term,
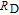
is the term of diffusion to the walls, and
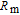
is the probe laser pumping term.
As aforementioned, the spin-relaxation rate due to radiation trapping is related to
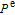 , which is nonuniform throughout the cell, here we assume
, which is nonuniform throughout the cell, here we assume
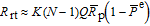 ,
,
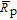 and
and
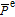 are the mean pump rate and mean polarizability from z = 0 to the cell center respectively, thus
are the mean pump rate and mean polarizability from z = 0 to the cell center respectively, thus
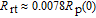 . In actual experiments, the probe laser frequency is tuned far from resonance and the laser power is usually relatively low. Therefore, the probe laser pumping term
. In actual experiments, the probe laser frequency is tuned far from resonance and the laser power is usually relatively low. Therefore, the probe laser pumping term
 can also be ignored. Spin-exchange collisions between alkali metal atoms are very fast and
can also be ignored. Spin-exchange collisions between alkali metal atoms are very fast and
 can be estimated as [24]
can be estimated as [24]
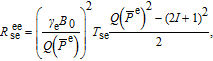 | (7) |
where
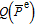
is the slowing down factor,

denotes the spin-exchange rate,

is the gyromagnetic ratio of
133Cs, and
I is
133Cs nuclear spin. In the magnetic field
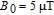
,
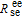
is calculated to be
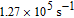
. The relaxation term of spin-destruction collisions between
133Cs and other elements in the cell is
[7]
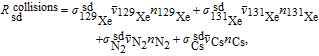 | (8) |
where

,
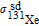
,

, and

are spin-destruction cross-sections of Cs–
129Xe, Cs–
131Xe, Cs–N
2, and Cs–Cs collisions respectively, and

represents the mean velocity. The relaxation rate due to spin-exchange collisions between
133Cs atoms and the NMR medium Xe is
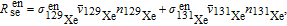 | (9) |
where
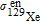
,
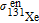
are spin-exchange cross-sections of Cs–
129Xe, Cs–
131Xe. Here we approximate
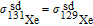
and
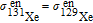
to calculate the relaxation rates in Eq. (
8) and Eq. (
9). When an alkali atom encounters the glass surface of the cell wall, it will experience the large local electric and magnetic fields produced by ions and molecules within the glass. The polarized spins undergo a depolarization process with a rate
[22–25]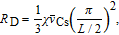 | (10) |
where
χ is a diffusion constant. Equation (
10) may be written in terms of the total pressure
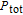
as
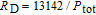
. For
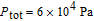
,
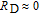
. The relaxation rate
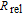
is
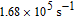
. Together with the result of
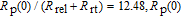
turns out to be
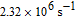
.
Now we come to estimate the pumping laser intensity. According to the pumping scheme shown in Fig. 1, the optical pumping rate can be expressed as
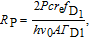 | (11) |
where
P is the pump laser power,
h is the Planck constant, and
A is the pump laser facula area,
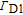
is the broadening linewidth of the D1 line, and
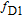
is the D1 transition oscillator strength of
133Cs. To meet the requirement of
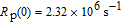
, the pumping laser intensity
P/
A is calculated to be 1171 mW/cm
2. In this way, we discuss the pump laser intensity of the three kinds of gas mixture with different N
2 pressures to achieve 30%
133Cs polarization at the center of the cell, which is shown in Fig.
4. The pump intensity drops sharply at first then slowly rises. The minimum intensity of mixture I, mixture II and mixture III are 1020 mW/cm
2, 1169 mW/cm
2, and 1371 mW/cm
2 when the N
2 pressure is about
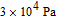
, higher
129Xe/
131Xe pressure corresponding to higher minimum pump laser intensity to achieve the same
133Cs polarization. At present we have developed a Distributed Bragg Reflector (DBR) diode-laser
[26] at 895 nm. The laser optical fiber coupling power output exceeds 60 mW. For this purpose, the laser
beam diameter could be expanded to 3.87 mm, 3.62 mm, and 3.34 mm for mixture I, mixture II, and mixture III respectively.
The net polarization of 133Cs atoms is transferred to 129Xe/131Xe atoms through spin-exchange collisions. To obtain the same macroscopic nuclear magnetic moment, the pressure ratio of 129Xe and 131Xe has been set to 1:4 [16] throughout our discussions. The polarization of 129Xe can be estimated as
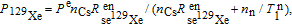 | (12) |
where
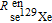
is the
133Cs–
129Xe spin-exchange rate,
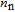
is the
129Xe atomic density, and
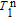
is the longitudinal spin relaxation time of
129Xe.
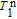
can reach about 20 s even without anti-relaxation coating of the cell wall. By applying a specified oscillating magnetic field perpendicular to
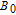
, the Xe spins will precess about the
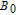
direction, generating a precessing macroscopic magnetic field. The magnitude of the macroscopic magnetic field has an important influence on the detected signal and can be expressed as
[27]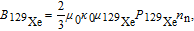 | (13) |
where
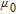
is the vacuum permeability,
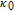
is the enhancement factor of the Cs–
129Xe interaction, and
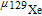
is the
129Xe nuclear magnetic moment. The effective field sensed by
133Cs due to polarized
129Xe or
131Xe magnetization is about 181 nT, 302 nT, and 484 nT for mixture I, mixture II, and mixture III respectively.
Since alkali metal atoms are very sensitive to the magnetic field, the Larmor precession frequencies of 129Xe and 131Xe can be measured by using the polarized 133Cs atoms. An off-resonance linearly-polarized probe laser beam will rotate its polarization when it interacts with the polarized 133Cs, which is known as the Faraday rotation effect. As shown in Fig. 1, the probe beam propagates along the x-axis, which is orthogonal to the pump beam. The detected rotation signal is given by [22]
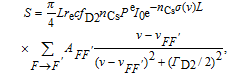 | (14) |
where
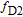
is the D2 transition oscillator strength of
133Cs,
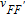
and
v are the
133Cs D2 hyperfine transitions resonance frequency and the probe laser frequency respectively,
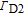
is the broadening linewidth of the D2 line,
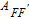
is the relative strength of the hyperfine transition
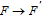
, and
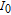
is the probe laser intensity. From Eq. (
14), we know that the probe laser intensity is proportional to the detect signal and it does not affect the optimal probe laser frequency detuning. The photon absorption cross section of cesium is written by
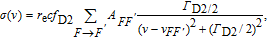 | (15) |
which contains the overall contributions of the D2 line hyperfine transitions. The dependences of the optical rotation signal on the probe laser detuning of the three types of
129Xe/
131Xe mixtures are shown in Fig.
5. The signals are somewhat like the dispersion shaped type. The differences are that there are little optical rotations around the resonant frequency. The maximum rotation signals are obtained when the probe laser frequencies are 92 GHz, 106 GHz, and 124 GHz for mixture I, mixture II, and mixture III detuning from the D2 resonance.