† Corresponding author. E-mail:
The magnetic behaviors of the Fe–Mn–Al alloy are simulated on the Bethe lattice by using a trimodal random bilinear exchange interaction (J) distribution in the Blume–Capel (BC) model. Ferromagnetic (J > 0) or antiferromagnetic (J < 0) bonds or dilution of the bonds (J = 0) are assumed between the atoms with some probabilities. It is found that the second- or the first-order phase boundaries separate the ferromagnetic (F), antiferromagnetic (AF), paramagnetic (P), or spin-glass (SG) phases from the possible other one. In addition to the tricritical points, the special points at which the second- and the first-order and the spin-glass phase lines meet are also found. Very rich phase diagrams in agreement with the literature are obtained.
After the introduction of the Blume–Capel (BC) model[1,2] in 1966 as a spin-1 model, it has evolved to many different forms to investigate the magnetic behaviors of various materials. These materials may consist of atoms which may prefer to bond ferromagnetically, antiferromagnetically or not bond at all. The Fe–Mn–Al alloy is such a material where the aluminum atoms behave as magnetic holes responsible for the dilution effects, while the iron and manganese atoms play the role of magnetic sites.[3–8]
A quenched disordered Ising model with a distribution function that includes dilution and random bonds, ferromagnetic or antiferromagnetic, was studied through the mean-field renormalization-group approach[4] with only J in the Hamiltonian. In a similar work, the probability distribution was altered by adding an extra competing random bond term and the critical temperature against ferromagnetic bond concentration phase diagrams, which were analyzed for several values of the theoretical parameters.[5] By using the variational principle for the Gibbs free energy based on the Bogoliubov inequality, the magnetic properties of disordered systems with competing interactions were studied with the emphasis made to the ternary system Fe–Mn–Al.[7] A random-bond BC model was proposed to study the ternary Fe–Ni–Mn and Fe–Al–Mn alloys by using the extended mean-field renormalization group approach and a variational procedure based on Bogoliubov inequality for the free energy in the pair approximation.[8] The spin-glass BC model was studied by using an extended mean-field renormalization group approximation by a probability distribution of the bilinear interaction coupling with competing interactions to investigate the different phase regions of the model.[3] As an experimental work, the melted alloys of the FexMn0.65−xAl0.35 disordered system, 0.25≤ x ≤0.65, were studied by Mössbauer spectrometry, vibrating sample magnetometry, and AC magnetic susceptibility.[6] As seen from the above references, mostly the mean-field renormalization-group approach was used in addition to the work with variational principle for the Gibbs free energy based on the Bogoliubov inequality.
In this work, the trimodal random distribution of the bilinear exchange interaction is considered in the BC model by giving special attention to ternary alloy consisting of Fe, Mn and Al. The model is simulated on the Bethe lattice (BL) and exact recursion relations (ERR) are employed to calculate the order-parameters and free energy of the model.[9–11] The thermal variations of the order-parameter and free energy are studied numerically to obtain the phase diagrams on the possible planes spanned by our thermodynamic system parameters. It is found that our model presents either one of the phases F, AF, SG, and P depending on the values of system parameters. The phase boundaries separating the possible combinations of these phase regions are either the lines second-order phase transitions or first-order phase transitions. In addition to the tricritical points (TCP) at which second- and first-order phase transition lines combine, a special point, where the second-, first-, and spin-glass phase lines combine, is also found. It is also found that our results are in agreement with the given references.
A fictitious lattice, i.e., a BL, is considered in here to study our model instead of a real lattice. Sometimes, the exact solutions for the realistic systems on regular lattices may not be available or may be very difficult to study, therefore, one usually relies on approximation methods to obtain at least a qualitative picture of the considered system. Thus, a lattice-like fictitious tree may be introduced to find exact or approximate solutions of the model. Historically, the BL gets its name from the fact that its partition function is exactly that of an Ising model in the Bethe approximation. The BL calculations provide exact solutions and its results are qualitatively better approximations for regular lattices than solutions obtained by the conventional mean-field theories.[12] In addition, the cluster variation method in the pair approximation studies on regular lattices yield results that are exact for the same model on the BL.[13–15] It can also be adapted very easily for different types of systems, therefore, it provides a wonderful tool for the study of interesting spin models.
The rest of the work is set up as follows: Section
The well-known Hamiltonian for the spin-1 atoms is given in the BC model as
 | (1) |
A trimodal random bilinear exchange interaction is assumed for the parameter Jij as
 | (2) |
In this work, instead of using real lattices to simulate the model, a fictitious lattice, i.e., BL, is used. A BL is an infinite Cayley or regular tree, a connected graph without circuits, has been widely used in solid state and statistical physics; it is a wonderful tool easy to adapt to different problems and its results are exact. It consists of a central spin σ0, which may be called the first generation spin. σ0 has z NN, i.e., the coordination number, which forms the second generation spins σ1. Each spin in the second generation is joined to (z − 1) NN’s. Therefore, in total, the second generation has [z(z − 1)] NN’s which form the third generation spins σ2 and so on to infinity. Each generation of spins is called the shells of the BL and the number of generations goes to infinity in the thermodynamic limit.
One approach to the problem is to start with a partition function which is given as
 | (2) |
The next step is to calculate the ERR’s on the BL which was already carried out in a few works.[11,17,18] Thus we do not intend in here to obtain the whole formulation of our model but only give the necessary equations. The ERR’s are given as the ratios of partial partition functions, gn, and are calculated as follows:
 | (4) |
 | (5) |
The general procedure for the calculation of the spin system with AF interactions requires the BL to be partitioned into two sublattices A and B which does not modify the results for the F case but it is necessary for the AF case. Thus, the recursion relations for the sublattices A and B are given in the form
 | (6) |
The order-parameters for the sublattices can easily be obtained in terms of the ERR’s. It should be mentioned that all the sites deep inside the BL are equivalent, therefore, one can pick a central spin, σ0, and calculate its order parameters. The magnetization or dipolar moment for sublattice A is given as
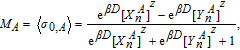 | (7) |
 | (8) |
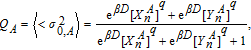 | (9) |
 | (10) |
As the last equation, one may also need the free energy of the system in terms of ERR’s to classify the type of phase transitions, i.e., whether it is the second- or the first-order, which is calculated as
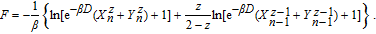 | (11) |
In the next section, the thermal variations of the order-parameters are studied to obtain the phase diagrams on the possible planes of the thermodynamic parameters. Whenever it is necessary, the temperature variation of free energy is also studied. In order to obtain the thermal behaviors of the order-parameters, i.e. the dipolar and quadrupolar moments, first the recursion relations are calculated by using an iteration scheme, then the found values of the recursion relations are inserted into the definitions of the order-parameters to obtain their thermal variations for given D, p, x, q when z = 8 and α = 1.0. In the next section, we illustrate our results, try to explain their meanings and give comparisons whenever possible.
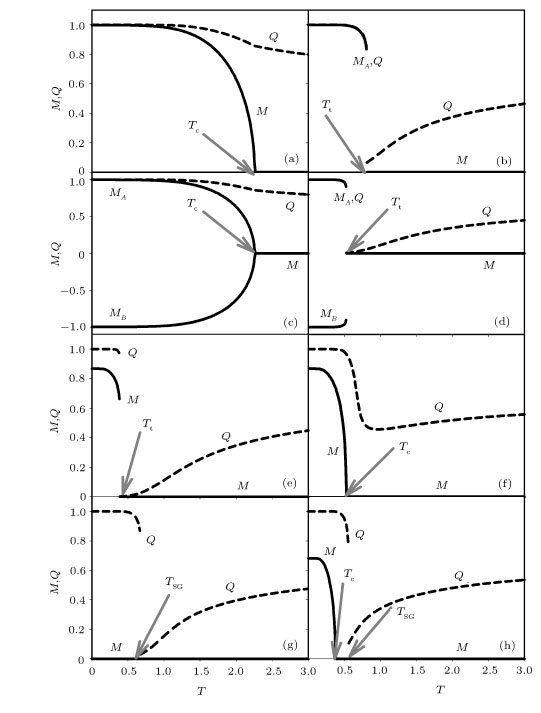
First, the thermal changes of the order-parameters are illustrated in Fig.
The phase diagrams are the collection of critical points, Tc, Tt, and TSG, obtained from the thermal analysis of order-parameters. In the phase diagrams, the solid, dashed, and dotted–dashed lines correspond to the Tc, Tt, and TSG lines, respectively. The filled circles indicate the places of TCP’s at which the Tc and Tt lines combine. The filled rectangles show the places of special points at which Tc, Tt, and TSG lines combine. The calculations are carried out on fcc lattices, i.e., z = 8, and the symmetric case of F and AF interactions are considered, i.e., α = 1.0. Thus, we are left with the parameters: temperature (T), crystal field (D), probability of bonding ferromagnetically or concentration of Fe atoms (p), probability of bonding antiferromagnetically or concentration of Mn atoms (x), and probability of bond dilution or concentration of Al atoms (q). Thus, the possible phase diagrams of the model can be obtained on a two-dimensional plane: one of the axes being the temperature and the other one is chosen to be one of these four parameters.
Figures
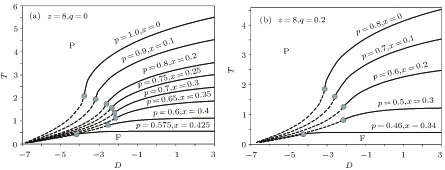 | Fig. 2. The phase diagrams on the (D,T) planes for α = 1.0, z = 8 and given values of p when (a) q = 0.0 and (b) 0.2. |
 | Fig. 3. The phase diagrams on the (D,T) planes for α = 1.0, z = 8 and given values of p when (a) x = 0.0 and (b) 0.2. |
The next phase diagrams, figures
 | Fig. 4. The phase diagrams on the (x,T) planes for α = 1.0, z = 8 and given values of D when (a) q = 0.2 and (b) q = 0.4. |
Figures
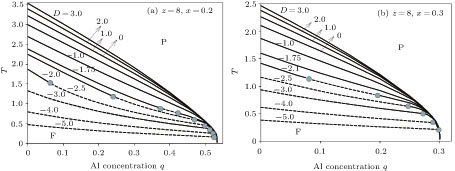 | Fig. 5. The phase diagrams on the (q,T) planes for α = 1.0, z = 8 and given values of D when (a) x = 0.2 and (b) x = 0.3. |
The spin glass phase appears only in the next phase diagrams, which are obtained on the (p,T) planes when q = 0, 0.05, 0.1, and 0.2, as shown in Fig.
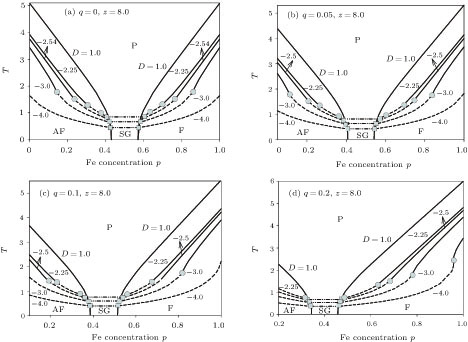 | Fig. 6. The phase diagrams on the (p,T) planes for α = 1.0, z = 8 and given values of D when (a) q = 0.0, (b) q = 0.05, (c) q = 0.1, and (d) q = 0.2. |
We can summarize our findings as follows.
As q increases, i.e., Al concentration, the critical temperatures decrease. As x increases, i.e., Mn concentration, the critical temperatures decrease again since the sublattice magnetizations have different signs. When p, Fe concentration, is increased, the critical temperatures go up. At higher D’s only Tc’s, at mid-values of D’s two TCP’s and for higher negative D’s only a TCP for each D are seen for the phase diagrams on the (q,T)- and (x,T)-planes. The SG phase is only found for the phase diagrams on the (p,T) planes which are only seen for lower negative D values. As soon as bond dilution, i.e., Al, is introduced, the symmetry is spoiled in the (p,T) phase diagrams. Our obtained critical values of the parameters q and x are a little higher than the ones obtained in Ref. [3].
As a last word, we should say that even if we did not introduce any spin glass order parameters, we were able to obtain the SG phase just by investigating the thermal behaviors of the order-parameters as indicated in Figs.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] |