† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 61505261 and 11304397) and the National Basic Research Program of China (Grant No. 2013CB338002)
Recently, a round-robin differential phase-shift (RRDPS) protocol was proposed [Nature
Quantum key distribution (QKD) allows two legitimate parties (typically called Alice and Bob) to generate a common string of secret key bits in the presence of eavesdroppers. In principle, the laws of quantum mechanics guarantee the unconditional security of QKD.[1, 2] Since the Bennett–Brassard 1984 (BB84) protocol was proposed in 1984,[3] QKD has attracted public attention and many protocols are presented for both discrete variable[4–10] and continuous variable.[11, 12] In most protocols, the information leakage of quantum communication needs to be estimated by monitoring signal disturbance, which sacrifices signals for sampling and decreases the efficiency of the protocols.
Different from many protocols such as BB84, a new approach named round-robin differential phase-shift (RRDPS) quantum key distribution was proposed.[13] It has attracted intensive attention from theoretical works[14–16] and has been implemented in optical fibers using readily available optical telecommunication tools.[17–20] Due to its distinctive measurement scheme, privacy amplification of this protocol depends on the states preparation instead of the signal disturbance. This property causes the protocol to have a better tolerance of bit errors and finite-length effects. Furthermore, there is an obvious indication that RRDPS is largely insensitive to multiphoton states. This protocol allows communication parties to transmit much brighter states obtaining higher communication rates and longer distance.
Inheriting the benefit of the RRDPS protocol, we introduce the states of PE-BB84 into the RRDPS protocol, where each pulse is randomly phase modulated by one of {0, π/2, π, 3π/2}. We call it the round-robin differential quadrature phase-shift (RRDQPS) QKD. Combining the superiorities of BB84 and the RRDPS protocol, the security of this scheme is based on the fact that a secure key can be obtained only when the basis of the signal state matches that of the measurement system, in addition to measuring the phase difference between pulses at different intervals in a packet. The RRDQPS protocol can be implemented with essential similar hardware to the PE-BB84 except adding a variable optical delay line.
The most general attacks in QKD are coherent and joint attacks, in which Eve treats the entire key as a system and utilizes the information leaked in error correction and privacy amplification. Needing a probe of large dimensionality with infinite coherence time, these attacks are beyond the domain of the current technology. In addition, the proof of security against coherent attacks may be quite difficult, one can restrict eavesdropping to individual attacks, in which Eve entangles each photon with an independent probe and measures these probes independently. The restriction to individual attacks is regarded as a practical assumption for the foreseeable future.
This paper is organized as follows. In Section
In round-robin differential quadrature phase-shift (RRDQPS) quantum key distribution protocol, we employ a train of pulses with block-wise phase randomization and utilize the relative phases between two pulses of the packet. Since secret keys are encoded on pairs of pulses and the whole train of pulses is linked together by the phase relations, it is no use for eavesdroppers to work on each pulse separately. Despite this notable simplicity in the implementation, because of the non-deterministic collapse of a wavefunction in a quantum measurement, it has been expected that the protocol should be robust against many strong attacks by eavesdroppers, including photon-number-splitting (PNS) attacks and intercept-and-resend (IR) attack.
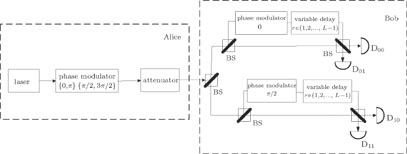
Figure
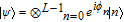 |
In detail, when the phase difference sent from Alice ΔθA ∈ {0, π} and the phase shift in Bob is 0, Alice creates bit “0” from ΔθA = 0 and creates bit “1” from ΔθA = π, then Bob creates bit “0” from the click of D0 and bit “1” from the click of D1. When ΔθA ∈ {π/2, 3π/2} and phase shift is π/2, Alice creates bit “0” from ΔθA = π/2 and creates bit “1” from ΔθA = 3π/2. Then Bob creates bit “0” from the click of D0 and bit “1” from the click of D1. If the phase shift of Bob mismatches the phase difference in Alice, they discard the data.
Obviously, the model of the RRDQPS protocol can be considered containing two RRDPS measurements, as shown in Fig.
Here we consider equivalent ways of carrying out the RRDQPS protocol.[21]
(i) Alice prepares L auxiliary qubits and L optical pulses in state
 |
where b corresponds to the choice of basis, while ak refers to a random bit. She measures, v, the total number of photons in the L pulses with projective measurement, and sends the encoded state to Bob.
(ii) Bob utilizes the beam splitter and interferometers, records the pair of valid timing {k,k + r} and announces it through the public channel.
(iii) Alice operates a CNOT gate on the k-th qubit, as the control qubit, and the (k + r)-th qubit, as the target one.
(iv) Alice measures all the qubits but the (k + r)-th one on X basis 

(v) Alice and Bob repeat the above steps to accumulate enough raw keys.
(vi) After a sifting step, Alice and Bob share the sifted key bit. Then they conduct error correction and privacy amplification to extract the final key.
Since a CNOT gate on Z basis can be seen as a CNOT gate on X basis exchanging the target and control qubits, the alternative protocol measures all L qubits on X basis to obtain L bits and calculate the sk ⊕ sk + r. This shows that the alternative protocol is identical to the previous one from the view of Eve.
In this section, we consider some typical attacks that Eve might perform. Two basic attacks including intercept-resend attack and beam-splitting attack are shown. Analyzing the performance of the protocol against these attacks in detail, we obtain an intuitive idea of the security of the protocol.
An intercept-resend attack is a typical individual attack, where the eavesdropper, Eve, cuts into the line, using the same apparatus as Bob. Eve measures the whole pulse train and resends a fake state to Bob according to her measurement result. Figure
The periodic train of attenuated laser pulses is sent out by Alice then received by Bob or Eve. Randomly choosing a variable delay for each packet, Bob or Eve measures the packet using an unbalance interferometer. We discuss what happens when Bob and Eve choose the same delay, and the probability of this case is 1/(L−1). Without loss of generality, we assume that the phase difference of the valid pulses in Alice is 0. When Eve measures the packet with a Mach–Zehnder interferometer having a phase shift of 0, detector D0 will click. When Eve measures with an interferometer having a phase shift of π/2, the probability of the detection at D0 or D1 is equal to 50%. In other words, from the detection of D0, Eve cannot judge the differential phase Δθ = 0,π/2 or 3π/2. What she can do is randomly resend fake states with one of these phase differences to be 0,π/2 or 3π/2, where the possibilities are 0.5, 0.25 and 0.25 respectively. Taking the first row for example, the probability of Eve choosing “0” is 1/2 and D0 is certain to click. Then the probability of Bob choosing “0” is also 1/2. Thus, the ultimate probability of this case is 1/2 × 1/2 = 1/4. For the resent states, since Alice and Bob create a key bit only when their basis choices are matched, the possibility of the key generation is shown as Table
| Table 1 The intercept-resend attack when Alice sends θθA=0, Bob and Eve choose the same delay. In the second to the fourth column, the basis choices of Eve, the measurement results and the phase differences resent by Eve are given. The next columns contain the basis chosen by Bob and the detection results. In the last two columns, the results of sifting and corresponding probabilities are given. . |
It is also easy to see from Table 

The basic idea behind the second attack strategy is shown in Fig.
The amount of information Eve obtains per packet depends on the transmission between Alice and Bob η and the average photon number per packet Lμ, where L is the length of each packet. In each packet containing L pulses, Eve transmits Lημ photons to Bob and stores L(1 − η)μ photons. After knowing the information of Bob, Eve delays her measurement and the probability of click from the packet is 2(1 − η)μ, which can be considered as the information Eve obtains.
In RRDQPS, the amount of information leakage can be seen as a function of average photon number. Optimizing the choice of μ can decrease the information leakage and remove it by privacy amplification, indicating the robustness of the protocol against the beam-splitting attack. As for the photon-number-splitting (PNS) attack, it breaks the coherency of the pulses in a packet, then it will reveal the existence of the eavesdropper. The RRDQPS protocol can effectively be robust against photon-number-splitting attack.
In this paper, a new quantum key distribution protocol named round-robin differential quadrature phase-shift (RRDQPS) QKD has been proposed. A coherent pulse train phase modulated by {0, π/2,;π/3 π/2}, for each pulse is transmitted and measured with a Mach–Zehnder interferometer having a phase basis of 0 or π/2. The RRDQPS protocol can be implemented with essential similar hardware to the PE-BB84, so it has great compatibility with an existing system. After describing the setup and procedure of this protocol in detail, we analyze the security of the protocol against the intercept-resend attack and the beam-splitting attack. There is a long way to go for strict proof of the security of the protocol, but we anticipate that this kind of protocol will be an outstanding candidate for practical long distance quantum cryptography.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] |