† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11475026 and 11175023).
Enhanced electron–positron pair production by frequency chirping in one- and two-color laser pulse fields is investigated by solving the quantum Vlasov equation. A small frequency chirp shifts the momentum spectrum along the momentum axis. The positive and negative frequency chirp parameters play the same role in increasing the pair number density. The sign change of the frequency chirp parameter at the moment 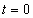
The vacuum pair production in the external electric field in the frame of quantum electrodynamics (QED) was first proposed in 1931 by Sauter[1] and also studied in 1936 by Heisenberg.[2] In particular in 1951, Schwinger studied this problem systemically by employing the proper-time technique.[3] He obtained the critical value of the constant external field to create the electron–positron (e−e+) pairs from the vacuum as 

On the other hand, because of the proposed dynamically assisted Schwinger mechanism, which combines different pulse laser fields, the vacuum pair creation may be observed even in a much lower intensity laser field.[10–15] So many ways can be used to reduce the requirement of laser field but enhance the pair production, for example, the combination of sinusoid/ cosine with exponential laser pulse,[16–18] by using super-Gaussian instead of Gaussian pulse to widen pulse width,[19,20] the usages of multi-slit interference due to the alternating sign N-pulse electric fields or/and polarized field,[21–23] and so on.
Beside changing the shape or carrier phase,[16,19] it is also expected and found that, through adding a small frequency chirping, it can influence the momentum distribution and then possibly increase the created e−e+ pair number density.[24,25] In Ref. [24], different frequency chirps lead to the changing of the momentum spectra and it is explained by a turning point. In our previous work,[25] the field time was divided into three parts and different frequency chirps are applied. Also in our work of Ref. [26] we have gained the enhanced electron–positron pair production of a vacuum in a strong laser pulse field by the possible irregular frequency variation. These few researches make this topic very interesting meanwhile leaving some problems still open. For example, whether the momentum spectra and pair number are dependent on the sign of frequency chirping? What phenomena occur if we change the one-color pulse with single frequency chirping to a two-color pulse with double frequencies chirping or if we change the sign of chirp parameter from positive (negative) to negative (positive) at the peak position of one-color laser pulse? How the two-color laser pulse field with different chirping affect the momentum spectra and the pair production rate?
In this paper, we will answer these questions. We have studied the one-color and two-color laser pulse fields by adding positive or negative frequency chirp parameters and analyze the effects of the frequency chirp parameters on the laser pulse shape, momentum spectrum and number density. It is found that a small frequency chirp can shift the momentum spectrum along the momentum axis. The positive and negative frequency chirp parameters play the same role in increasing the pair number density. The sign change of frequency chirp parameter at the moment 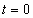

For the completeness of the paper, we have to include the description about the basic ideas and formula of the quantum Vlasov equation while the content would be unavoidable repetition of other published papers. Here we outline it similar to Ref. [19].
The source term of pair production, s(p, t), obviously depends on the applied external field as well as the electron/positron kinetic property. From 
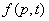
 | (2) |
Moreover when the integral part is represented by g(p, t) in Eq. (2), the equation can be expressed as a set of first order ordinary differential equations (ODEs)[16]
 | (3) |
 | (6) |
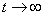
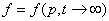
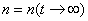
We use the electrons quantities as the normalized ones, i.e., the length 

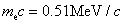
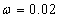


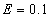

In this section, we will analyze the effect of the frequency chirp parameter on the pair production rate by discussing the laser pulse field, momentum spectrum and the number density.
The one-color laser pulse field is given by
 | (8) |
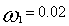

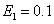
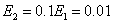
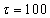
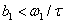
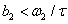
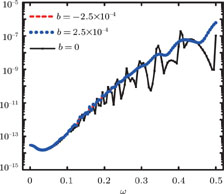
For some typical frequency chirp parameters b1 and b2 the momentum spectrum are depicted in
Fig.
 | Fig. 4. (color online) The same as in Fig.  |
In the case of the two-color laser pulse, first we study the effect of frequency chirping with the same signs of b1 and b2. The momentum spectrum curve is depicted in Fig. 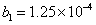
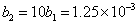



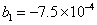

Second let us examine the effect of frequency chirping with the opposite signs of b1 and b2 when 

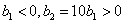


When 




 | Fig. 5. (color online) Electron–positron number density versus the ratio of magnitude of frequency chirp to the original frequency, where 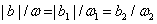  |
Now we will investigate which laser pulse chirping field contributes more to the pair production rate when 

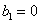

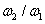


 | Fig. 6. (color online) Electron–positron number density vs the original two-frequency ratio in two-color pulse laser field 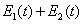 |
Finally, we keep 
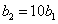








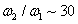
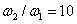
If we choose the number density curve of chirp-free, 






By solving the quantum Vlasov equation, we investigated the effect of frequency chirping parameter on the electron–positron pair production in one- and two-color laser pulse fields. The main findings of the present study are listed in the following.
(i) A positive or negative frequency chirp parameter is added to the one-or two-color pulse field, then the momentum spectrum and the number density curve of the created pairs in this field is obtained. It is found that in either one- or two-color laser pulse field the small frequency chirp shifts the momentum spectrum along the momentum axis, especially for the positive chirping. It can expand the detection probability by spectrometer.
(ii) Adding frequency chirp to the one-color pulse field results in a smoothing number density curve and the widening of the peaks in the multiphoton pair production process. The positive and negative frequency chirp parameters play the same role in increasing the number density. It is a natural result of time-reverse symmetry.
(iii) The sign change of frequency chirp parameter at the moment 
(iv) In the two-color pulse field, the number density is much higher than that in the one-color pulse field. The larger frequency chirped pulse field contributes more to increasing the pair production rate.
(v) In the two-color pulse field, the relation between the frequency ratio of two colors and the number density is not sensitive to the parameters of small frequency chirp added in either a low frequency field or a high frequency field but sensitive to the parameters of large frequency chirp added in a high frequency field.
(vi) When the frequency chirp parameter increases 6 times, the number density can increase 10 orders of magnitude. As the original frequency ratio becomes larger the number density curve presents a small oscillation behavior.
We believe that the results obtained here are helpful to deepening the understanding of the pair production by including the effect of frequency chirping, and in an alternative way one can expect to control the pair production through the appropriate frequency chirping.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] |