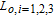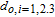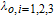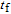† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 11404404).
A nonlinear controller for disturbances rejection and collision avoidance is proposed for spacecraft formation flying. The formation flying is described by a nonlinear model with the J2 perturbation and atmospheric drag. Based on the theory of the state-dependent Riccati equation (SDRE), a finite time nonlinear control law is developed for the nonlinear dynamics involved in formation flying. Then, a compensative internal mode (IM) control law is added to eliminate disturbances. These two control laws compose a finite time nonlinear tracking controller with disturbances rejection. Moreover, taking safety requirements into account, the repulsive control law is incorporated in the composite controller to perform collision avoidance manoeuvres. A numerical simulation is presented to demonstrate the effectiveness of the proposed method. Compared to the conventional control method, the proposed method provides better performance in the presence of the obstacles and external disturbances.
Spacecraft formation flying (SFF) is a concept that involves accomplishing space missions with multiple spacecrafts in designed arrays. SFF has many advantages over the traditional monolithic spacecraft system. It enables various space missions with enhanced reliability, flexibility, and efficiency. One notable mission involving the formation concept is the Defense Advanced Research Projects Agency's (DARPA) F6 program. This mission is to perform a common objective via distributed satellite operations. [1] SFF was developed as a revolutionary technique by NASA and ESA, used in the PRISMA mission, [2] TPF-I, [3] etc. Regardless of the broad prospects of SFF, technological challenges come with increased complexity, such as efficient fuel cost, precise formation control, and flying safety requirements. Efficient fuel cost is critical to any space mission, while high accuracy in control makes it possible to execute various space formation missions. Additionally, the collision avoidance problem is an important issue when formation reconfiguration is being carried out by multiple spacecraft manoeuvres in close range.
Many researchers have made significant contributions in the field of spacecraft formation control. The most popular model for formation flying is based on the Clohessy & Wiltshire (CW) [4] or Tschauner & Hempel (TH) [5] equation. Following this linear scheme, different methods have been proposed for formation flying. [6–8] To further improve the accuracy of control, investigations on nonlinear models and control strategies have begun in recent years. New nonlinear control techniques, such as sliding mode (SM), [9] recursive backstepping, [10] and nonlinear adaptive control [11, 12] have been investigated. During the last decade, the state-dependent Riccati equation (SDRE) has been a popular method for the design of controllers used in nonlinear systems. [13] It changes the nonlinear system to a pseudo-linear structure, which has state-dependent coefficient (SDC) matrices. Thus, the classical optimal control theory can be applied to the SDC matrices. This technique has been extended to spacecraft control. [14] For the tight formation reconfiguration, fast convergence is desirable. Compared to other finite time control methods, [15] SDRE could achieve finite time control and nonlinear optimal control simultaneously. An approximate closed-loop solution to optimally control spacecrafts with a finite time cost function was developed for the Reusable launch vehicle. [16] Therefore, the SDRE technique is an alternative method for nonlinear finite time optimal control.
For the spacecraft formation control, the state tracking accuracy should be guaranteed even in the presence of disturbances. An adaptive control architecture that rejects disturbances was proposed to solve the problem of tracking a manoeuvring target. [17] Using mean relative states, a nonlinear controller was derived for a pair of formation flying satellites, which includes the J 2 effect in system dynamics. [18] Based on second-order SM, a nonlinear controller was proposed for spacecraft formation flying in the presence of nonlinear dynamics and J 2 perturbations. [19] In the broad control area literature, an approach based on the Internal Mode (IM) principle has been developed to track the reference trajectory asymptotically and reject disturbances in uncertain nonlinear systems. [20, 21] Based on the IM principle, robust servo-regulators for uncertain satellite-systems were developed; these regulators were capable of eliminating the harmonic fluctuations caused by disturbance forces. [22] The IM principle has great advantages regarding disturbances rejection for formation tracking.
Flying safety requirements, such as path constraint requirements or collision avoidance, constitute an important and fundamental goal in spacecraft formation. Consequently, they have been actively studied by researchers in the control community. An analytical model of a predictive controller for fuel-minimised, collision-free trajectory has been cited in the literature. [23] Compared to other methods like semi-definite programming [24] or optimization-based methods, [25] artificial potential field (APF) guidance is considered an effective method to deal with safety issues. It has been used extensively in robot navigation and control [26, 27] and further extended to orbital vehicles. The autonomous on-orbit assembly of the large space structure has been presented using a superquadric APF. [28] By employing special potential functions and a time-varying sliding manifold, reference [29] studied target tracking, obstacle avoidance, and formation keeping. Based on potential functions and sliding manifolds, two control algorithms were proposed for formation flying with collision avoidance and disturbances rejection. A Riccati based tracking controller with collision avoidance has been presented for spacecraft formation flying near elliptic reference orbits. [30]
Nevertheless, only a few of the aforementioned works take the requirement of obstacle avoidance, finite time optimal control, and disturbances rejection into consideration simultaneously. Furthermore, the problem of finite time tracking with collision avoidance becomes more complex and difficult when designing control systems. Motivated by this open issue, formation flying, including the finite time approach, disturbances rejection, and collision avoidance, is to be considered in this work. The spacecraft proximity motion is described by nonlinear equations. Then, the SDRE method is adopted to solve the nonlinear control problem via SDC transforms. Because of its linear-like structure, IM is integrated to eliminate disturbances. Finally, the collision avoidance strategy is incorporated to form a composite control law. This composite controller is designed to achieve control objectives. As opposed to the work in [29], SDRE and IM are integrated instead of the SM, and the repulsive forces are defined in terms of two items. Reference [30] used the linear model, and disturbances were not considered; a different potential function was analysed. The major contributions of this study are summarised as follows: (i) the nonlinear model is converted into a pseudo-linear like form via SDC; (ii) the IM controller is integrated with the SDRE-based controller for finite time optimal control and disturbances rejection; (iii) flying safety is guaranteed by virtual repulsive forces in terms of both position and velocity.
The structure of this paper is as follows. Section
Consider multiple spacecrafts in Low Earth Orbit (LEO), where one of them is defined as the reference spacecraft, and the others are called followers. The relative dynamics of formation flying is described in the Local Vertical Local Horizontal (LVLH) frame. The LVLH frame is denoted by 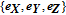
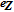
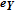
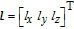
Let 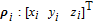
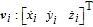
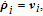 | (1) |
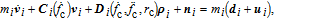 | (2) |
 |
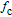
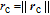
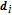
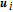
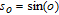
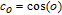
The rate of the true anomaly of the reference spacecraft is given by [32]
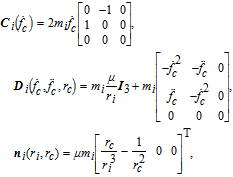 | (3) |
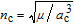
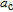
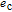
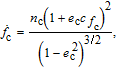 | (4) |
Disturbances are considered for a more precise relative dynamics. Some causes of external disturbances are the Earth's oblateness effect, atmospheric drag, and solar radiation pressure. For the spacecrafts in LEO (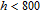
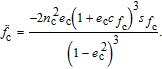 | (5) |
 |
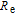
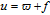
The relative effect of the atmospheric drag acting on the i-th spacecraft is obtained as [33]
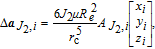 | (6) |
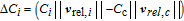
Thus, the total disturbance acceleration 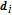
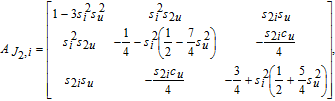 | (7) |
The control objective is to acquire a geometric formation configuration. The predetermined configuration considers each spacecraft in formation to be on one of the vertices of an equilateral triangle. Therefore, the reference spacecraft is also assumed to be on one vertex of the triangle. The goal is to design a closed-loop controller such that: (i) the other two spacecrafts reach the destination point at a specified time to form a triangular configuration; (ii) the disturbances are well rejected in the manoeuvring process as well as at the configuration point; (iii) no collision contact occurs when reconfiguration manoeuvres are executed.
The following assumptions are made for the synthesis of the control law. (i) The mass change in the i-th spacecraft is assumed to be small during the manoeuvre; thus m i could be assumed to be known and constant in the mission. (ii) Orbital elements of the spacecraft and the formation navigation information could be measured accurately and obtained in time. [35]
In this subsection, the SDRE principle and the SDC matrices are presented for nonlinear control. The nonlinear control law design is applied using the state space representation. The normal input-affine nonlinear system of the first-order differential state equation has the following form:
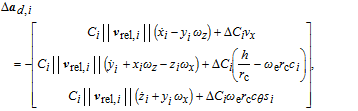 | (8) |
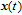

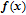
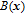
The finite time linear state-dependent quadratic cost function of the state and control vectors are defined as follows:
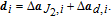 | (9) |
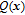
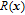
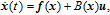 | (10) |
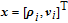
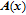
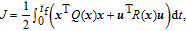 | (11) |
 |
The following assumption is made to obtain a closed loop solution using the SDRE method: [37] 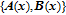
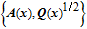

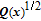
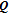
Then, the following equation is solved to obtain the optimal control input
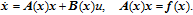 | (12) |
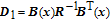
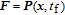
In the finite time case, the solution is a time-dependent differential equation rather than an algebraic one. For the position control of the formation, a finite time controller is designed based on the SDRE method. According to the finite time analytical approach, [38] the control acceleration is calculated as follows:
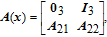 | (13) |
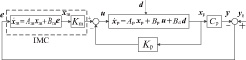
This subsection explains the process of designing a controller to reject the unknown disturbances and track the reconfiguration point. Figure
Generally, the disturbance consists of two parts: structure part and non-structure part. The structure part is the dynamic model of the disturbance, and the non-structure part is the magnitude gain. The system equation of the IMC is written as
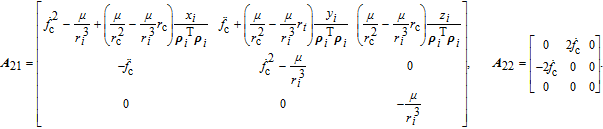 | (14) |
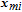
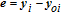
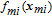
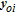
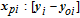
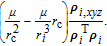 | (15) |
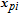
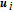
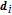
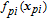
The original state can be extended to the components of a larger vector in an exogenous state. Defining the augmented state vector 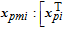
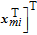
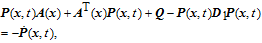 | (16) |
 |
The IMC gain and the state feedback gain are specified by 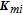
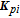
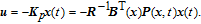 | (17) |
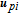
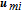
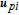
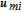
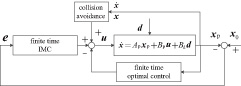
Collision avoidance during manoeuvres is achieved using high potential values to denote the forbidden areas. The vehicle could move away from the forbidden areas along the negative gradient of the APF. In space missions, the forbidden areas would be other space vehicles, path constraints, etc. To avoid a moving object, an intuitive scheme that takes into account the relative position and velocity components was designed by [41]. Owing to the symmetry of the Gaussian function and the spherical shape of obstacles, the proposed repulsive potential function is selected to be in a Gaussian form
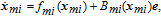 | (18) |
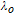
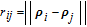
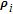
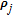
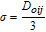
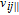
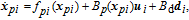 | (19) |
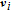
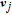
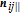
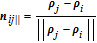
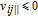
The influence region of the j-th spacecraft is defined as follows:
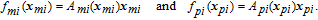 | (20) |
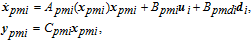 | (21) |
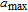
The perpendicular velocity between the i-th spacecraft and the j-th spacecraft is defined as
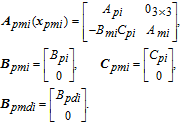 | (22) |
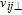
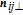
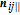
The corresponding repulsive force is defined as the negative gradient of the repulsive potential with respect to the position and velocity terms,
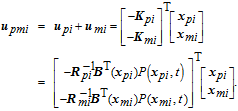 | (23) |
 |
The corresponding derivatives are computed as follows:
 |
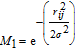
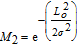
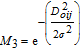
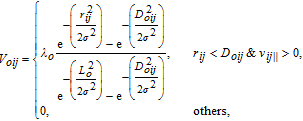 | (24) |
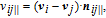 | (25) |
 |
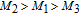
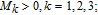
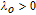
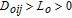
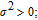
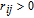
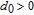
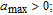
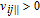
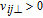
 |
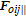
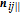
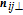
In this subsection, the process of designing a nonlinear feedback controller for achieving the control objectives is discussed. Given the relative motion described by Eq. (
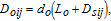 | (26) |
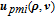
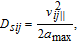 | (27) |
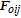
In this section, simulation results are presented for the formation flying control. As a demonstration of the proposed approach, a formation manoeuvre scenario is considered. In addition, two comparison scenarios are utilized to justify the performance. Table
| Table 1.
Physical parameters of the spacecraft. . |
| Table 2.
Parameters for the reference orbit. . |
| Table 3.
Symbols used in the simulations. . |
In this scenario, the desired triangle formation configuration has a 1000 m length on each edge. Table 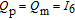
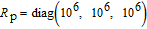
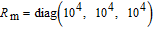
| Table 4.
Parameters used in the simulation. . |
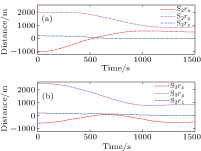
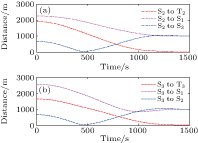
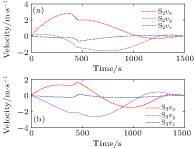
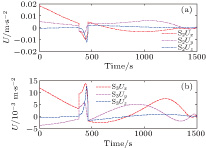
As shown in Fig.
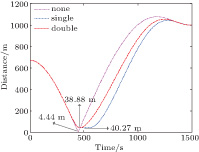
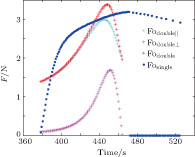
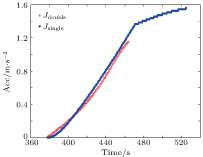
To validate the theoretical analysis, the controller with single repulsive force control [42] is verified and compared with the proposed controller in Eq. (
The relative distances between the spacecrafts are shown in Fig.
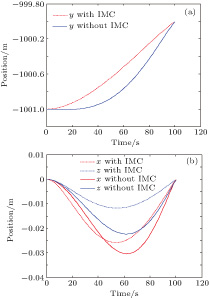
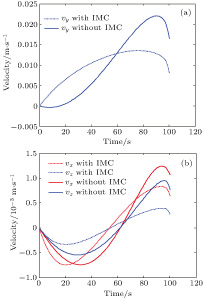
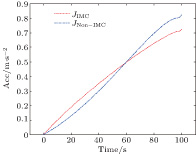
In this scenario, a comparison of IMC and non-IMC control strategies is made to show the effectiveness of the IMC controller. This scenario takes spacecraft S2 as an example. To evaluate the control method effectively, the comparison is made under an identical situation. The two spacecrafts have identical physical characteristics. The parameters of the orbit and spacecraft are given in Tables 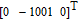
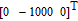
A composite control strategy has been proposed for spacecraft proximity operations. The design of the composite controller was divided into three parts. First, the dynamical model was converted into an approximately linear form via the SDC method, and the finite time suboptimal control law was designed based on the SDRE theory. Second, the IMC was integrated to reject the unknown disturbances. Finally, a composite control scheme was obtained by adding the APF control part. Forces in two different directions were generated to enhance the repulsive effect. The formation reconfiguration simulation was conducted to demonstrate the effectiveness of the proposed controller. Two additional comparisons were made to show the enhanced performance in collision avoidance and disturbance rejection.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 |