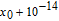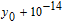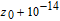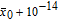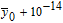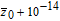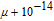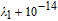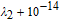† Corresponding author. E-mail:
In this paper, a novel image encryption algorithm is presented based on self-cited pixel summation. With the classical mechanism of permutation plus diffusion, a pixel summation of the plain image is employed to make a gravity influence on the pixel positions in the permutation stage. Then, for each pixel in every step of the diffusion stage, the pixel summation calculated from the permuted image is updated. The values from a chaotic sequence generated by an intertwining logistic map are selected by this summation. Consequently, the keystreams generated in both stages are dependent on both the plain image and the permuted image. Because of the sensitivity of the chaotic map to its initial conditions and the plain-image-dependent keystreams, any tiny change in the secret key or the plain image would lead to a significantly different cipher image. As a result, the proposed encryption algorithm is immune to the known plaintext attack (KPA) and the chosen plaintext attack (CPA). Moreover, experimental simulations and security analyses show that the proposed permutation-diffusion encryption scheme can achieve a satisfactory level of security.
Image is one kind of multimedia that has become increasingly important for communication in our daily life. It has many applications in different fields, for example, medical science, remote sensing, military, and traffic management. With the rapid development of Internet and wireless communication networks, where they are openly accessible, the protection of private images against intruders deserves much more attention than before. Traditional encryption algorithms such as AES (Advanced Encryption Standard), DES (Data Encryption Standard), and IDEA (International Data Encryption Algorithm) have been found to be unsuitable for image encryption [1–4] due to some intrinsic properties of images such as bulky data format, strong correlation between adjacent pixels, and high redundancy. Currently, a lot of image encryption algorithms [5–11] have been proposed to meet the challenge of security and efficiency requirements. Among these, many excellent features have been proved by chaotic maps, [12, 13] for example ergodicity, unpredictability, nonlinearity, pseudo-randomness, and sensitivity to both system parameters and initial conditions, which provide better performance and act close to confusion and diffusion in cryptography. [14, 15]
Recently, many new chaotic image encryption algorithms have been studied. [14, 16, 17] The architecture of permutation plus diffusion is the preferred model for designing chaos-based image encryption algorithms. On the one hand, permutation is used to exchange the pixel positions by a one-to-one mapping. As a result, the high correlation existing between adjacent pixels of the plain image can be greatly reduced. On the other hand, to alter the distribution of the gray values in the cipher image, diffusion operation is taken further to distribute all pixels. Sequentially, any tiny change (even just one bit) in a pixel will spread out to the other pixels and lead to a completely different output. A new hyperchaotic 2D map [18] was built from serpentine curve equations, which was employed in image encryption using permutation and diffusion. Then, in order to save time in the encryption process and achieve real-time communication, a new image encryption algorithm with combined permutation and diffusion was proposed in Ref. [19], in which the operation is accelerated by reducing the scanning effort for pixels. Fouda et al. [20] presented an encryption scheme with a single-round iteration, where the time consumption can be reduced due to the avoidance of real number arithmetic operations.
Unfortunately, some image encryption algorithms based on chaos were found to be insecure. For example, a chaotic encryption algorithm was proposed for color image in Ref. [21], where, with a permutation for row and column, together with a diffusion function for 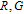
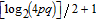
Based on cryptanalysis, the common security defects of the existing image encryption schemes are summarized as follows: (i) small key space, (ii) keystream generated independent of the plain image, (iii) a single-round iteration of the permutation plus diffusion structure. To solve these problems, an image encryption algorithm using self-cited summation is proposed in this paper. First of all, a three-dimensional intertwining logistic map is employed to enlarge the key space. Then, in both permutation and diffusion stages, the keystreams generated are dependent on the pixel summation of the plain image and the permuted image, respectively. Third, three rounds of iteration are adopted in the proposed algorithm. Then, detailed analysis will be performed to verify the security of the new design. The rest of this paper is organized as follows. Section
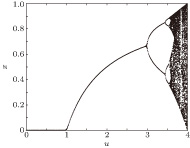
To generate chaotic sequences for permutation and diffusion operations, a nonlinear chaotic map or system is usually employed in a chaos-based image encryption algorithm. Because of the simplicity and low computation complexity, the logistic map [16, 28] has been widely used in recent years. It is defined by
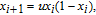 | (1) |
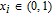
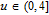
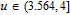
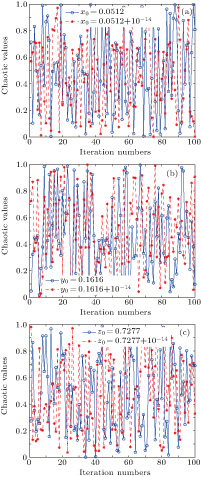
In order to solve the problems of the logistic map (
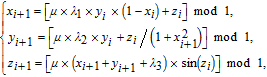 | (2) |
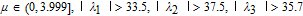
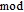
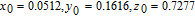
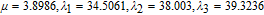
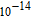
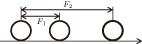
In physics, there is gravity between any two bodies in nature. The value of the gravity F can be calculated by
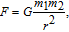 | (3) |
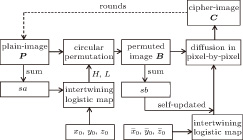
Suppose that the pre-encrypted gray image is A of size p × q. A color image can be divided into three channels R (red), G (green), and B (blue), each of which can be treated as a matrix corresponding to a gray-scale image. Because there exist some strong correlations between adjacent pixels in natural images, we try to decorrelate it to the ideal value (i.e., zero) in the new designed image encryption algorithm. Here, permutation of pixel positions is taken to implement the confusion effect. A good re-location effect should make the permuted image look like random noise.
To frustrate the common CPA and KPA (known plain attack), the keystream generated in the encryption process should be dependent on the plain image. It is noted that the permutation function is just to re-arrange the pixel positions but does not change the pixel values. That is, the pixel summation of the permuted image is equal to that of the plain image. Combining it with the gravity, we firstly compute the summation sa of the plain image and take it as the image quality (denoted as a body S) to influence itself in the permutation stage. For example, Figure 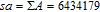
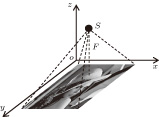
Since there is a distance between any two bodies to produce the gravity force, we assume that the plain image is put in the three-dimensional Cartesion coordinates, and the top–left corner of the image is located at coordinate (1,1,0). To simplify the ergodic permutation, each row (or each column) is treated as a unit in this new method. Pixel summation is treated as a body and is supposed to be put into the position of (1,1, (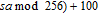
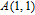
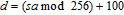
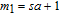
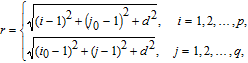 | (4) |
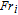
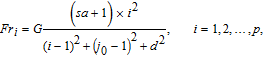 | (5) |
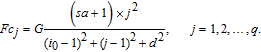 | (6) |
With initial conditions 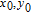
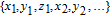
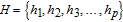
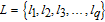
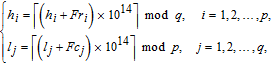 | (7) |
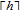
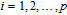
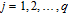
In order to resist statistical attack, the distribution of gray values in the cipher image should be different from that of the plain image. Usually, diffusion operation is taken after the permutation stage to spread the influence of any tiny change in the plain image to produce a significantly different cipher image. As we know, if the cipher image shows a fairly uniform distribution, then it can increase the difficulty for differential attack. Of course, the keystream generated dependence on the permuted image is very important for resisting KPA and CPA.
Firstly, all the pixels in B are arranged into a vector 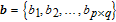
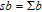
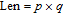
Assume that a chaotic sequence 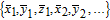
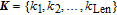
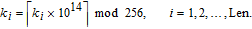 | (8) |
For each pixel in vector 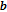
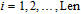
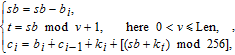 | (9) |
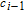
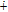
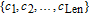
Note that the pixel summation of the plain image is used twice in the encryption processes, as can be seen from Eqs. (
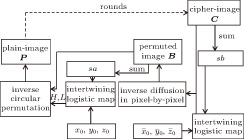
The architecture of the proposed image encryption algorithm is based on a permutation-diffusion mechanism. The encryption process is outlined in the following steps with encryption diagram and decryption diagram shown in Figs.
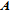
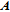
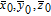
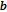
As we can observe from the above steps, the computation complexity of each step is equal to or smaller than 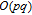
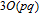
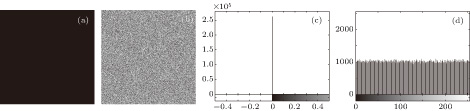
This section presents some experimental results of the proposed encryption algorithm. All the simulations are implemented by software Matlab R2011b on a platform of Windows 7 with Intel(R) Core(TM) i3-2350, 2.30 GHz CPU. Peppers of size 512 × 512, as depicted by Fig. 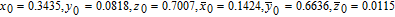
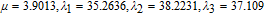
To resist the brute-force attack, the basic requirement for the key space is 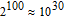
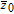
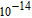
| Table 1
Comparison of key spaces. . |
A good image encryption algorithm should keep high sensitivity to every secret key to against CPA and linear cryptanalysis. [20] Here, the Peppers image is selected again to do the test. Figure 
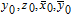
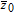
By the requirement of the avalanche effect for encryption schemes, any change in a pixel of the plain image, even just one-bit, should produce a totally different cipher image. To show the efficiency of our new algorithm, Figure
 | Fig. 9 Plain-image sensitivity test for Lena: (a) plain image, (b) first cipher image, (c) second cipher image, (d) difference between (b) and (c). |
Furthermore, NPCR (number of pixels change rate) and UACI (unified averaged changing intensity) are commonly taken to measure the influence of any tiny change in one pixel of the plain image on the cipher image, which are calculated by
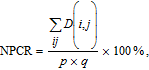 | (10) |
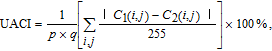 | (11) |
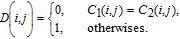 |
As to different images, the results of NPCR and UACI are listed in Table
| Table 2
Results of UACI and NPCR. . |
The image histogram shows the distribution of every pixel from 0 to 255 for a gray image. An efficient image encryption algorithm should make the histogram of the cipher image be fairly uniform and be significantly different from its corresponding plain image. To test the robustness against statistical attack, Figure
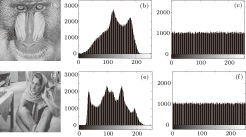 | Fig. 10 Histogram test for Baboon: (a) plain image, (b) histogram of plain image, (c) histogram of cipher image; Barb: (d) plain image, (e) histogram of plain image, (f) histogram of cipher image. |
For any natural image, high correlations can be found between pixels and their adjacent pixels. Usually, the following equation is calculated to get the correlation coefficients for both the plain image and its corresponding cipher image:
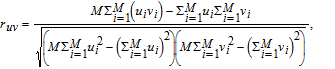 | (12) |
Here, Lena (see Fig.
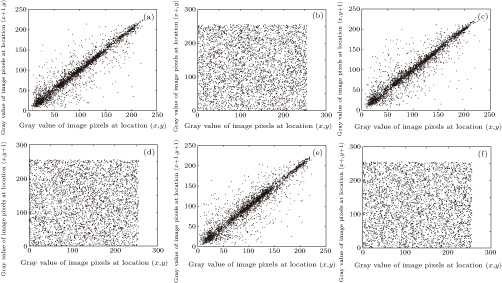 | Fig. 12 Correlation test for Lena image. Horizontally: (a) plain image, (b) cipher image; vertically: (c) plain image, (d) cipher image; diagonally: (e) plain image, (f) cipher image. |
| Table 3
Correlation coefficients for Lean image. . |
KPA and CPA are usually taken by cryptanalysts for security evaluation. [22, 26–30] In the proposed algorithm, pixel summation is considered in both permutation and diffusion stages. On the one hand, chaotic sequences H and L in Step 5 are generated to be dependent on the plain image for circular permutation. On the other hand, the keystream k
t
in Eq. (
In this section, to show the better performance of the proposed algorithm, some comparisons are given in Tables
| Table 4
Comparisons of UACI and NPCR. . |
| Table 5
Comparisons of speed for image size 512 × 512. . |
| Table 6
Comparisons of speed for image size 1024 × 1024. . |
A permutation-diffusion structure and self-cited pixel summation based image encryption algorithm have been presented in this paper. Image pixels are combined to produce the keystreams used in both permutation and diffusion operations. As a result, any tiny change in the secret keys or the plain image will lead to a significant alternation in the cipher image. Security analyses including key space, key sensitivity, plain-image sensitivity, histogram, correlation, KPA, and CPA demonstrate the high security and efficiency of the proposed encryption algorithm. Moreover, our method can be applied to any size of image in the gray level and can also be easily extended to color images with three components R, G, and B. Therefore, the new image encryption algorithm is suitable for real-time communications over public channels.
| [1] | |
| [2] | |
| [3] | |
| [4] | |
| [5] | |
| [6] | |
| [7] | |
| [8] | |
| [9] | |
| [10] | |
| [11] | |
| [12] | |
| [13] | |
| [14] | |
| [15] | |
| [16] | |
| [17] | |
| [18] | |
| [19] | |
| [20] | |
| [21] | |
| [22] | |
| [23] | |
| [24] | |
| [25] | |
| [26] | |
| [27] | |
| [28] | |
| [29] | |
| [30] | |
| [31] | |
| [32] | |
| [33] | |
| [34] |