In recent years, it was found that the complex network is ubiquitous in human society and nature and increasingly plays an important role in many fields, such as communication network, transportation network, and power grid, and so on.^[1–6] Therefore, the investigations about the dynamics behaviors of a complex network, especially about the network synchronization (including inner synchronization and outer synchronization), attract more and more comprehensive attention.^[7–11] For example, Huys et al. reported synchronization research of chaotic networks with multiple delays^[12] and Poria et al. discussed spatiotemporal synchronization of coupled Ricker maps over a complex network.^[13] Correspondingly, the various network synchronization methods have been proposed, for instance, projection synchronization, adaptive synchronization, sliding mode synchronization and backstepping synchronization method, etc.^[14,15]

The works about complex network synchronization reported previously focus mainly on the synchronization among all nodes within the network^[16–18] (so-called inner synchronization) and on the synchronization between two complex networks (so-called outer synchronization).^[19–22] In practice, however, the dynamics characteristics among some sub-networks connected to each other are also needed to analyze in-depth. For example, it is an urgent problem how to obtain the synchronization relationship among local networks or between local network and global network in the all optical communication network. Furthermore, the technique adopted for the synchronization of network group is different from these used in the synchronization within a network or between networks. Hence, the synchronization investigation about the network group which is constituted by a few sub-networks has become a hot topic in many research and application fields.

However, the research about synchronization of lots of complex networks, i.e., the so-called network group, has just started. A few works have been reported, for example, Jalan investigated the impact of the interaction of nodes in a layer of a multiplex network on the dynamical behavior and cluster synchronization of these nodes in the other layers.^[23] Singh studied the impact of multiplexing on the global phase synchronizability of different layers in the delayed coupled multiplex networks.^[24] Therefore, the research on the dynamics behaviors of the network group, especially on the synchronization principle, is still needed to explore in depth. In our work, a novel technique for realizing the synchronization among multiple networks is proposed and the controller forms of the nodes in every complex network are determined based on Lyapunov stability theorem.^[25] In order to demonstrate the effectiveness of our synchronization method, some Haken–Lorenz laser systems with chaos behaviors are selected as the nodes to construct a few nearest neighbor complex networks, at the same time, these sub-networks are also reconnected to form a network group. The complete synchronization among the sub-networks is realized perfectly under inner and outer couplings, which also indicates the work is of potential applications in the cooperation output of lasers and the communication network.

In this section, the synchronization mechanism of complex networks within the network group will be investigated. Some nonlinear dynamics systems with chaos behaviors are taken as the notes to construct M sub-networks (M = 3, 4, …) and to form a network group under inner and outer couplings. Within each sub-network, there are N nodes (N = 1, 2, …). Hence, the state equations of the i-th node in the 1st sub-network and the q-th sub-network can be respectively described as follows:

In this work, the first sub-network is set as target network and the rest of the sub-networks within the network group will track and synchronize with the first one. Under inner and outer couplings, the dynamics equations Eq. (2) of the corresponding nodes at respective controlled sub-networks are rewritten as follows:

Then, the derivatives of errors can be obtained

For the network group constituted by the complex sub-networks, we select the Lyapunov function as

Hence, we can gain:

Through choosing some appropriate node controllers in the q-th sub-network, the synchronization between the state variables belonging to different sub-networks q and p will be achieved while the conditions are satisfied.^[26] Therefore, we design the node controllers as

Substituting Eq. (9) into Eq. (8), then the latter can be rewritten as

Based on Lipschitz condition,^[14] that is, the following inequality will be satisfied while there exists a real number l_i > 0.

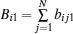
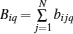
It can be found that the theoretic deduction in this section mainly focuses on a directed topology. In fact, this method can be applied in the synchronization of the network group with the bidirectional coupling as well. In this case, the state equations of the i-th nodes in the 1st sub-network and the q-th sub-network can be respectively rewritten as follows:

In our simulations, forty Haken–Lorenz laser chaotic systems with different initial values are taken as the nodes to construct four nearest neighbor networks and there are ten nodes in each sub-network. Haken–Lorenz laser system with chaos behavior can be expressed as follows:^[27]

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Evolutions of three state variables (a) and phase diagram (b) of the chaotic Haken–Lorenz laser.

Figure 2(a) is the topology structure of the nearest network with 10 nodes and figure 1(b) is diagrammatic sketch of the network group constituted by four sub-networks under inner and outer couplings. What needs to be explained is that four sub-networks are the same in our work for convenience, i.e., they are all nearest networks with 10 nodes, meaning the inner coupling coefficient matrices of four sub-networks are also the same and can be expressed as

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Topology structure of sub-network (a) and structure sketch of network group (b).

Figure 3 shows all error evolutions of ten nodes between target sub-network 1 and three controlled sub-networks with time, in which the meaning of can be understood as follows: d means the dimension (d = 1, 2, 3) of node state variable of the Haken–Lorenz laser; q represents the controlled sub-network (q = 2, 3, 4) and the second subscript 1 describes the target sub-network; i denotes node (i = 1–10) within every sub-network.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Error evolutions of ten nodes with time between (a) network 2 and network 1; (b) network 3 and network 1; (c) network 4 and network 1.

It can be found from Fig. 3 that the error curves will exhibit intense oscillations at the initial stage of evolutions, and tend to zero rapidly and keep zero after a transient oscillation (about 2.7 s) under the effective node controllers, even though the initial values of every Haken–Lorenz lasers at different nodes are diverse, indicating that the synchronization technique proposed in our work is effective.

Hence, it can be seen from Fig. 3, due to the imposed controllers in the controlled network nodes, all errors after transient oscillations all trend to zero quickly, which means that this section of the proposed synchronization scheme is effective.

In this paper, a new synchronization technique of inner and outer couplings is proposed in order to investigate the synchronization of the network group. The effective node controllers are designed based on Lyapunov function and the complete synchronization among the sub-networks is realized perfectly under inner and outer couplings. For validating the effectiveness of our synchronization method, forty Haken–Lorenz lasers with chaotic behaviors are taken as the nodes to construct four nearest neighbor complex networks and those sub-networks are also connected to form a network group. The simulation results show that all error evolutions between target 1st sub-network and the controlled sub-network tend rapidly to zero after a transient oscillation even though the initial values of all Haken–Lorenz lasers at every nodes are different, which means the synchronization technique proposed in our work is effective. This work is of potential application in the cooperation output of lasers and the communication network.