† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 61263019), the Program for International Science and Technology Cooperation Projects of Gansu Province, China (Grant No. 144WCGA166), and the Program for Longyuan Young Innovation Talents and the Doctoral Foundation of Lanzhou University of Technology, China.
In this paper, a standard susceptible-infected-recovered-susceptible(SIRS) epidemic model based on the Watts–Strogatz (WS) small-world network model and the Barabsi–Albert (BA) scale-free network model is established, and a new immunization scheme — “the most common friend first immunization” is proposed, in which the most common friend’s node is described as being the first immune on the second layer protection of complex networks. The propagation situations of three different immunization schemes — random immunization, high-risk immunization, and the most common friend first immunization are studied. At the same time, the dynamic behaviors are also studied on the WS small-world and the BA scale-free network. Moreover, the analytic and simulated results indicate that the immune effect of the most common friend first immunization is better than random immunization, but slightly worse than high-risk immunization. However, high-risk immunization still has some limitations. For example, it is difficult to accurately define who a direct neighbor in the life is. Compared with the traditional immunization strategies having some shortcomings, the most common friend first immunization is effective, and it is nicely consistent with the actual situation.
Recently, the complex networks have attracted attention of many researchers who are familiar with the field. The so-called complex networks are large-scale networks with complex topological structures and dynamic behaviors.[1] The complex networks are composed of a large number of nodes standing for individuals, and edges standing for interactions between individuals,[2] such as the internet, social network,[3] wireless communication network, the telecommunication network, friend relationship network, epidemic spreading network,[4,5] and other complex networks. With the rapid development of society, our daily life is closely related to the networks. Therefore, the studies of the structure, characteristics and relationships of networks have played a significant role in our daily life and scientific research.[6–8]
The earliest research of complex networks can be traced back to the problem of seven-bridges of Konigsberg in the eighteenth century. The random graph theory is the key of the complex network theory which was created by Erdos and Renyi in the 1960s. Now, complex networks have been studied widely. In recent years, an important branch of complex networks — the transmission mechanisms and propagation dynamics — has been widely investigated.[5,6,9] Throughout history, any epidemic’s outbreak is brought about by the social development of civilization. On the one hand, large-scale epidemics have a dramatic impact on the society. The network becomes an essential thing in our daily life, which promotes the continuous improvement of the modern health system and reduces the threat of epidemics. On the other hand, the increasingly developed social network makes the connection closer among people, which accelerates the great outbreaks of epidemics, such as SARS in 2003, H1N1 flu in 2005,[10] H7N9 in 2013,[11] HIV/AIDS,[12] and mad cow disease,[13] etc. These epidemics bring huge loss to the national economy and disaster to people’s lives.[14] Therefore, the presence of epidemics is a problem we have to solve.[15–17]
In 1959, two famous Hungarian mathematicians (Erdos and Renyi) created the ER random graph network model.[18] Like the regular networks, the ER random graph can be classified as homogeneous complex networks, in which the degree of each node in the network is approximately equal to the average degree of the network. By the 1990s, with the rapid development of the computer, internet and other technologies, the advents of various databases enables people to obtain a variety of topological structures of real networks. In this context, two landmark models, small-world network model[19,20] and scale-free network model[21] have been proposed. The characteristics of small-world networks show that the distance between any two nodes is much smaller than the network size, and similar to the six degree separation theory in sociology. The degree distribution is a power-law one on scale-free networks, in which exist some nodes of larger degree. The small-world and scale-free network models were two major statistical topological models at the end of the twentieth century.[22] Therefore, many problems are investigated on the two prototype complex networks.
Meanwhile, different propagation models are adopted in the various propagation behaviors. Classical propagation models were proposed by predecessors: susceptible-infected (SI),[23] susceptible-infected-susceptible(SIS),[24,25] susceptible-infected-recovered(SIR),[26] etc. Based on the above models, a lot of epidemic propagation models which are closer to the realistic ones are put forward, including susceptible-infected-recovered-susceptible(SIRS).[27] The transmission cases of three kinds of immunization schemes are studied by using the SIRS model.
Currently, with constant communications among people, more and more epidemics are spread to a wider range, which has brought huge influence to the human’s life and the economy. Therefore, designing a highly effective immunization strategy has been of wide concern.[28–33] Typical immunization strategies are as follows: random immunization,[34] targeted immunization,[35] acquaintance immunization,[36] and other immunization strategies.[37,38] Random immunization is a simple strategy, which completely randomly selects a part of nodes over the whole network, and carries out immunization, but it is almost immunization of all the nodes to obtain a better immune effect. So, random immunization is not impractical. Targeted immunization is an effective strategy, which chooses a small number of key nodes to immunize first. However, the only drawback is that it needs to know the topology of the entire network. Acquaintance immunization is to vaccinate random acquaintances of random nodes. It is obvious that the nodes with larger degree are easier to select. Other immunization strategies contain the double acquaintance immunization,[39] the complex vaccination adoption mechanism,[38] etc. Since these classic immunization strategies have some drawbacks, the latest immunization strategies are presented, respectively, with high-risk immunization[40] and the two-step high-risk immunization.[41] High-risk immunization is an effective strategy, which treats direct susceptible neighbors with infected nodes as high-risk groups, and controls the spread of epidemics by immunizing high-risk groups. The two-step high-risk immunization is designed, which immunizes not only partial high-risk nodes, but also partial indirect neighbors of infected nodes. In this paper, a new immune strategy — the most common friend first immunization — based on the topology research of complex networks, is proposed. High-risk immunization must know all susceptible individuals whose neighbors have been infected, and these individuals are called “high-risk individuals” or “direct neighbors”. In this paper, the most common friend first immunization only needs to know some direct neighbors and its neighbors. In real life, it is difficult to define all direct neighbors accurately, but it is very easy to find some direct neighbors and their neighbors. It is evident that the proposed method is more feasible than the high-risk immunization. Therefore, the most common friend first immunization is more operational, and is more suitable in real life.
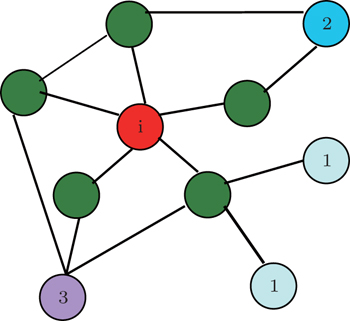
The idea of the most common friend first immunization is described in Fig.
The rest of this article is organized as follows. In Section 2, the most common friend first immunization on WS small-world network is introduced. In Section 3, the most common friend first immunization on BA scale-free network is described. In Section 4, the results and discussion of computer simulation on WS small-world network are presented. In Section 5, the results and discussion of computer simulation on BA scale-free network are given. Finally, according to the theoretical and simulation results, we can draw corresponding conclusions.
In 1998, Watts and Strogatz (WS) put forward the concept of small-world networks. Meanwhile, the WS small-world network model was also established, and it is constructed in the following steps: (i) starting from the rule graph: the starting point is a ring with N nodes symmetrically connected with its 2K nearest neighbors, (ii) random rewiring: for every node, each link connected to a clockwise neighbor is rewired to a randomly chosen node with probability p, and preserved with probability 1 − p.
In the SIRS model, each node represents an individual, and each edge represents direct contact between two individuals. The number of all edges connected to a node is defined as the degree of the node. Without considering isolated individuals, latent individuals, the birth and death rate of individuals in the propagation of epidemics, there are three node statuses, respectively, with susceptible status S(t), infected status I(t), and recovered status R(t). The infection mechanism of the classic SIRS model is showed in Fig.
The disease propagation process is described as follows. At each time step, a susceptible individual S is infected into an infected individual with probability β, an infected individual I is cured into a recovered individual with probability γ, while a recovered individual R becomes a susceptible individual, due to losing immunity, with probability σ. Therefore, the model’s effective transmission rate is λ = β/γ. In this paper, the probability with which any given node is a special node’s neighbor is defined as ω, and the probability per unit time in which one node obtains immunity by vaccinating is defined as o; At the same time, the proportion at which the direct neighbors of the most common friend are immune is defined as p, and the proportion at which the indirect neighbors are immune is defined as q. The degree distribution of homogeneous network (ER random graph network and WS small-world network) has a peak at the average degree 〈k〉, but the exponent declines when the value of k is significantly smaller than 〈k〉, and far more than 〈k〉. So, we suppose that each node degree ki is approximately equal to the average degree 〈k〉. Based on mean-field theory, when the network scale tends to infinity, the following dynamic equations can be obtained by ignoring the density correlation among different nodes:

Suppose that oij is the number of common friends between the infected node i and indirect node j, 


Here, S(t), I(t), and R(t), respectively, represent the average densities of susceptible individuals, infected individuals and recovered individuals. The first term on the right-hand side of the first equation denotes the average density of newly infected nodes generated by each infected node. The second term on the right-hand side of the first equation means the recovered nodes losing immunity with rate σ. The second term on the right-hand side of the second equation represents the infected nodes recovering with rate γ.
The most significant prediction of SIR is the presence of a nonzero epidemic threshold λc. If the value of λ is above λc, then the value of R(t) is above zero; it means that the infected individuals will spread infectious diseases, and the total number of infected individuals in the whole network is finally stabilized to a certain equilibrium state. If the value of λ is below λc, then the value of R(t) is equal to zero. It means that infectious diseases cannot spread, and the total number of infected individuals is infinitesimally small in the limit of very large populations. The S(t), I(t), and R(t) obey the normalization principle: S(t) + I(t) + R(t) = 1, the initial conditions of this equation are R(t) = 0, S(t) ≈ 1, and I(t) ≈ 0.
When the final infected density would reach a steady value, equation (

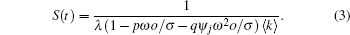



When σ = 0, the SIRS model is equivalent to the SIS model. Substituting σ = 1 into Eq. (

From Eq. (
Some phenomena of complex networks, especially of social networks, cannot be explained by WS small-world nor ER random graph network model. Because the degree distributions of the two network models obey the Poisson distribution, but the degree distributions of many networks in reality obey power-law distribution. For example, the transportation hub cities in China are limited in number, and these hub cities can reach many other cities, while the number of routes between the majority of common cities and other cities is relatively small. Another example is the case of the social network. In social networks, the public figures often have wide social circles and strong influence, while the social circles of ordinary people are relatively narrow and influence is relatively weak. To solve these problems, Barabasi and Albert proposed a scale-free network model based on the analysis of a large number of network data in 1999. The scale-free network model features a small number of hub nodes existing in the network. This model is proposed on the basis of two hypotheses: one is the growth pattern of the network: many networks grow, such as the production of new web pages in the internet, the addition of new friends in a friend’s net, etc; the other is the preferential attachment mode: as new nodes join, they tend to be connected with more nodes. For instance, the new web pages generally link to the well-known Web pages, etc. So, SIRS’ the most common friend first immunization epidemic model based on the scale-free network model is described as follows: constructing a BA scale-free network can lead to the growth and preferential connection. After enough iterations, we obtain a network composed of N nodes with degree distribution P(k) = k−3 and the average degree 〈k〉 = 2 m. According to mean-field theory, the dynamic equations of the BA scale-free network can be expressed as

In the BA scale-free network, the probability Θ(t) with which any given link points to an infected node can be expressed as

In the BA scale-free network, Sk (t), Ik (t), and Rk (t) obey the normalization principle: Sk (t) + Ik (t) + Rk (t) = 1. When there is no epidemic propagation in the network, dSk (t)/dt = 0, dIk (t)/dt = 0, dRk (t)/dt = 0, and Ik (t) = 0. Bringing this equation into Eq. (




From Eq. (



Substitute Eq. (









From Eq. (
From Eq. (
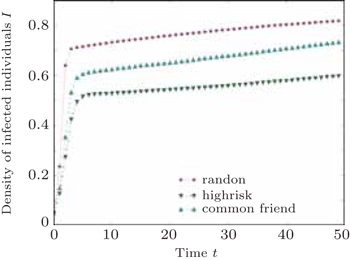
Based on the above analysis of mathematical theory, the corresponding experiments are also testified. Without loss of generality, a small-world network model is constructed: network scale N = 2000, the average degree 〈k〉 = 4, and the rewiring rate is 0.1. At the beginning, 5% of the susceptible nodes are infected. In each iteration, the susceptible node has the same probability with which it is infected by its neighbors. The prevalence is computed by averaging over 50 different starting configurations, performed on 20 different realizations of the network. Figure
Figure
Figure
Figure
From Eq. (
A scale-free network model is constructed with the following parameters: network size N = 2000 and the initial node size m = 5. At the beginning, 5% of the susceptible nodes are infected. In each iteration, the susceptible node has the same probability with which it is infected by its neighbors. The prevalence is computed by averaging over 50 different starting configurations, performed on 20 different realizations of the network. From Fig.
According to the theory of critical value of transmission, the transmission rate is larger than the critical value, and the infected individuals can spread. As described in Fig.
Figure
Figure
 | Fig. 9. Variations of density of infected individuals with infected rate for the most common friend first immunization on BA scale-free network, respectively, with N = 2000 and N = 3000. |
Figure
The adoption of appropriate immunization strategy is significant to prevent and control infectious diseases. In this paper, the most common friend first immunization scheme is proposed. According to the analysis above, the transmission cases of three immunization schemes based on small-world and scale-free network are simulated, respectively, with random immunization, high-risk immunization and the most common friend first immunization. The simulation results indicate that the immune effect of the most common friend first immunization is better than that of random immunization, but inferior to that of the high-risk immunization. The high-risk immunization must know all susceptible individuals whose neighbors have been infected. However, the most common friend first immunization only needs to know some direct neighbors and their neighbors. So, the most common friend first immunization is more feasible in reality.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 |