† Corresponding author. E-mail:
‡ Corresponding author. E-mail:
We report on the measurements of the electrical and dielectric properties of Na1/2La1/2Cu3Ti4O12 (NLCTO) ceramics prepared by high energy ball-milling and conventional sintering without any calcination steps. The x-ray powder diffraction analysis shows that pure perovskite-like CCTO phase is obtained after sintering at 1025 °C–1075 °C. Higher sintering temperatures result in multi-phase ceramics due to thermal decomposition. Scanning electron microscope observations reveal that the grain size is in a range of ∼3 μm–5μm for these ceramics. Impedance spectroscopy measurements performed in a wide frequency range (1 Hz–10 MHz) and at various temperatures (120 K–470 K) are used to study the dielectric and electrical properties of NLCTO ceramics. A good compromise between high ε′ (5.7 × 103 and 4.1 × 103 at 1.1 kHz and 96 kHz, respectively) and low tan δ (0.161 and 0.126 at 1.1 kHz and 96 kHz, respectively) is obtained for the ceramic sintered at 1050 °C. The observed high dielectric constant behavior is explained in terms of the internal barrier layer capacitance effect.
Since 2000, the giant dielectric constant (GDC) materials (ε′ > 103) have been extensively studied.[1–51] This is because of their potential applications in various electronic fields such as the charge storage capacitors.[9,10] These studies have resulted in the discovery of a large variety of GDC materials, mostly perovskite oxides, i.e., CuO,[11,12] [AC3](B4)O12 (where A = Ca, Cd, Sr, Na or Th; B = Ti; and C = Cu2+ or Mn3+),[1,13–19,29] (M, N)-doped NiO (where M = Li, Na, K, and N = Ti, Al, Si, Ta),[20,21] A(Fe1/2B1/2)O3 (where A = Ba, Sr, Ca and B = Nb, Ta, Sb),[22,23] and BaTi1–x(Ni1/2W1/2)xO3.[24] Nevertheless, CaCu3Ti4O12 (CCTO) is still the most studied material because of its special properties: room temperature dielectric constant value, ε′ of ∼ 103–104 that is independent of temperature and frequency over a wide range. Unfortunately, the loss tangent, tan δ of CCTO ceramics is still too large (> 0.05) which is an obstacle toward the application of CCTO to capacitor. Some new CCTO-related oxide ceramics are nowadays attracting the attention due to their low dielectric losses.[25–27] Low values of tan δ of 0.030–0.041 (1 kHz) and 0.022 (1 kHz) were reported for Na0.5Sm0.5Cu3Ti4O12[28] and La-doped Na0.5Bi0.5Cu3Ti4O12,[29] respectively. These results indicate that Na0.5Ln0.5Cu3Ti4O12 (Ln = La, Sm, Gd, Dy, Yb, and Y) ceramics may have a potential application to capacitor. Thongbai et al.[30] prepared Na0.5La0.5Cu3Ti4O12 by solid state reaction method in a process including two calcination steps (at 950 °C for 15 h and at 1000 °C for 10 h) followed by 5 h sintering at 1080 °C–1090 °C. The final ceramics showed an average grain size of 4 μm, ε′ ∼ 6.1–8.7 × 103 and tan δ ∼ 0.032–0.038 at 10 kHz. Liu et al.[31] prepared Na0.5La0.5Cu3Ti4O12 by sol–gel method including a sintering step at 1060 °C–1100 °C for 5 h–15 h. The ceramics sintered at 1080 °C for 10 h exhibited homogeneous microstructure with an average grain size of about 4 μm, ε′ of 1.1 × 104–1.8 × 104 and tan δ of 0.051–0.064 at 1 kHz–10 kHz which are about twice higher than the dielectric constant and loss tangent values reported by Thongbai et al.[30] This variation in the reported values of ε′ and tan δ for the same material reflects the dependence of the ceramics’ properties on the preparation method. In fact, the preparation method controls the microstructure, particularly the grain size and the electrical conductivity of the grain and grain boundaries which are determinant parameters for the dielectric properties of the GDC ceramics.[16,32,33]
In the present study we have prepared NLCTO by a simplified solid state reaction where the calcination step is dismissed. The powder of NLCTO is synthesized by high-energy ball milling technique. The dense and pure phase ceramics are obtained by conventional furnace sintering method. The influences of sintering temperature on the structural and dielectric properties of the prepared ceramics are also studied.
In this work, Na1/2La1/2Cu3Ti4O12 (NLCTO) powder was synthesized by mechanochemical milling of stoichiometric amounts of high-purity La2O3 (99.99%), TiO2 (99.9%), CuO (99.99%), and Na2CO3 (99.99%) in 2-propanol medium. The milling process was carried out by using Fritsch P-7 premium line machine for 30 h with a rotation speed of 500 rpm using a 45-ml tungsten carbide pot and tungsten carbide balls where the ball-to-powder mass ratio was 8:1. The resulting powder was then pressed into pellets each with 12 mm in diameter and 2 mm in thickness. Dense ceramics were obtained by sintering the pellets in air at 1025 °C, 1050 °C, 1075 °C, and 1100 °C for 10 h with a heating rate of 4 °C/min. The ceramics sintered at these temperatures are referred to as NLCTO-25, NLCTO-50, NLCTO-75, and NLCTO-00, respectively. The densities of the sintered pellets were calculated from their dimensions and weights. The prepared ceramic materials were characterized by field emission scanning electron microscope (FE-SEM) (Joel, SM7600F) technique. The x-ray diffraction (XRD) data were collected over the 0° ≤ 2θ ≤ 90° range using a Stoe Stadi-P Image Plate, IP, (Stoe and Cie GmbH, Darmstadt,Germany), with monochromated Cu Kα 1 radiation (λ = 1.5406 Å). The prepared ceramics have been crushed and ground into fine powder in an agate mortar before XRD measurements. Impedance spectroscopy (IS) measurements were performed by turnkey concept 50 system from Novocontrol over the 1 Hz–40 MHz frequency range. IS measurements were performed in dry nitrogen atmosphere in a 120 K–500 K temperature range, where the temperature was controlled by the Quatro Cryosystem. Silver paint was used as electrodes.
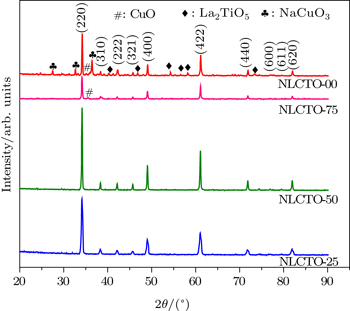
Figure
Figure
 | Fig. 2. FE-SEM morphologies of (a) the NLCTO powder and the fractured surface of NLCTO ceramics, (b) NLCTO-25, (c) NLCTO-50, (d) NLCTO-75, and (e) NLCTO-00. |
Figure
Figure
| Table 1. Elemental analyses of the grain and grain boundary regions for NLCTO ceramics. . |
 | Fig. 3. (a) EDX spectrum of the grain boundary for NLCTO-50 and (b) the EDX mapping of Cu from the surface of the NLCTO-75. |
Figure
The values of ε′ and tan δ at selected temperatures and frequencies for the studied NLCTO ceramics are given in Table
| Table 2. Values of ε′ and tan δ, measured at 310 K for NLCTO ceramics. . |
For more understanding of the dielectric relaxation in the current ceramics, we use the frequency dependence of the imaginary part of the electrical modulus M″ plots since this formalism identifies only the electrical responses with small capacitances. Thus, in the M″ spectra the electrode effects are usually suppressed. Figure
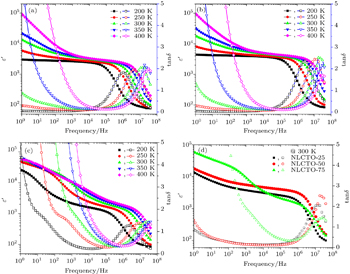 | Fig. 4. Frequency dependences of ε′ and tan δ for (a) NLCTO-25, (b) NLCTO-50, (c) NLCTO-75 at selected temperatures, and (d) all NLCTO ceramics at 300 K. |
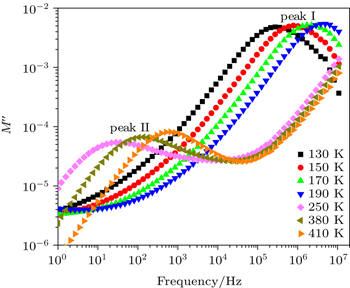 | Fig. 5. Frequency dependences of the imaginary part of electric modulus, M″ for NLCTO-50 at different temperatures. |
Since the frequency of M″ peak (fmax) is related to the mean value of the relaxation time (τ) as τ = 1/2π fmax, τ could be calculated at different temperatures. It has been found that the temperature dependence of the calculated values of τ follows the Arrhenius law:

| Table 3. Activation energy values, in unit eV, for conduction (ΔE) and for relaxation process (ER), and resistivity of grain (Rg) and grain boundary (Rg.b.) for NLCTO ceramics. . |
Giant dielectric values of CCTO ceramics are widely interpreted within the “brick work” model[43] which assumes the ceramic to be composed of semiconducting grains separated by insulating grain boundaries. Considering this model, the polarization effect at insulating grain boundary between semiconducting grains or other internal barriers is the main source for the giant value of dielectric constant. Therefore, it is important to study the electrical properties of the grain boundary and grain interior of the investigated ceramic. For this purpose, impedance spectroscopy was used to characterize and separate its electrical response. Figure
 | Fig. 6. Plots of logrithmic relaxation time τ versus 1000/T for NLCTO ceramics. Solid and empty symbols refer to the grains and grain boundaries, respectively. |
According to this model, the higher frequency semicircular arc of the impedance corresponds to the response of the grains, while the semicircular arc at low frequency corresponds to the response of the grain boundaries.[13] It is worth noting in the case that only a low-frequency semicircular arc exists, the resistivity of the grains can be determined from the non-zero intercept at the high-frequency limit.[45,46]
Figure
The frequency dependences of (−Z″) at selected temperatures for NLCTO-50 are given in Fig.
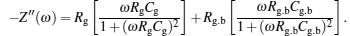

Figure

The obtained values of ΔEg (∼ 0.10 eV–0.129 eV) for the conduction in the grains in the present NLCTO ceramics are in good agreement with the values of ΔEg in the literature for CCTO and its related materials.[47–49] Nevertheless, ΔEg.b. is found to decrease considerably from 0.658 eV to 0.243 eV with sintering temperature increasing from 1025 °C to 1075 °C. The values of ΔEg.b. for the NLCTO-25 and NLCTO-50 lie in a range of 0.5 eV–0.7 eV that is widely found in the literature for CCTO-related materials.[45–47] It is worth noting that the value of ΔEg.b. for the NLCTO-75 is similar to the reported values of Bi2/3Cu3Ti4O12[50] and La3+ and Nb5+ co-doped CCTO[51] ceramics. The low value of ΔEg.b. for NLCTO-75 is likely to be related to the existence of intergranular CuO phase which has been approved by XRD and EDX analysis as discussed above. This result suggests the partial replacement of Cu2+ by La3+ in the grain boundaries, resulting in the increase of the grain boundary conductivity due to the higher density of free electrons. It is noticed from Table
Na1/2La1/2Cu3Ti4O12 (NLCTO) ceramics are successfully prepared by high-energy ball-milling and conventional sintering without any calcination steps. The phase formation analysis reveals that the ceramics sintered at 1025 °C–1075 °C consist of pure CCTO-like crystallographic structures. Sintering at 1100 °C results in thermal decomposition and subsequently the formation of a ceramic with multiphase structure. The present NLCTO ceramics have high values of ε′ in a range of ∼ 3.8 × 103–9.6 × 103 and 2.3 × 103–4.1 × 103 at 1.1 kHz and 96 kHz, respectively and tan δ of ∼ 0.161–2.075 and 0.126–0.440 at 1.1 kHz and 96 kHz, respectively. Complex impedance and complex electric modulus analysis reveal the electrically heterogeneous structure of the present NLCTO ceramic. Thus, the observed high dielectric constant behavior is explained in terms of the internal barrier layer capacitance effects.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 |