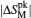
The magnetic refrigeration based on magnetocaloric effect (MCE) is superior to the conventional gas compression-expansion refrigeration technique due to its higher energy transfer efficiency and environmental friendliness.^[1–5] In recent years, the environmental degradation and the demand of new energy technique have aroused the passion of scientists to develop this advanced refrigeration technology and search for high-performance magnetocaloric materials, which exhibit large MCE, high refrigerant capacity (RC), and negligible hysteresis loss.^[6–9]

In the past few decades, large MCEs have been reported in many materials with magnetic transition from ferromagnetic (FM) to paramagnetic (PM) states, in which a negative magnetic entropy change ΔS_M (conventional MCE) is obtained by applying a magnetic field. On the other hand, the antiferromagnetic (AFM) material exhibits positive magnetic entropy change ΔS_M (inverse MCE) with applying a magnetic field due to the disordering of AFM sublattices antiparallel to the magnetic field.^[10,11] However, recently some AFM materials have also been found to exhibit large conventional MCEs, which are associated with the first-order field-induced metamagnetic transition from AFM to FM states.^[12,13] Moreover, the AFM–FM metamagnetic transition shows perfect magnetic reversibility, so it is favorable for the practical application in magnetic refrigeration. These results hint us that large reversible MCE could be found not only in FM materials but also in AFM materials.

As one of the important rare-earth (R) based series, the ternary intermetallic RTX compounds (R = rare earth, T = transitional metal, X = p-block metal) have been investigated systematically in the past decades.^[14–16] It is interesting to note that although the X atoms hardly contribute the magnetic moments, the crystallographic structure would vary with the change of X atoms, thus leading to the different magnetic and magnetocaloric properties of RTX compounds.^[16] For example, the HoNiSi compound crystallizes in the orthorhombic TiNiSi-type structure and experiences an AFM–PM transition,^[13] while the HoNiAl compound crystallizes in the hexagonal ZrNiAl-type structure and undergoes successive AFM–FM and FM–PM transitions.^[17] Moreover, the HoNiIn compound also crystallizes into ZrNiAl-type structure as HoNiAl, but it shows successive spin-reorientation-like transition and FM–PM transition.^[18] In order to further understand the effects of different p-block metals X on the magnetic and magnetocaloric properties in RTX compounds, in present work, we study the magnetic properties and MCE of HoNiGa compound in detail.

The polycrystalline HoNiGa compound was prepared by arc-melting appropriate proportion of constituent components with the purity better than 99.9 wt%. The ingot was flipped over and melted several times to ensure homogeneity. The as-cast sample was wrapped in tantalum foil and annealed in a high-vacuum quartz tube at 1223 K for 3 weeks, and then quenched in ice water. The crystal structure was investigated by powder x-ray diffraction (XRD) at room temperature through using Cu Kα radiation, and the structure parameters were determined by Rietveld refinement^[19] through using GSAS^[20]/EXPGUI softwares.^[21] The XRD investigation confirmed that HoNiGa compound crystallizes into a single phase with TiNiSi-type orthorhombic structure (space group Pnma). The lattice parameters obtained from Rietveld refinement as shown in Fig. 1 are a = 6.8161(3) Å, b = 4.2737(2) Å, and c = 7.3242(3) Å, respectively, which are in good agreement with the data reported in previous literature.^[22] The magnetic properties of the compound were measured by using a superconducting quantum interference device (model MPMS SQUID VSM) from Quantum Design, Inc.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Observed (dots) and calculated intensities (line drawn through the data points) of the fully refined x-ray diffraction pattern of HoNiGa compound at room temperature. The short vertical lines indicate the Bragg peak positions of the orthorhombic TiNiSi-type structure. The lower curve shows the difference between the observed and calculated intensities.

The temperature (T) dependences of zero-field-cooling (ZFC) and field-cooling (FC) magnetization (M) for HoNiGa compound under a magnetic field of 0.01 T are shown in Fig. 2(a). It is found that the HoNiGa compound undergoes a magnetic transition from AFM to PM states around the Ńeel temperature T_N = 10 K with the increase of temperature. In addition, it is worth noting that neither thermal hysteresis nor discrepancy between ZFC and FC curves can be observed, indicating the perfect thermomagnetic reversibility of magnetic transition, which is beneficial to the practical application of magnetic refrigeration. The temperature dependence of the reciprocal of magnetic susceptibility (χ⁻¹) under 1 T is also displayed in Fig. 2(a), and the relation between χ⁻¹ and temperature obeys the Curie–Weiss law in PM section. The paramagnetic Curie temperature (θ_p) and effective magnetic moment (μ_eff) of HoNiGa compound, determined by Curie–Weiss fit of χ⁻¹–T curve, are 13.3 K and 10.43 μ_B/Ho³⁺, respectively. This calculated μ_eff value is close to the theoretical magnetic moment of holmium cation (Ho³⁺: 10.60 μ_B), indicating that the magnetic moments of HoNiGa originate from Ho³⁺ while the Ni atoms hardly contribute the magnetic moments. This fact is consistent with many previous results about RTX compounds.^[13,23,24] In addition, as is well known, the θ_p value represents the sum of all magnetic interactions in system, and usually an AFM material exhibits a negative θ_p value.^[25] However, here the positive θ_p value indicates the presence of predominant FM interaction in HoNiGa compound under 1 T, so it suggests that the AFM ground state in HoNiGa is unstable and could be converted into an FM state by external magnetic field.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. (a) Temperature dependences of ZFC and FC magnetizations for HoNiGa under a magnetic field of 0.01 T and the inverse dc susceptibility (χ−1) as a function of temperature fitted to Curie–Weiss law in a magnetic field of 1 T; (b) temperature dependences of magnetization for HoNiGa under various magnetic fields.

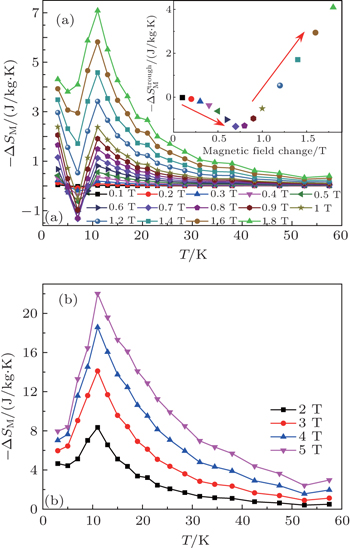
In order to further understand the effect of magnetic field on the phase transition, the temperature dependences of magnetization for HoNiGa compound under various applied fields are measured as shown in Fig. 2(b). The M–T curves at low magnetic fields each exhibit a typical λ-type peak around T_N, revealing that HoNiGa experiences an AFM–PM magnetic transition at low magnetic field. With the increase of magnetic field, the magnetization below T_N increases obviously, indicating the occurrence of the field-induced metamagnetic transition from AFM to FM states. When the magnetic field is larger than 0.8 T, the HoNiGa compound shows a step-like behavior of M–T curve, corresponding to the typical characteristic of FM–PM magnetic transition.^[26,27] Meanwhile, the magnetic transition becomes gentle with increasing magnetic field and the magnetization is still at high value in PM region under high magnetic fields. This fact implies the possible presence of field-induced short-range FM correlations in PM region.^[17,25]

Figure 3(a) shows the magnetization isotherms of HoNiGa compound under applied fields up to 5 T in a temperature range of 2 K– 8 K. It is seen from the inset of Fig. 3(a) that the magnetization under low magnetic field increases with the increase of temperature, revealing the characteristic of AFM ground state. With the increase of magnetic field, a sharp jump of magnetization occurs when the field reaches a critical value (e.g., 0.5 T at 2 K), which leads to a crossover of magnetization isotherms. Then, the magnetization decreases gradually with increasing temperature, corresponding to the characteristic of FM state. This result confirms that the AFM ground state in HoNiGa exhibits a weak stability and can be converted into FM state by applying an external field, which is consistent with the discussion of positive θ_p value. In addition, the saturation magnetic moment (μ_S), obtained by extrapolating the M–1/μ₀H curve to 1/μ₀H → 0 through using M–μ₀H curve at 2 K, is 9.56 μ_B/Ho³⁺, which is close to the theoretically calculated gJ value of 10.00 μ_B/Ho³⁺. This large μ_S value is attributed to the field-induced metamagnetic transition from AFM to FM states. On the other hand, it is seen from Fig. 3(b) that the magnetization changes remarkably around T_N = 10 K. Therefore, the high μ_S of field-induced FM phase and the large change of magnetization around the transition temperature imply the possibility of high MCE in HoNiGa compound.^[1,24] In addition, the magnetization isotherms at temperatures higher than T_N (up to 33 K) still show distinct curvatures as shown in Fig. 3(b), further confirming the presence of short-range FM correlations in PM region. As is well known, the magnetic hystereses in the magnetizing and demagnetizing processes will reduce the effective refrigerant capacity (RC) of magnetic material.^[28] Here, the M–μ₀H curves are measured in the field increasing and decreasing modes, and no magnetic hysteresis is observed. This perfect reversibility of magnetic transition is desirable for practical applications in magnetic refrigeration.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Magnetization isotherms of HoNiGa compound in the temperature regions of (a) 2 K–8 K and (b) 10 K–60 K, respectively. The inset of Fig. 3(a) shows the magnetization isotherms under relatively low magnetic fields. The Arrott plots of HoNiGa compound are in the temperature regions of (c) 2 K–8 K and (d) 10 K–18 K, respectively.

The Arrott plots are derived from the M–μ₀H curves and are presented in Figs. 3(c) and 3(d). According to Banerjee criterion, a magnetic transition is expected to be of first-order when the Arrott plot exhibits negative slope or inflection point; otherwise it is considered as second-order when the slope of Arrott plot is positive.^[29] It is seen that the Arrott plots below T_N show obvious negative slopes, confirming that the field-induced AFM–FM metamagnetic transition is of first-order. On the other hand, the positive slope of Arrott plot above T_N proves the characteristic of a second-order magnetic transition from PM state to FM state.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. (a) Temperature dependences of magnetic entropy change −ΔSM for HoNiGa compound under different magnetic field changes from 0.1 T to 1.8 T. The inset shows the −ΔSM through value below TN as a function of magnetic field change. (b) Temperature dependences of magnetic entropy change −ΔSM for HoNiGa compound under different magnetic field changes increasing from 2 T to 5 T.

The ΔS_M values for different magnetic field changes are calculated from magnetization isotherms by using Maxwell relation:

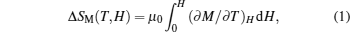
With the further increase of magnetic field, a large positive −ΔS_M peak (normal MCE) of −22.0 J/kg K can be found around the transition temperature for a field change of 5 T (Fig. 4(b)). This giant MCE is related to the high saturation magnetic moment of field-induced FM phase and the rapid change of magnetization around the transition temperature.^[24] Meanwhile, it is interesting to note that the −ΔS_M peak broadens asymmetrically towards higher temperatures with increasing field, which is likely to be related to the presence of field-induced FM correlation in PM region.^[31] As another important parameter to quantify the heat transferred from hot to cold sinks during an ideal refrigeration cycle, the RC value is estimated from the following formula:

Table 1.

Table 1.

Table 1. Magnetocaloric properties of HoNiGa and some other magnetocaloric materials with similar transition temperatures. . Materials TC/TN/K −ΔSMmax/(J/kg·K) RC/(J/kg) (5 T) Refs. 2 T 5 T TbCuSi 11 2.7 10.0 246 [32] Eu8Ga16Ge30 13 4.5 – 400 [33] Dy0.9Tm0.1Ni2B2C 9.2 4.05 14.7 220a [34] ErNi5 9 – 15.0 232a [35] ErNiIn 9 10.1 15.1 229 [18] DyNi2B2C 10.5 4.4 17.6 186a [36] HoCoAl 10 12.5 21.5 437a [37] HoCuAl 11.2 17.5 30.6 486 [38] DyCuSi 10 10.5 24.0 381 [39] HoNiGa 10 8.4 22.0 279 This work a The RC values are estimated from the temperature dependence of ΔSM in the literature.

Table 1. Magnetocaloric properties of HoNiGa and some other magnetocaloric materials with similar transition temperatures. .

According to the mean-field approximation, despite the diversities in the shape of −ΔS_M–T curve for different materials, the field dependences of −ΔS_M for all the materials with second-order magnetic transition can be expressed as

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. The value as a function of μ0H2/3 and the linear fitting to it.

In summary, the HoNiGa compound undergoes an AFM–PM magnetic transition under low magnetic field in the vicinity of T_N = 10 K. However, the AFM ground state can be converted into FM state due to its weak stability, and thus the HoNiGa undergoes a second-order FM–PM magnetic transition under high magnetic field. Moreover, perfect thermal and magnetic reversibility are observed in HoNiGa, and it is desirable for the practical applications in magnetic refrigeration. The field-induced FM phase exhibits a high saturation magnetic moment and a large change of magnetization around the transition temperature, thus leading to a large MCE. Besides, the field dependence of for HoNiGa can be expressed well by mean-field approximation, and thus it confirms the nature of second-order FM–PM magnetic transition under high magnetic field. Consequently, the large MCE without thermal and magnetic hysteresis makes HoNiGa compound a promising candidate for magnetic refrigeration materials in low temperature range.