† Corresponding author. E-mail:
Project supported by the Special Funds of the National Natural Science Foundation of China (Grant Nos. 11547226 and 11547180).
Cd1−xZnxS/Cu2ZnSnS4 (CZTS)-based thin film solar cells usually use CdS as a buffer layer, but due to its smaller band gap (2.4 eV), CdS film has been replaced with higher band gap materials. The cadmium zinc sulfide (CdZnS) ternary compound has a higher band gap than other compounds, which leads to a decrease in window absorption loss. In this paper, the band offsets at Cd1−xZnxS/Cu2ZnSnS4 (CZTS) heterointerface are calculated by the first-principles, density-functional and pseudopotential method. The band offsets at Cd1−xZnxS/CZTS heterointerface are tuned by controlling the composition of Zn in Cd1−xZnxS alloy, the calculated valence band offsets are small, which is consistent with the common-anion rule. The favorable heterointerface of type-I with a moderate barrier height (< 0.3 eV) can be obtained by controlling the composition of Zn in Cd1−xZnxS alloy between 0.25 and 0.375.
Cu2ZnSnS4 (CZTS) solar cell material has an ideal band gap (Eg = 1.5 eV) and high absorption coefficient.[1,2] As a possible alternative to the commercially available Cu(In, Ga)Se2 (CIGS), CZTS does not contain indium or gallium. Therefore, it could be a cheaper and more sustainable solar cell material in the future. Recently, a conversion efficiency of 12.6% for selenium containing CZTS[3] has been reported. However more research is needed to understand what prevents the devices from reaching as high efficiency as that of CIGS, which has record efficiency over 20%.[4] As is well known, CZTS-based thin film solar cells usually employ CdS as a buffer layer. However, the development of CdS/CZTS thin film solar cells is restrained by its smaller band gap (2.4 eV). One of the reasons is an unfavorable alignment of the conduction band minimum (CBM) at the CdS/CZTS heterointerface, where CBM of CdS is lower than that of CZTS.[5] This interface leads to an increase in interface recombination and a loss in open circuit voltage, Voc.
Cadmium zinc sulfide (CdZnS) ternary compound has a higher band gap, which leads to a decrease in window absorption loss and thus an increase in the short-circuit current. CdZnS is potentially useful as a window material for p–n junctions without lattice mismatch in the device based on quaternary material like CuInxGa1−xSe2 or CuIn(SzSe1−z)2.[6] ZnCdS has a variable band gap energy of 2.4 eV–3.7 eV, primarily dependent on a relative ratio of Cd to Zn.[7–10] The optimum conduction band alignment for CZTS should lie between the CdS and ZnS values. It has been reported that the pure CdS is expected to give a negative conduction band offset with CZTS,[11,12] and ZnS should cause the current to block due to a high barrier. Irvine et al. noted that the control of the alloying of ternary Cd1−xZnxS and keeping the thickness of the CdS window layer constant can cause the band gap to broaden.[13]
As is well known, the band offset at buffer-absorber interface is one of the most important parameters, which is often used to assess some important interface effects, i.e., quantum confinement and carrier transport, in particular, for the design of solar cells and other optoelectronic devices. There are numerous reports on the electrical and optical properties influenced by Zn substitution in CdZnS material.[14–18] The increasing of Zn composition in Cd1−xZnxS will enlarge the band gap, therefore, Cd1−xZnxS should lead to an increase of quantum efficiency (QE) in the shorter wavelength regime and also lead to favorable conduction band offset with CZTS. In this paper, we study the effects of Zn composition on the photovoltaic performance by calculating the band offsets for CdZnS/CZTS heterointerface with different Zn compositions. By changing the constituents of Cd1−xZnxS, the moderate barrier height at the Cd1−xZnxS/CZTS heterointerface is obtained.
Alloying is a good approach to performing band-gap engineering to extend the available band gap. In bulk Cd1−xZnxS alloyed crystal, its composition (x)-dependent band gap energy Eg(x) can be expressed by Vegard’s law[19]

The calculation of density of states (DOS) was performed on the basis of the first-principles, density-functional and pseudopotential method by using the PHASE code developed by Institute of Industrial Science, University Tokyo.[21] We used the generalized gradient approximation (GGA) for the exchange-correlation interaction,[22] with valence electron configurations of S (3s2, 3p4), Cu (3d10, 4s1), Zn (3d10, 4s2), Cd (4d10, 5s2) and Sn (4d10, 5s2, 5p2). For a given atomic arrangement, the lattice constants and atom positions were optimized to minimize the total energy.
We first obtained the energy level difference between the reference core levels (take the S 3s, Zn 3d, Cd 4d, and Sn 4d as reference core levels in the pseudopotential calculation method) and valence band maximum (VBM), from the band structures of Cd1−xZnxS and CZTS. Then, the core level difference was obtained from the band structure of the (001) Cd1−xZnxS/CZTS superlattice. The valence band offset EVBM and conduction band offset ECBM were obtained as[23,24]


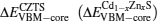
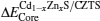
The total density of states for zinc-blend structures of ZnS and CdS are calculated as shown in Fig.
The band offsets at Cd1−xZnxS/CZTS heterointerfaces are tuned by controlling the Zn composition (x) in Cd1−xZnxS (x = 0, 0.125, 0.25, 0.375, 0.5, 0.75, 1) alloy. Since the band gap is generally underestimated in the calculation based on GGA, the band gap energy of Cd1−xZnxS as a function of Zn composition (x) is determined using Eq. (
| Table 1. Calculated band offsets at Cd1−xZnxS/CZTS heterointerfaces with different values of Zn composition (x) in Cd1−xZnxS (x = 0, 0.125, 0.25, 0.375, 0.5, 0.75, 1). . |
Figure
In the present paper, we calculated the band offsets at Cd1−xZnxS/CZTS heterointerface for different values of x, based on the first-principles, density-functional, and pseudopotential method. The band offsets at Cd1−xZnxS/CZTS heterointerface are tuned by controlling the composition content of Zn in Cd1−xZnxS alloy. Cd1−xZnxS/CZTS is a type I of heterointerface with a moderate barrier height smaller than 0.3 eV, when the composition content of Zn in Cd1−xZnxS alloy is between 0.25 and 0.375.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 |




