† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11272050, 11202090, 11472124, 11572034, and 11572145), the Science and Technology Research Project of Liaoning Province, China (Grant No. L2013005), China Postdoctoral Science Foundation (Grant No. 2014M560203), and the Doctor Start-up Fund in Liaoning Province of China (Grant No. 20141050).
It is a difficult problem to study the stability of the rheonomic and nonholonomic mechanical systems. Especially it is difficult to construct the Lyapunov function directly from the differential equation. But the gradient system is exactly suitable to study the stability of a dynamical system with the aid of the Lyapunov function. The stability of the solution for a simple rheonomic nonholonomic constrained system is studied in this paper. Firstly, the differential equations of motion of the system are established. Secondly, a problem in which the generalized forces are exerted on the system such that the solution is stable is proposed. Finally, the stable solutions of the rheonomic nonholonomic system can be constructed by using the gradient systems.
It is an important and difficult problem to study the stability for a nonholonomic constrained system.[1–17] It is also difficult to construct the Lyapunov function directly from the differential equations of the dynamical system. The authors in Ref. [18] pointed out that an ordinary differential equation can be written in a linear-gradient system when its one or more first integrations or Lyapunov function is given. In the past few years, some research advances have been made in the stability analysis for the nonholonomic constrained system, such as those given in Refs. [1]–[8]. But unfortunately most of the researches are limited to scleronomic nonholonomic constrained systems, because the stability analysis of the rheonomic nonholonomic constrained system is especially difficult and there has existed no general theory. In this paper the problem of stability analysis for a simple rheonomic nonholonomic constrained system is studied. The configuration of the simple dynamical system is determined by two generalized coordinates, which is subjected to a rheonomic unintegrable differential constraint in the sense of Frobenius theorem. The problem is what kind of generalized force should be used to be exerted on the system in order to make the system stable or aymptotically stable. In order to solve the problem, several kinds of gradient systems are utilized to construct the generalized force for the simple rheonomic nonholonomic constrained system. Recently, the important achievements for the relation between gradient system and constrained mechanical system have been made, such as those given in Refs. [19]–[22].
The configuration of a dynamical system is determined by two generalized coordinates, whose motion is subjected to a rheonomic nonholonomic differential constraint equation









The gradient system is suitable for discussing the stability of a dynamical system by utilizing the Lyapunov function. In this part, gradient system, skew-gradient system, gradient system with a symmetric negative matrix, generalized skew-gradient system and generalized gradient system with a symmetric negative matrix are used to construct the function F in Eq. (
The differential equations of a gradient system have the form







The differential equations of the skew-gradient system have the following form:






The differential equations of a gradient system with a symmetric negative matrix have the following form:

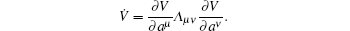
Let





Obviously, zero solution q1 = q̇1 = 0 of the rheonomic nonholonomic system is stable under the action of the generalized force Q1 of Eq. (
The differential equations of the generalized skew-gradient system have the following form:

Let




The differential equations of the generalized gradient system with a symmetric negative matrix have the following form:



Let






By using the Lyapunov function, the stability analysis of the nonholonomic constrained system is very difficult. However, the gradient system is exactly suitable to study the stability of a dynamical system with the aid of the Lyapunov function. In this paper, gradient systems are utilized to study the stability of a simple rheonomic nonholonomic system, where 3.1–3.3 and 3.4–3.5 are scleronomic and rheonomic, respectively. Some conclusions are given for the constructing generalized force.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 |


