† Corresponding author. E-mail:
Project supported by the Foundation of State Key Laboratory of Acoustics, Institute of Acoustics, Chinese Academy of Sciences (Grant No. SKLA201303) and the National Natural Science Foundation of China (Grant Nos. 11104044, 11234002, and 11474073).
Parabolic equation (PE) method is an efficient tool for modelling underwater sound propagation, particularly for problems involving range dependence. Since the PE method was first introduced into the field of underwater acoustics, it has been about 40 years, during which contributions to extending its capability has been continuously made. The most recent review paper surveyed the contributions made before 1999. In the period of 2000–2016, the development of PE method basically focuses on seismo-acoustic problems, three-dimensional problems, and realistic applications. In this paper, a review covering the contribution from 2000 to 2016 is given, and what should be done in future work is also discussed.
Since a one-way parabolic-equation (PE) approximation was introduced first by Tappert[1] to solve ocean sound propagation problems, some remarkable achievements have been obtained, particulary in recent years. Compared with most of other methods, the PE method is easy and fast in the speed of sound calculation in range-dependent problems, which expands its extensive development to the field of sound propagation in ocean acoustics. Some techniques are used to improve the computational accuracy and speed of PE models and make PE models more and more perfect.
Before the publication of this paper, there already have been several PE review papers.[2–9] Among these previous review papers the most recent one covered the development of PE made before 1999. In the present paper, a survey of contributions during the period from 2000 to 2016 is given.
The motivation for incorporating the elasticity of the sea bottom has made elastic PE models a hot topic. In comparison with traditional fluid PE models, an extra and important physical propagation mechanism that can be investigated in elastic PE models is the propagations of interface waves, namely Scholte wave, Rayleigh wave and Stoneley wave. Particularly, significant work has been done to handle the irregular interface between layers, which makes it possible to track the performance of interface waves in range-dependent environments. On the other hand, breakthroughs have been made in three-dimensional (3D) PE models, thanks to the developments of both PE theory and computer efficiency. The 3D PE models abandon the assumption of cylindrical symmetry, and thus are capable of solving a wider class of ocean acoustic problems. Efforts have also been made to apply PE method to various realistic problems, for example, forecast of reverberation. It should be noted that the authors may not be able to dig deeply into each of the subtopics covered in this paper. Therefore, readers should refer to the original literatures for more details.
To construct a clearer outline of the achievements in the past 16 years, throughout the entire context the contributions are basically allocated in three parts instead of being displayed according to published date. The first part reports general developments of PE method in theory, but is limited to the assumption of cylindrical symmetry, i.e., two-dimensional (2D) problems. The second part presents the contributions to 3D propagation modelling. The authors report this topic independently partly because 3D PE has been a very hot issue and will surely draw much more attention in future research. The third part gives some important applications of PE in solving realistic problems. Finally, some future needs are discussed. Figure
As is well known, the solutions of handling boundary conditions are very significant for the computational accuracy of parabolic equation models. There exist a lot of interfaces or boundary conditions in ocean waveguide, including the air-water interface, the fluid-fluid interface, the fluid-solid interface, the solid–solid interface and the infinity radiation boundary condition. Developments of treatments of boundary conditions generalize PE models to solve more complicated and extensive sound propagation problems.
First, new developments of handling sloping sea-bottom interface conditions are considered, containing single-scattering correction methods, variable rotated methods, coordinate mapping approaches and energy-conserving approximations.
In previous work, the single-scattering correction method was used to handle the sloping fluid-fluid interface[10] and the weakly sloping solid-solid interface,[11] which could obtain satisfying accuracies in PE models. In recent years, the method has been extended to deal with the sloping fluid-solid interface and the large contrasts across sloping solid-solid interface. In 2007, Küsel and Siegmann[12] described a single-scattering correction method which could handle large contrasts across interfaces and provide accurate solutions for a large class of seismic problems by working in the (ux,w) formulation. An iteration formula was used to solve the scattering problem which could improve convergence and obtain accurate solutions by using only one iteration. The formulation can be expressed as


There has been rotated parabolic equation approach[16] to solve the constant slope bottom sound propagation problems, after which Outing et al.[17] applied the approach to the problems with ocean bottom with variable slope and approximated a variable slope by using a series of constant slope regions. Moreover, they used an interpolation-extrapolation approach to generate a field starter at the beginning of each region beyond the one containing the source and used a series of operators to rotate the dependent variable vector along with the coordinate system for the case of elastic medium. Numerical simulations showed that the variable rotated parabolic equation could provide accurate solutions to a large class of range-dependent seismo-acoustics problems. After that, Collis et al.[18] applied variable rotated parabolic equation approach to sound propagation problems involving range-dependent bathymetry, variable thickness sediment layering, and variable topography, for studying range-dependent sound propagation problems along the beach and across the sea islands. When slope angle δ varied, a sound field phase correction was applied in the following formulation:

Moreover, they also developed an effective approach for dealing with water-sediment interface with low-shear speed. The precision of the computation results for the rotated parabolic equation was verified with the finite-element model.
In 2000, Collins and Dacol[19] first derived a coordinate mapping approach to deal with sloping interface in parabolic equation solutions, which took the form
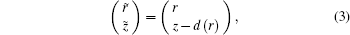
They applied a leading-order correction to the phase approximation to account for the effects of these terms. This mapping replaced a sloping interface with a sloping surface, because it was relatively easy to handle the case of a pressure-release boundary condition. In 2007, Sturm and Kampanis[20] analyzed the influence of “staircase” approximation on the one-way sound wave propagation problem. They presented a new finite-element 3D narrow-angle PE model which accurately treated the variable interface conditions by using an appropriate parabolized condition and a new change-of-variable technique which does not require any homotheticity condition of the layers. In 2014, Metzler et al.[21] derived a scaled mapping approach to PE models so that sloping bathymetry became horizontal for both surface and bottom interface. The scaled mapping formula they derived was
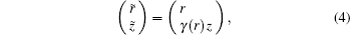
The fluid-sediment problem verified the validity of the new approach. The approach was universal for environments where bottom bathymetry varied with range.
The energy-conserving approximation of PE models is a very extensive technique to solve the range-dependent sound propagation problems. In previous work, the accuracies of sound propagation parameters have been improved by a higher-order energy-conserving PE both in fluid medium[22] and in elastic medium.[23] There are a lot of developments of the energy-conserving approximation to PE models in the 21st century. In 2000, Collins et al.[24] achieved an energy-conserving spectral solution. They approximated the range-dependent medium to a series of range-independent regions where sound field could be expressed as a term of the horizontal wave-number spectrum. An energy-conserving condition was used to handle the vertical interfaces between regions. Numerical simulations of sloping ocean sound propagation problems testified the accurate solutions of the energy-conserving spectral solution. It is obvious that energy conservation of a differential equation cannot prove to be energy conservation of a numerical solution of the equation, that is, energy conservation must be verified for discretized equation directly. In 2001, Mikhin[25] developed a numerical solution of a PE model OWWE presented by Godin[26] in 1999, which preserved energy conservation and reciprocity of the differential equation. Some components of OWWE were considered by using discretization method, such as the starting field, the boundary conditions and the finite difference operators. Some numerical results demonstrated discrete energy conservation and flow reversal theorem of the numerical model. Afterwards, Mikhin[27] derived an energy-flux PE model in the following expression:



The energy-flux PE can preserve energy conservation of the boundary condition at the vertical interface due to the continuity of energy-flux U. Compared with an earlier Padé PE model,[23] the energy-flux PE may increase accuracy of 1–2 decimal digits with the same steps. In 2007, J Z Liu and R Z Liu[28] applied the energy conservation method to the 3D PE model[29] to handle the bottom boundary conditions. Simulations of the ASA benchmark wedge problem proved to improve the accuracy of the new algorithm by using the principle of energy conservation.
Now we will introduce solutions of infinity radiation boundary conditions, including perfectly matched layer techniques and transparent boundary conditions.
The perfectly matched layer (PML) is an effective technique for truncating unbounded domains with minimal spurious reflections. It was primitively introduced by Berenger[30] to solve some electro–magnetic problems in time domain. Then, some discussion and improvements about time domain PML were implemented. PML was applied to the frequency domain when Ha et al.[31] studied Maxwell’s equations. As was followed, more studies and improvements in frequency domain PML were presented.[32–36] Lu and Zhu[37] applied frequency domain PML to a 2D fluid PE model to solve range-dependent benchmark problems, which built a foundation for this paper. A complex coordinate stretching originally introduced by Chew and Weedon, which is a key method in frequency domain PML technique, was used in Lu and Zhu’s implementation. It can truncate unbounded domains with minimal spurious reflections. Lu and Zhu modified the complex coordinate stretching in the following expression:

In 1998, Arnold and Ehrhardtc[39] presented the transparent boundary conditions (TBCs) for the 2D wide-angle PE models (WAPEs) in underwater acoustics. They derived a novel discrete TBC from the fully discretized whole-space problem which was reflection-free and yielded an unconditionally stable scheme. Then, Petrov and Ehrhardt[40,41] implemented the transparent boundary conditions (TBCs) for such systems of coupled parabolic equations and proved the existence and uniqueness of the solution of the initial boundary value problem for the system of iterative parabolic equations with the derived boundary conditions. Moreover, they proposed an unconditionally stable finite difference scheme for its solution.
Finally, a special technique called non-local boundary conditions to handle different boundary conditions is discussed.
Artificial absorption layers are usually used to truncate the infinity domain of PE models in underwater acoustics. An alternative method is the non-local boundary conditions (NLBCs) which can be used to handle a lot of interface conditions, such as an interface between two media, a general impedance boundary and the initial conditions. In 2000, Brooke and Thomson[42] applied NLBCs which were expressed by plane-wave reflection coefficients to the high-order Padé-based PE algorithms. Especially, the non-local boundary conditions were developed to account for the coherent losses due to scattering by a statistically-rough sea surface. In 2004, Mikhin[43] obtained NLBCs for high-order finite-difference parabolic equations by using Z transformation of the discrete PE in a homogeneous medium. A lot of NLBCs were derived which included the free-space radiation condition, possibly with a density jump at the NLBC interface, the NLBC at an arbitrary impedance interface, and the NLBCs for sources and the starting field beyond the NLBC interface. The obtained NLBCs were exact for the given finite-difference scheme and were not limited by the order of Padé approximation nor by the PE steps in range and depth. The accuracy and performance of the algorithm were analyzed for several benchmark problems. In 2005, the concept of optimal boundary control was applied by Meyer and Hermand[44] to solve inverse problems in shallow water acoustics. A generalized nonlocal impedance boundary condition at the water-bottom interface was used to derive a continuous analytic adjoint model for the Claerbout wide-angle parabolic equation. In 2008, Mikhin[45] developed the foregoing method[43] and presented the analytical inverse of the matrix composed of Padé partial fractions which led to closed-form analytic expressions for the elements of the Z-transformed NLBC matrix in the energy flux PE model. The analytic solution was also faster within the common domain of applicability. Papadakis and Flouri[46] modeled the acoustic propagation problem via the parabolic approximation. The computational domain was restricted to the water column, while the stratified bottom region was modeled by a nonlocal boundary condition. They developed non-local boundary conditions which were imposed on the actual water/bottom interface in a horizontal waveguide, or along a computational horizontal interface below the actual bottom, in the form of Neumann to Dirichlet (NtD) or Dirichlet to Neumann (DtN) maps. Some benchmark problems demonstrated the validity and performance of the new model.
The development of elastic PE method from 2000 to 2016 is mainly enhancing the capability of HEPE, which was proposed in 1989 by Collins.[47] The marching solution of this model is


In 2006, Collins et al.[49] discussed the possibility of handling multi-layered range-dependent problems by rotating the coordinates or single-scattering. Then, Outings et al.[50] applied the mapping approach to multi-layered range-dependent problems, i.e., using the mapping approach to handle both fluid-solid interface and solid-solid interface. The mapping solution was applied to a problem involving conversion of a Scholte wave to a Rayleigh wave in a beach environment. However, one has to keep in mind the limitation here, that is, all the interfaces involved in the elastic bottom need to be parallel to the fluid-solid interface. In 2010, Zhang Haigang et al.[51] studied the conversion of water-borne acoustic waves into Rayleigh waves on shore. In 2008, Collis et al.[52] proposed a modified elastic PE model, which handles fluid–solid interfaces with the coordinate rotated approach and handles solid–solid interfaces with the single-scattering approximation. A finite element solution was employed as the benchmark solution. Another mentionable work is the MEI-incorporated solution presented by Collis and Metzler[53] in 2014. MEI is an acronym for massive elastic interface. The purpose of this technique is to handle thin and low-shear speed ocean bottom sediments. The surface layer is approximated as a thick, finite-thickness interface, and modified ocean bottom fluid-solid interface conditions are derived as jump conditions across the interface. However, this technique is not applicable for every ocean bottom study, particularly those which involve interface waves or shear wave resonances, as propagation is not permitted through the interface and these phenomena are necessarily excluded.
In order to study energy conversion between elastic and acoustic waves, Frank et al.[54] in 2013 implemented two types of elastic parabolic equation self-starters, i.e., a compressional self-starter and a shear self-starter, for seismic sources located in elastic bottoms. On this basis, more simulations and analyses were presented in the work by Frank et al.[55] in 2015. Down slope conversion of elastic waves from seismic sources into T-waves trapped in the SOFAR channel, which is a key generation mechanism of oceanic T-waves, was clearly exhibited.
The modified HEPE was extended to handle problems involving ice cover and other thin elastic layers by Collins[56] in 2015. The key step to achieve this goal was said to be finding a proper rational approximation for the square root operator in the parabolic equations. A rational approximation that combines the rotated Padé approximation and the stability constraints was proposed in this literature. However, Collis et al.[57] in 2016 argued the above effort, indicating that in the construction a complex rational approximation might be unnecessary. In the work by Collis, the square root operator was merely approximated by an old version of Padé approximation[58] proposed in 1991. Their solutions were benchmarked against normal mode and wavenumber integration solutions. Plate flexural modes that propagate in the ice layer, as well as Scholte interface waves that propagate at the boundary between the water and the seafloor, were exhibited.
In 2000, Fredricks et al.[59] presented a parabolic equation for anisotropic elastic medium. The anisotropic wave equation was formulated in terms of a special set of variables to avoid third-order terms, facilitate factorization, and simplify the interface conditions. Metzler et al.[60] in 2013 extended the modified HEPE to layered poro-elastic medium. Two new variable formulations were presented.
When sound propagation problems which include broadband or high frequency signals, long-range or deep-water environment are considered, the program memory and the speed of sound field calculation could be a restraining factor for sound field computation. With the development of the multi-core computer, people sought for accelerated algorithms to enhance the efficiency of sound field computation. What followed was that parallelized algorithms and non-uniform grid algorithms were introduced.
In 2008, Castor and Sturm[61] developed a parallelized algorithm which is based on an existing 3D wide-angle parabolic equation model in a massively parallel computer. The algorithm is a two-level parallelization: the frequency decomposition and the spatial decomposition of the calculations. They tested the performance of the parallelized algorithm by using the example of the 3D extension of the classical ASA wedge benchmark. In 2009, Wang and Peng[62] realized a parallelized algorithm for the parabolic equation model RAM on the basis of the OpenMP. Testing results showed that the algorithm could obtain high computation efficiency. In 2011, OpenMP and MPI were used to parallelize the Range-dependent Acoustic Model (RAM) by Wang et al.[63] to accelerate the sound field computation. The implementation platform was built on a symmetrical multiprocessing cluster, which included multiple nodes and CPUs. Numerical results showed that the new parallelized algorithm had high parallel efficiency.
The pattern of grid partition for parabolic equation model can affect computational speed and precision of the model. Researchers have been promoting grid partition strategies unceasingly for improving both computational speed and precision simultaneously. In 2010, Austin and Chapman[64] implemented the concept of tessellation in the full 3D parabolic equation model (MONM3D) and incorporated techniques that reduced the required number of model grid points and reduced computation time. The tessellation allowed the number of radial paths in the model grid to vary with range from the source, which reduced the number of computational points in the horizontal plane. In 2013, Sanders and Collins[65] implemented a non-uniform depth grid method and modified a discretization of Galerkin method in PE models. They used Galerkin’s method with asymmetric hat functions to discrete the depth operator. Some simulations showed that the non-uniform grid algorithm could be used to improve the efficiency for the problems in ocean acoustics and seismo-acoustics.
The computational accuracy is almost the most significant factor of PE models, which is analyzed and improved by some contributions.
It is a very significant problem to estimate the accuracy of the parabolic equation models in underwater acoustics. In 2003, Larsson and Abrahamsson[66] developed an approach to solving the Helmholtz equation to estimate the errors in PE solutions. The new method applied a preconditioned Krylov subspace method that combined domain decomposition and fast transform techniques to the discretized equations. The method can generally indicate the magnitude of the error, whereas it was not a strict error bound.
In 2005, Flouri et al.[67] developed the high-order accurate methods for the numerical solution of the standard (narrow-angle) parabolic equation and considered many explicit and implicit numerical schemes. They found that the explicit schemes and some of the proposed high-order accurate implicit methods had stability limitations. To break these limitations, they developed an implicit finite-difference scheme which can meet an unconditional stability.
As is well known, the PE models usually use the far-field approximation to simplify the complicated equations which can bring additional error to the result of sound field. In 2006, Song and Peng[68] analyzed and modified the far-field approximation for RAM as well as the numerical calculation for PE starter. They developed a new propagator without the limitation from the far-field approximation. Numerical simulations of sound propagation problems in the Pekeris waveguide showed that more accurate calculation of PE self-starter and transmission loss can be obtained by using the new propagator.
Compared with other sound propagation methods, the PE method cannot obtain an accurate phase results of sound field computation. To eliminate phase errors, in 2006, Rypina et al.[69] applied the environmental transformation technique to the standard parabolic wave equation. The technique can eliminate PE phase errors for all propagation angles simultaneously in a range-independent environment. Although the transformation in range-dependent environments cannot be efficient, the transformation was expected to reduce PE phase errors to a negligibly small level when applied to a sequence of profiles in a slowly range-dependent environment.
Underwater acoustics is an experimental science, where the validities and performances of various models must be verified experimentally, so must the parabolic equation sound propagation models. The complicacy, uncertainty and uncontrollability of the real ocean environment make it difficult for models to be verified through sea-trials. To solve the problems, researchers try to conduct lab experiments under controllable environments to verify the validity of the parabolic equation models.
There are mainly two international tank experiments in relevant researches. In 2007, Collis et al.[70] carried out a tank sound propagation experiment and obtained high-quality experimental data. They simulated the elastic seafloor with a polyvinyl chloride slab which had high rigidity and could be used to consider the effects of shear waves on sound propagation and obtained acoustic measurements along virtual arrays in the water column by using a robotic apparatus. Numerical results of the elastic parabolic equation in flat and sloping configurations were in excellent agreement with the experimental data. Unlike the foregoing experiment, a series of experiments to create a waveguide with variable bottom slope with using two PVC slabs joined at an angle were conducted by Simpson et al.[71] in 2011. The experimental results demonstrated the validity of the elastic variable rotated parabolic equation in handling variable bottom slope.
Zhu et al.[72] in 2013 also carried a scaled tank experiment in an anechoic tank to verify the validity of the elastic parabolic equation approximation method for sound field calculations. It was shown that simulation results were in excellent agreement with the measured results, verifying the validity of the accuracy of the two parabolic equation methods.
It is clear that the real ocean is 3D and very complicated. When sound propagates in ocean waveguide, 3D effects of sound propagation such as horizontal refraction effects and sound field diffractions must be considered on various occasions where sound intensity can be coupled at different horizontal azimuth angles. The 2D models cannot meet the need of real 3D sound propagation problems, so 3D PE model is ready to come out. In recent years, there are many developments in modeling 3D fluid PE, including the first model For 3D presented by Lee et al.[29] in 1992. Then, people sought for improving square operator approximation and solutions of PEs and many 3D models are built to solve a lot of classical 3D sound propagation problems. Moreover, there are a lot of outstanding researches on analyses and capabilities of 3D PE models.
In 2001, Brooke et al.[73] presented a Canadian N×2D/3D PE underwater sound propagation model PECan which was developed for matched field processing applications. PECan based on standard square-root operator and/or propagator approximations that led to an alternating direction solution of the 3D problem featured a heterogeneous formulation of the differential operators on an offset vertical grid, energy conservation, a choice of initial field including self-starter, and both absorbing and nonlocal boundary conditions. The 3D azimuthal corrections were computed using either a split-step Fourier method or a Crank–Nicolson finite-difference approximation. Especially, losses due to shear wave conversion in an elastic bottom were handled in the context of a complex density approximation. The formulation of the complex density approximation can be written as

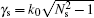
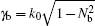
In 2003, Sturm and Fawcett[74] built a 3D PE model which used higher-order finite difference schemes to deal with the azimuthal derivative term and considered point source starting field of this model. The square-root operator was approximated as the following expression:
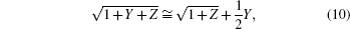
The numerical results showed that a higher-order scheme in azimuth can reduce the required number of points in the azimuthal direction but still obtain accurate solutions. Two years later, Sturm[75] proposed a time-domain and frequency-domain four-dimensional (4D) sound propagation model to investigate the propagation of a broadband sound pulse in 3D shallow water ocean waveguides. The Fourier synthesis technique and the fully 3D parabolic equation based model 3DWAPE were applied to the time-domain and frequency-domain calculations, respectively, and sound propagation simulations of the 3D ASA benchmark wedge and the 3D Gaussian canyon were described. In 2005, according to the generalized phase integral (WKBZ) theory and the Beam-Displacement Ray-Mode (BDRM) theory, Peng and Zhang[76] presented a 3D coupled mode PE model (CMPE3D) which was expressed in terms of the normal modes in vertical direction and the coupled mode coefficient in horizontal directions, which was solved by a PE-based algorithm. Numerical results indicated that the efficiency and accuracy can be improved by CMPE3D.
In 2012, Lin and Duda,[77] and Lin et al.[78] presented two 3D PE sound propagation models in the Cartesian coordinates. The first model was implemented with a split-step Fourier algorithm to obtain sound pressure, with a higher-order approximation which included cross terms, and with the free-space square-root Helmholtz operator and the medium phase speed anomaly to the square-root Helmholtz operator. The second model used higher-order operator splitting which resulted in a tridiagonal formulation, allowed a marching algorithm similar to the alternating direction implicit (ADI) method and retained cross-multiplied operator terms that had been previously neglected. To achieve a wide-angle capability, two cross terms with Y and Z in the splitting were introduced as shown below.

In 2013, Lin[79] derived a tangent linear solution for the 3D parabolic wave equation for the case of small variations of the sound speed in the medium, by using a higher-order square-root operator splitting algorithm. Moreover, he proposed and discussed the applications of associated adjoint models for acoustic inversions. Meanwhile, 3D PE models in Cartesian and cylindrical coordinates using the split-step Fourier method were presented by Lin et al.[80] Unlike the Cartesian model, the cylindrical mode has non-uniform resolution throughout the domain. Two different methods containing the fixed arc-length grid method and the increasing grid points in azimuth were adopted to achieve more uniform resolution in the cylindrical PE model.
In 2016, Sturm[81] handled a leading-order cross-multiplied term which was similar to that in Lin’s model[78] to modify the foregoing 3D PE model[74] in cylindrical coordinates. He neglected azimuthal variations of the index of refraction, assumed that operators X and Y commute, thus leading to the following approximation:
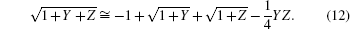
Compared with developments of the 3D fluid PE models, researches on the 3D elastic PE models are short of attention, because it is very difficult and complex. In 1998, Lee et al.[82] developed a 3D mathematical model for handling environmental interactions in the ocean between a fluid medium and an elastic bottom. After that, Nagem and Lee[83] extended the above model to consider an irregular fluid-elastic interface. They derived a construction of a complete set of 3D fluid-elastic wave equations, including the irregular interface, in a form suitable for stable numerical solution and compared the fluid-elastic irregular interface with that in the horizontal case.
In order to test reciprocity, convergence, and stability of 3D PE model, Smith[84] presented the results of an established split-step Fourier PE model and examined some test cases such as a randomly sloping bottom with ocean parameter variations and a shallow water profile perturbed by internal waves over a flat, homogeneous bottom. To examine the influence of environmental uncertainty on the details of the propagation, random perturbations were introduced to analyze sound propagation effects. Considering narrow-angle azimuthal coupling, a modified split-step Padé parabolic-equation model was implemented by Arvelo and Rosenberg[85] which was used to evaluate the effect of 3D propagation on the performance of a matched-field processor.
Hsieh et al.[86] studied the azimuthal limitation of the 3D PE approximation in cylindrical coordinate in 2007 and put forward the theoretical derivation estimating the azimuthal limitation. For analyzing the azimuthal wide angle capability, they started with the derivation of the model decomposition and illustration of the propagation angles in horizontal plane and presented the narrow and wide angle PE approximations. The azimuthal propagation angle limitation was demonstrated with the phase error estimation. In 2009, Chiu et al.[87] studied 3D acoustic effects using two parabolic equation models FOR3DW and MOS3DPEF, which was based on analysis of measured ocean data in the ASIAEX SCS. The TL comparison between Nx2D and 3D calculations demonstrated the 3D effects. The 3D effects in the acoustic field were caused by variations in topography of the shelf break and in the water column due to the internal waves. Numerical simulations showed that the nonlinear internal wave front caused severe horizontal refraction for higher modes. Chiu et al.[88] also analyzed ship noise data over a submarine canyon, which were obtained during an ocean acoustic and physical oceanography experiment in 2009, and revealed an intensification of the near-surface sound intensity. A Cartesian 3D parabolic equation (PE) program was used to study the sound in the submarine canyon, indicating that the intensification was caused by 3D sound focusing by the concave canyon seafloor.
In 2012, Ballard[89] applied an acoustic propagation which was based on a 3D adiabatic mode technique where the horizontal refraction equation was solved using a parabolic equation in Cartesian coordinates to predict measurements of 3D effects recorded off the southeast coast of Florida. Research results showed the topography of the seafloor played the largest role in controlling horizontal refraction effects, whereas the range-dependent sediment properties had the strongest influence on the received level. The variabilities in the arrival angle and received level of the measured signal were discussed with a modal decomposition of the field. Lee and Chen[90] introduced a Predictor-Corrector Method to examine the accuracy of the simulated results. Moreover, the procedure can improve the result until it became suitably accurate. The Predictor-Corrector method was used to improve the accuracy of a 3D PE model.
As a remarkable study, Sturm et al.[91] carried out laboratory scale measurements of long range across-slope acoustic propagation in a 3D wedge-like environment to demonstrate the validity of a fully 3D parabolic equation based model. The measured data containing strong 3D effects like mode shadow zones and multiple mode arrivals, are in quantitative agreement with theoretical and numerical predictions in the time and in the frequency domain.
In 2014, during an experiment conducted in the Northwestern Pacific by Qin et al.,[92] an interesting phenomenon was observed that the energy of the received signal around the sound channel axis is much higher than those of other depths. Numerical results by RAM were in consistence with experimental data.
Pan et al.[93] in 2014 studied the effects of the offshore thermocline in the East China Sea on the acoustic field. The acoustic field was shown to be greatly affected by the seasonal change of the thermocline. Besides, the thermocline gives a more forceful influence on the low-frequency acoustic field than the high-frequency acoustic field.
Miles et al.[94] in 2003 presented a variable depth step implementation of RAM for modelling forward scattering from a rough sea surface. The subsequent effect of rough boundary scattering on the replica correlation process was investigated.
A time-evolving rough sea surface model was combined with a rough surface formulation of a parabolic equation model for predicting time-varying acoustic fields in 2012 by Senne et al.[95]
Mesoscale oceanography, including internal waves, ocean fronts and eddies can have a significant effect on sound propagation in underwater acoustics. These phenomena often occur and change the environmental distributions such as temperature and sound profiles which result in the changes of sound propagation characteristics in ocean waveguides. Some parabolic equation models are used to analyze the various effects of mesoscale phenomena on sound propagation.
In 2003, Flatté and Vera[96] used the parabolic equation to estimate and quantify the fluctuations of an acoustic signal traveling which were caused by ocean internal waves. They behave like sound propagations at 250 Hz with a maximum range of 1000 km and presented a comparison between ocean-acoustic fluctuations in PE simulations and corresponding results from integral approximations.
In 2009, Zhang et al.[97] analyzed the mesoscale eddy acoustic fields in the South China Sea based on the measured CTD data and found that the mesoscale eddies had a significant effect on sound propagation. Ma et al.[98] investigated the influences of shallow water solitary wave on sound transmission loss using the three-dimensional PE model For3D[29] and compared the performances of CBF, MVDR and MUSIC in ocean with the mesoscale eddies.
In 2016, Heaney and Campbell[99] used a fully 3D parabolic equation model to examine the influence of mesoscale oceanography, including ocean fronts and eddies. A narrowband seismic wave transmission from the Kerguellen Plateau to the South Indian Ocean (a distance in between is 9100 km), was simulated by the 3D PE model. Numerical results indicated the refraction due to mesoscale oceanography had a significant influence on low-frequency sources localization, for example seismic or nuclear test events. Qin et al.[100] used the three-dimensional adiabatic mode parabolic equation model to analyze the horizontal refraction caused by internal waves and also by a coastal wedge.
Smith[101] in 2008 introduced both a parabolic equation model and a normal mode model for computing acoustic particle velocity. Ma et al.[102] in 2009 extended the model FOR3D to calculate vector acoustic field. the two studies are both limited to the assumption of a fluid bottom.
Zhang et al.[103] in 2010 implemented a model for vector acoustic field calculation, by combining the approach to operator inversion with the modified HEPE model. This idea was first proposed by Outing.[104] In 2011, Zhang et al.[105] studied the effects on distribution of vector fields for different source frequencies and source depths.
Collins et al.[10,11] presented a two-way PE model and a two-way elastic PE model in 1992 and 1993 respectively, which constructed the foundation for computing the back-scattering field and reverberation field by PE method.
In 2000, Zhu and Bjørnø[106] proposed a two-way 3D PE model in cylindrical coordinates. In 2001, Zhu[107] applied this model to reconstructing images and underwater targets.
In 2002, Lingevitch and LePage[108] presented a two-way parabolic equation that accounts for multiple scattering. In 2010, Lingevitch and LePage[109] applied this model to the problem of modelling rough interface reverberation.
In the 21st century, contributions to extending the capabilities of PE method are great number (more than 100), and they mainly focus on elastic PE models, 3D PE models and techniques to improve the accuracy or efficiency of these models. Also, efforts are made to expand the scope of PE applications, like computing back-scattering fields and reverberation fields. Therefore, PE methods have been capable of handling much more complicated propagation problems than ever.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 | |
| 52 | |
| 53 | |
| 54 | |
| 55 | |
| 56 | |
| 57 | |
| 58 | |
| 59 | |
| 60 | |
| 61 | |
| 62 | |
| 63 | |
| 64 | |
| 65 | |
| 66 | |
| 67 | |
| 68 | |
| 69 | |
| 70 | |
| 71 | |
| 72 | |
| 73 | |
| 74 | |
| 75 | |
| 76 | |
| 77 | |
| 78 | |
| 79 | |
| 80 | |
| 81 | |
| 82 | |
| 83 | |
| 84 | |
| 85 | |
| 86 | |
| 87 | |
| 88 | |
| 89 | |
| 90 | |
| 91 | |
| 92 | |
| 93 | |
| 94 | |
| 95 | |
| 96 | |
| 97 | |
| 98 | |
| 99 | |
| 100 | |
| 101 | |
| 102 | |
| 103 | |
| 104 | |
| 105 | |
| 106 | |
| 107 | |
| 108 | |
| 109 | |
| 110 |



