† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11125420, 11434012, and 41561144006) and the Knowledge Innovation Program of the Chinese Academy of Sciences.
This paper presents a three-dimensional (3D) coupled-mode model using the direct-global-matrix technique as well as Fourier synthesis. This model is a full wave, two-way three-dimensional model, and is therefore capable of providing accurate acoustic field solutions. Because the problem of sound propagation excited by a point source in an ideal wedge with perfectly reflecting boundaries is one of a few three-dimensional problems with analytical solutions, the ideal wedge problem is chosen in this work to validate the presented three-dimensional model. Numerical results show that the field results by analytical solutions and those by the presented model are in excellent agreement, indicating that the presented model can serve as a benchmark model for three-dimensional sound propagation problems involving a planar two-dimensional geometry as well as a point source.
Modeling three-dimensional (3D) sound propagation is of great importance in underwater acoustics. A variety of approaches have been applied to this problem. Finite difference and finite element methods seem to be the most suitable methods for this problem. However, the extraordinarily large computational size might make it unrealistic to apply these methods to large-scale sound propagation. A significant effort has gone into modeling 3D sound propagation based on the parabolic equation method.[1–3] The normal mode method is another choice for this problem.[4] Some hybrid approaches, such as the adiabatic mode-parabolic equation method,[5] have also been presented in recent years.
Generally it is very intensive computationally to obtain the full solution of the acoustic field in a 3D waveguide. The problem becomes less complex if the waveguide is two-dimensional. Specifically, in this case the 3D field can be obtained by combining a two-dimensional (2D) model and Fourier synthesis.[6]
A 2D coupled-mode model was developed by Luo et al.,[7] which is referred to as DGMCM2D hereafter in this paper. Unconditional stability and great accuracy are key features of this model. The unconditional stability is achieved by applying the direct-global-matrix approach in combination with an appropriate normalization scheme. This model is capable of handling two-dimensional problems with either a point source in cylindrical geometry or a line source in plane geometry. Especially, appropriate source conditions are introduced in the formulation for the line-source problem in plane geometry.[7] As a result, this model is capable of addressing the scenario where a line source is located in a range-dependent region, for example, on top of a sloping bottom.
An exact solution in the form of uncoupled normal modes was proposed by Buckingham for the acoustic field excited by a point source in an ideal wedge-shaped ocean with perfectly reflecting boundaries.[8] In this solution, each mode coefficient is the sum of two integrals, representing the image field from the source plus images, and the diffraction field arising from diffraction by the apex.
Another analytical solution for sound propagation in an ideal wedge-shaped ocean was derived by Luo et al.[9] This solution is achieved by combining the analytical solution to the 2D ideal wedge problem with a line source[10] and Fourier synthesis.
This paper presents a 3D full wave coupled-mode model, hereafter referred to as DGMCM3D, for sound propagation in a waveguide with a planar 2D geometry. First, we give the formulation of this model, followed by details on the inverse Fourier transform and integration contour chosen in this model. Then we give a brief review of the 2D coupled-mode model DGMCM2D, which applies the direct-global-matrix technique, for sound propagation in a 2D planar waveguide with a line source. We also describe briefly the analytical solutions for the acoustic field excited by a point source in a wedge-shaped ocean with perfectly reflecting boundaries. Section 3 is devoted to validation of the proposed 3D coupled-mode model, DGMCM3D, through two numerical examples. Considering that exact solutions are present for 3D sound propagation excited by a point source in an ideal wedgelike ocean with perfectly reflecting boundaries, we choose this problem to validate the presented model. In numerical examples, both the pressure-release bottom case and the rigid bottom case are considered.
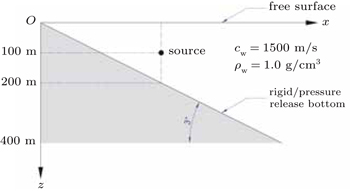
Consider the problem illustrated in Fig.
 | Fig. 1. Schematic diagram of the 3D problem involving a waveguide with a planar 2D geometry and a point source. The surface is pressure-release and the bottom is pressure-release or rigid. |
In Cartesian coordinates, with the assumption that the point source is located in the vertical plane y = 0, that is, the source position is (xs, 0, zs), the 3D Helmholtz equation is[11]

In this method, the following Fourier transform pairs are adopted:
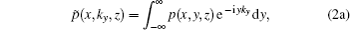



By comparing Eq. (

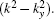
Once a sequence of the spectrum p̃(x, ky, z) is obtained, we can compute p(x, y, z) with the inverse Fourier transform. However, because p̃(x, ky, z) has singularities on the real ky axis, this model evaluates the integral in Eq. (

In addition, with symmetry, it can be shown that the inverse Fourier transform in Eq. (

In the model DGMCM3D, we choose δ = 1/(6Δs) with Δs = (kmax − kmin)/(Ns − 1), and the contour offset ε = 3Δs/(2π log e), with Ns denoting the total number of sampling points in the wavenumber space.
Below we give a brief review of the 2D direct-global-matrix coupled-mode model DGMCM2D for the line-source problem in plane geometry. See Refs. [7] and [12] for details.
In Cartesian coordinates, the Helmholtz equation with a line source located at (xs, zs) is[7]

As illustrated in Fig.

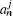


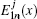


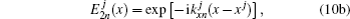
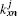
 | Fig. 3. Schematic diagram of a 2D range-dependent problem with a line source in plane geometry. The line source can be located at an arbitrary range, for instance, on top of a sloping bottom. |
Modal amplitudes





The coupling matrices in segment j, 



In addition, perfectly reflecting boundaries are considered in this work, and hence we have analytical expressions for the modal solutions and the coupling matrices. Thus, the eigenfunctions are in the form
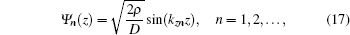


For the pressure-release bottom case, we have the following closed-form expressions for 







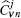




The problem of 3D sound propagation in an ideal wedge-shaped ocean is illustrated in Fig.
The 3D Helmholtz equation in cylindrical coordinates is[9,11]

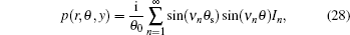


As pointed out in Ref. [8], the solution in Eq. (

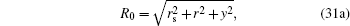

It is clear that a takes its maximum value of 1/2 when r = rs and y = 0.
The authors also derived another analytical solution for the 3D ideal wedge problem using Fourier synthesis in combination with the well-established analytical solution for the 2D line-source ideal wedge problem.[9,10] This analytical 3D solution is of the same form as that in Eq. (

As y ≠ 0, both of the integrands in Eqs. (
In this work, sound propagation is expressed in transmission loss (TL) in dB re 1 m defined as


In this section we consider the ideal wedge problem with two different wedge angles: one is 3° and the other is approximately 2.86°. For both wedges the bottom is either pressure-release or rigid. From Subsection 2.2, for the 3° wedge problem, because the wedge angle is a submultiple of π/2, and of course also a submultiple of π, for both pressure-release bottom and rigid bottom cases, the diffraction field is identically zero and hence the image solution is sufficient to provide benchmark solutions. However, for the 2.86° wedge problem, since the wedge angle is neither a submultiple of π nor π/2, the diffraction field is not identically zero for the pressure-release bottom case or the rigid bottom case. Thus, for the 2.86° wedge problem, we need to apply the analytical total solution with the integral given in Eq. (
Note that the waveguides in the numerical examples considered in this paper are ideal waveguides involving a homogeneous water column, a pressure-release sea surface, and a pressure-release or rigid bottom. Closed-form expressions are present for the local modal solutions as well as coupling matrices, and these closed-form expressions are used in DGMCM3D in this work to avoid numerical errors in that regard. For general realistic problems, a numerical method should be adopted to compute the local modal solutions and coupling matrices.
It should be pointed out that although a wedge-shaped ocean is considered in the numerical examples in this paper, the model DGMCM3D is not limited to this scenario. As described in Section 2, DGMCM3D is capable of solving sound propagation in a general waveguide with a planar 2D geometry, and the 2D planar wedge is just a special case of such waveguides.
This problem is illustrated in Fig.
First, we consider the pressure-release bottom case. For this ideal wedge problem, because the bottom is pressure-release and the wedge angle is a submultiple of π, the diffraction field is identically zero. Transmission loss along the range with a fixed cross-range and depth computed by the analytical total solution, the analytical image solution, and DGMCM3D is shown in Fig.
Transmission loss in a vertical plane computed by the analytical image solution (equivalent to the analytical total solution for this specific problem) and by DGMCM3D is shown in Fig.
In addition, transmission loss in a horizontal plane is shown in Fig.
 | Fig. 8. TL in the horizontal plane z = 30 m computed by (a) the analytical image solution and (b) DGMCM3D. |
Then we consider the rigid bottom case. For this ideal wedge problem, since the bottom is rigid and the wedge angle is a submultiple of π/2, the diffraction field is identically zero. Transmission loss along the range with a fixed cross-range and depth computed by the analytical image solution, the analytical total solution, and DGMCM3D is shown in Fig.
Transmission loss in a vertical plane computed by the analytical image solution (equivalent to the analytical total solution in this specific problem) and by DGMCM3D for this 3° wedge problem with a rigid bottom is shown in Fig.
In addition, transmission loss in a horizontal plane is shown in Fig.
The original Acoustical Society of America (ASA) benchmark wedge[13] was extended to a 3D version by Deane and Buckingham.[14] Note that in Ref. [14] a penetrable wedge was considered, whereas in this paper the boundaries of the wedge are perfectly reflecting. The 2.86° ideal wedge problem is illustrated in Fig.
For this ideal wedge problem, the wedge angle is neither a submultiple of π nor a submultiple of π/2. As a result, the diffraction field is not identically zero for either the pressure-release bottom case or the rigid bottom case. Hence, the analytical total solution, rather than the analytical image solution, should be used to provide benchmark field solutions.
For this 2.86° wedge problem, first we consider the pressure-release bottom case. Transmission loss in vertical planes y = 0 km and y = 10 km by the analytical solutions and DGMCM3D are shown in Fig.
 | Fig. 15. TL in the horizontal plane z = 30 m by (a) the analytical image solution, (b) the analytical total solution, and (c) DGMCM3D for the 2.86° wedge problem with a pressure-release bottom. |
Then we consider the rigid bottom case. Transmission loss in vertical planes y = 0 km and y = 10 km by the analytical image solution, the analytical total solution, and DGMCM3D are shown in Fig.
A full wave 3D coupled-mode model is presented in this paper, which is capable of computing acoustic fields excited by a point source in a waveguide with a planar 2D geometry. This 3D model is based on Fourier synthesis in combination with the 2D coupled-mode model DGMCM2D. When dealing with problems with an ideal waveguide involving a homogeneous water column as well as perfectly reflecting boundaries, closed-form expressions for the local modal solutions as well as coupling matrices are used in this model to avoid numerical errors in that regard. However, for realistic waveguide problems, a numerical method should be adopted to compute the local modal solutions and coupling matrices instead.
The presented model DGMCM3D is validated through two numerical examples, both of which involve a point source and an ideal wedge-shaped ocean consisting of a homogeneous water column and perfectly reflecting boundaries. Analytical solutions are present for such 3D ideal wedge problems, and they are used in this work to provide benchmark solutions. The wedge angle of the first problem is 3°, which is a submultiple of π and also π/2, and hence the diffraction field is identically zero for both the pressure-release bottom case and the rigid bottom case. The second problem is actually an extension of the 2D ASA benchmark wedge problem, where the wedge angle is approximately 2.86°. In this problem, since the wedge angle is neither a submultiple of π nor a submultiple of π/2, the diffraction field cannot be neglected when applying the analytical solutions. For both numerical examples, excellent agreement is observed between the results by the analytical total solution and those by DGMCM3D, indicating that the model DGMCM3D is very accurate, regardless of whether the diffraction field is identically zero or not.
Note that although we concentrate on the wedge-shaped ocean in this paper, the model DGMCM3D is not limited to this scenario. As a matter of fact, DGMCM3D is suitable for treating sound propagation in a general waveguide with a planar 2D geometry.
In conclusion, an accurate 3D coupled-mode model is developed. This model can serve as a benchmark model for 3D sound propagation excited by a point source in an ideal waveguide with a planar 2D geometry.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 |