† Corresponding author. E-mail:
Project supported by the National Basic Research Program of China (Grant No. 2012CB921504), the National Natural Science Foundation of China (Grant No. 11474160), the Fundamental Research Funds for the Central Universities, China (Grant No. 020414380001), the State Key Laboratory of Acoustics, Chinese Academy of Sciences (Grant No. SKLA201609), and the Priority Academic Program Development of Jiangsu Higher Education Institution, China.
Anisotropic metamaterial with only one component of the mass density tensor near zero (ADNZ) is proposed to control the sound wave propagation. We find that such an anisotropic metamaterial can be used to realize perfect bending waveguides. According to a coordinate transformation, the surface waves on the input and output interfaces of the ADNZ metamaterial induces the sound energy flow to be redistributed and match smoothly with the propagating modes inside the metamaterial waveguide. According to the theory of bending waveguide, we realize the “T”-type sound shunting and convergence, as well as acoustic channel selection by embedding small-sized defects. Numerical calculations are performed to confirm the above effects.
The acoustic properties exhibited by metamaterials are remarkable, and various amazing phenomena have been discovered in previous studies on metamaterials,[1–12] such as negative refraction,[1] negative Doppler effect,[2] and acoustic cloaking.[3–7] Metamaterial with parameters near zero are also an important and intriguing material.[13,14] Due to the fact that the equivalent parameters of metamaterial can be changed by simply adjusting the structure parameters, we can obtain not only the negative-index metamaterial with both negative density and bulk modulus,[15–17] but also the zero-index metamaterial (ZIM) with zero density and/or zero reciprocal of bulk modulus.[18,19] Recently, density-near-zero (DNZ) metamaterial and index-near-zero (INZ) metamaterial have aroused growing interest and various applications have been proposed.[20–28] Bongard et al. achieved acoustic transmission line metamaterial with zero refractive index by membranes and open channels.[20] Jing et al.,[21] Park et al.,[22] and Fleury and Alu[23] achieved near-zero-density metamaterial by using membrane structure both in numerical analysis and experimental verification respectively. In addition, Shen et al. investigated a type of anisotropic, acoustic complementary metamaterial which consists of unit cells formed by membranes and side branches with open ends.[24] Furthermore, Xu et al. designed and fabricated an anisotropic zero-mass acoustic metamaterial lens based on clamped paper membrane units.[25]
Anisotropic DNZ (ADNZ) metamaterial with only one component of the mass density tensor near zero can be used to manipulate the sound transmission in the designed paths. Various prototypes have been demonstrated to manipulate sound transmissions, such as acoustic concentration,[29] and sound transmission through ultranarrow acoustic channels.[30] The bending waveguide effect is one of the especially interesting applications.[31–33] For conventional bending waveguide, reflection and the distortion of the wave front are often complex. Many methods have been proposed to minimize the reflection and distortion of waves.[31]
In this paper, we investigate the properties of the ADNZ metamaterial further. First we find that the ADNZ metamaterial can be introduced into a waveguide system to control sound wave propagation and realize perfect bending waveguides. Then we realize the “T”-type sound shunting and convergence which support the multi-channel communication. Furthermore, acoustic channel selection by embedding small-sized defects is also an interesting finding inspired by the theory of a bending waveguide.
As illustrated in Fig.
For convenience the time variation item e−jωt is omitted. The velocity field is given by


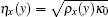
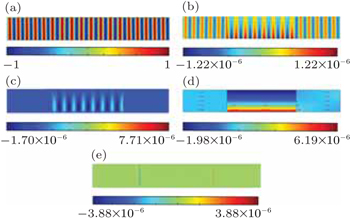
In order to verify our theoretical analysis above, the full-wave simulations are carried out by using the finite element method (FEM). Parameters in the ADNZ metamaterial are set as ρx(y) = ρ0y/[(y1 + y2)/2], ρy = ρ0/1000 and κ1 = κ0, where y1 and y2 are the upper and lower boundary of the waveguide respectively. Figure
Now we come to explain the mechanism of the acoustic energy propagating from the input interface to the output interface of the ADNZ metamaterial. The time-averaged acoustic energy flux density, also known as the acoustic intensity in the x direction Ix = 0.5Re(vxp*) should be proportional to 1/ρx(y) as vx(y) is proportional to 1/ρx(y) and the pressure is constant. Therefore, the acoustic energy flow in the x direction is larger than in the lower ρx(y) region as shown in Fig.
With the above results of a straight waveguide of ADNZ metamaterial, it would be interesting to investigate the cases for bending waveguides. As illustrated in Fig.
Furthermore, it is not limited to the semicircular channel which can make wave propagation perfect, we can make the ADNZ metamaterial into other shapes such as “T” shape as shown in Fig.
More interestingly, the total reflection can be achieved by embedding ideal soft defects in ADNZ metamaterial, which can be used to realize an acoustic switch as shown in Fig.
In this work, perfect bending waveguides with ADNZ metamaterial are realized in theory and in simulation. Theoretical analyses reveal that the key to ensuring the total transmission in bending waveguides is the surface wave, which redistributes the sound energy flow. With the support of the theory of bending waveguide, “T”-type sound shunting and convergence can support multi-channel communication, and the acoustic channel selection which is affected by the small-sized embedded defects can be used to realize acoustic switch. In practical applications, the bending waveguide achieved by anisotropic near-zero parameters can be possibly implemented by employing membrane-type acoustical metamaterial with properly tuned structural parameters, [24,25] which is the goal of our next work.