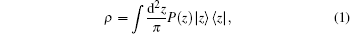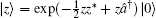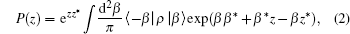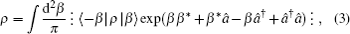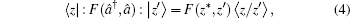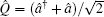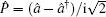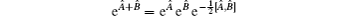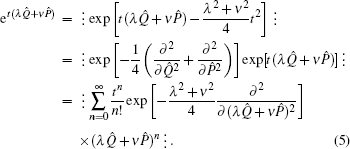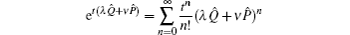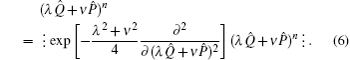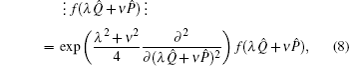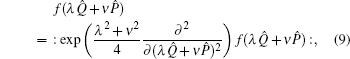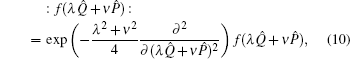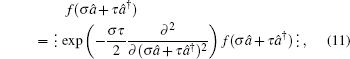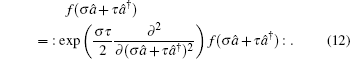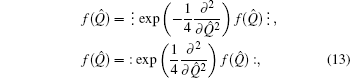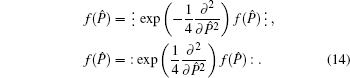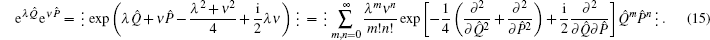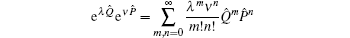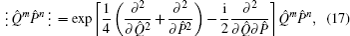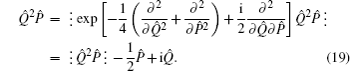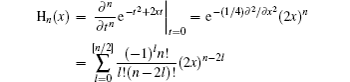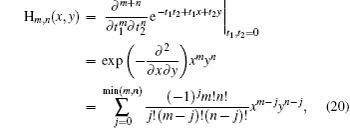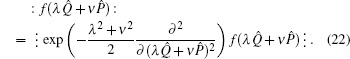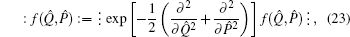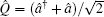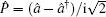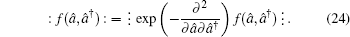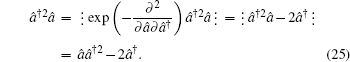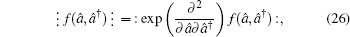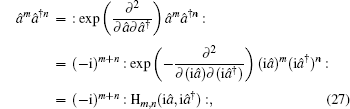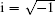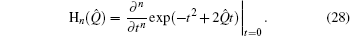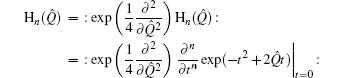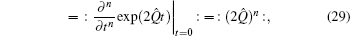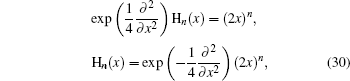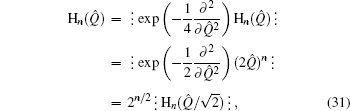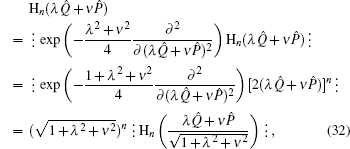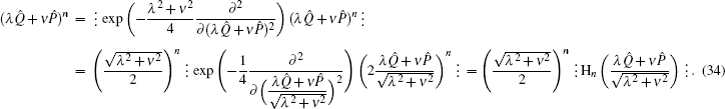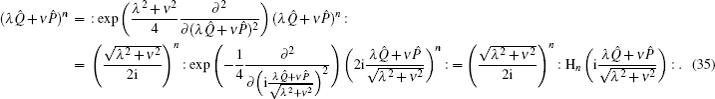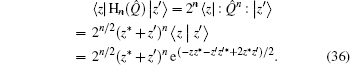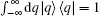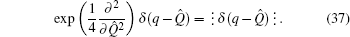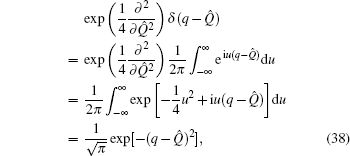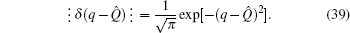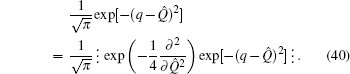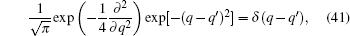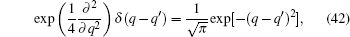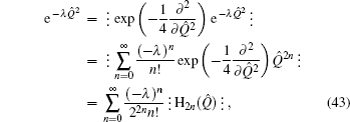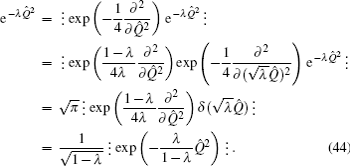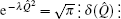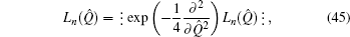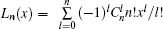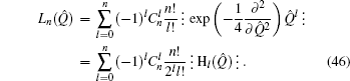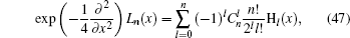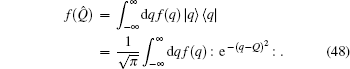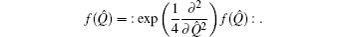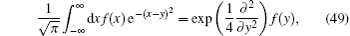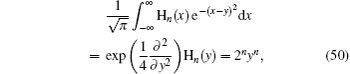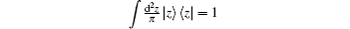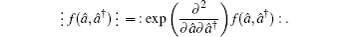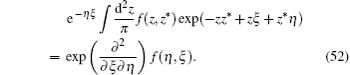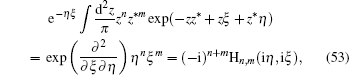New approach for anti-normally and normally ordering bosonic-operator functions in quantum optics
1. IntroductionThe operator ordering problem,[1,2] which bothers people from time to time, plays an important role in constructing quantum mechanical operators[3] and describing the phase space of quantum mechanics.[4] The operator ordering problems are often encountered in quantizing a classical function and in calculating various matrix elements of operators. In quantum optics, operator ordering problems arise in converting operator master equations into c-number equations in phase space. As is well known, the anti-normally ordered expansion of an operator is very useful in calculating the P-representation of the density operator, because the P-representation of a density operator is[5]
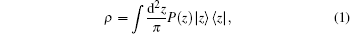
where
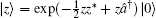
is the coherent state,
[6–8] ↠and
â are bosonic creation and annihilation operators respectively, obeying [
â,
â†] = 1. The inverse transformation of Eq. (
1) reads
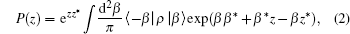
which is the Mehta formula.
[9] By substituting Eq. (
2) into Eq. (
1) we have
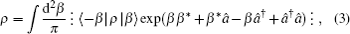
where the symbol ⁝ ⁝ represents the anti-normal ordering (all
â stand on the left of all
â†). Equations (
2) and (
3) imply that its
P-representation can be obtained immediately once the anti-normal ordering form of a quantum operator is given. The normally ordered form of an operator is closely related to handling miscellaneous calculations of expectation values of observables in the coherent states, because the matrix elements of the normally ordered operator function :
F(
â†,
â) : in coherent states directly yields
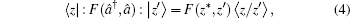
where the symbol ∶ ∶ denotes the normal ordering (all
↠stand on the left of all
â). Therefore, it is an important topic to obtain the anti-normal and normal ordering form of the operators in quantum optics.
To the best of our knowledge, there are three main methods of handling operator ordering problems in most published reports, such as the Lie algebra method,[10] Louisell’s differential operation method via the coherent state representation,[11] and the newly developed technique of integration within ordered product (IWOP) of operators.[12–15] However, from the above mentioned reports, we notice that when the authors derived some operator normal ordering forms by using the IWOP technique, they had to first know the completeness relation of the eigenvector of the operator to be ordered as a pure Gaussian integration in the normal ordering form, and then make use of some complex mathematical integral formula. In this work, in order to avoid these inconveniences, we report several new formulas for anti-normally and normally ordering bosonic-operator functions. Namely, we directly utilize the Baker–Hausdorff formula and differential method of operators to derive new and neat formulas for anti-normally and normally ordering bosonic-operator functions. Using these formulas we can arrange a bosonic-operator function f(λQ̂ + νP̂) in its anti-normal and normal ordering conveniently, where 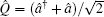 and
and 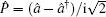 are the coordinate operator and momentum operator respectively. Furthermore, the mutual transformation formulas between anti-normal ordering and normal ordering are derived too. Based on these operator formulas, some new differential relations and some useful mathematical integral formulas are easily derived without really performing these integrations.
are the coordinate operator and momentum operator respectively. Furthermore, the mutual transformation formulas between anti-normal ordering and normal ordering are derived too. Based on these operator formulas, some new differential relations and some useful mathematical integral formulas are easily derived without really performing these integrations.
2. The differential operation for transforming f(λQ̂ + νP̂) to ⁝f(λQ̂ + νP̂)⁝ and : f(λQ̂ + νP̂):In this section we discuss how an operation can transform f(λQ̂ + νP̂) to ⁝ f(λQ̂ + νP̂) ⁝ and :f(λQ̂ + νP̂):. To begin with, we study the exponential operator et(λQ̂+νP̂). By virtue of the Baker–Hausdorff formula
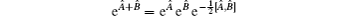
([
Â,[
Â,
B̂]] = [
B̂,[
Â,
B̂]] = 0), we can obtain the anti-normal ordering form of e
t(λQ̂+νP̂) as follows:
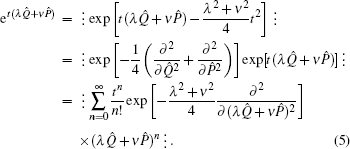
With considering the expansion of
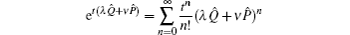
and comparing the terms with the same power of
t on both sides of Eq. (
5), we easily obtain a neat formula as follows:
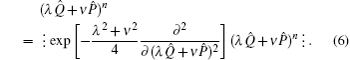
So, for any function
f(
λQ̂ +
νP̂) which can be expanded as a power series of (
λQ̂ +
νP̂)
n, it follows that

which is just the formula for converting bosonic-operator function
f(
λQ̂ +
νP̂) into its anti-normal ordering. Noticing that
∂/
∂Q̂,
∂/
∂P̂,
∂/
∂ (
λQ̂ +
∂νP̂) are merely differential operations, not quantum mechanical operators. Their consequences are permutable and they may enter into or go out of the symbols: : and ⁝ ⁝ freely.
Following Eq. (7), we can obtain
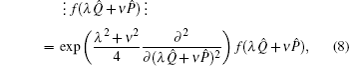
which is the new approach to eliminating the symbol ⁝ ⁝ from ⁝
f(
λQ̂ +
νP̂) ⁝.
Similarly, we may obtain that
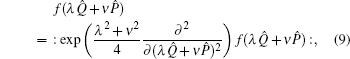
which is just the differential formula for converting bosonic-operator function
f(
λQ̂ +
νP̂) into its normal ordering. Equation (
9) yields that
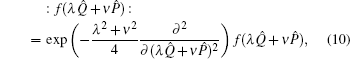
which is the new approach to eliminating the symbol ⁝ ⁝ from :
f(
λQ̂ +
νP̂):.
Moreover, by introducing  and
and  , we can rewrite Eqs. (7) and (9) as
, we can rewrite Eqs. (7) and (9) as
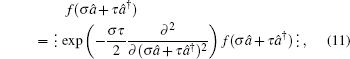
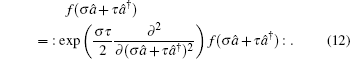
Especially, when
λ = 1 and
ν = 0, we immediately obtain
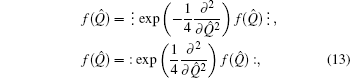
and when
λ = 0 and
ν = 1, we have
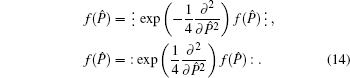
In Refs. [
16] and [
17], with the help of some complex mathematical integral formulas, the IWOP technique and intermediate coordinate-momentum representation are used. In Ref. [
18], their results are merely the ordered form of some operators such as
Q̂n,
P̂n, and (
λQ̂ +
νP̂)
n. Without doubt, we provide a new kind of operator formulas for anti-normally and normally ordering bosonic-operator functions including
f(
Q̂),
f(
P̂), and
f(
λQ̂ +
νP̂), and our approach shows its features of simpleness, neatness and directness.
3. Differential operation for transforming Q̂mP̂n (P̂mQ̂n) to its anti-normal and normal orderingNow we discuss how to transform Q̂mP̂n (P̂mQ̂n) into its anti-normal and normal ordering. Considering the exponential operator eλQ̂eνP̂ and by virtue of [Q̂,P̂] = i, [â,â†] = 1, and the Baker–Hausdorff formula, we have
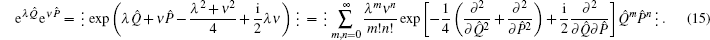
With considering the expansion of
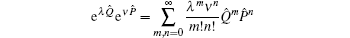
and comparing the terms with the same powers of
λ and
ν on both sides of Eq. (
15), we easily obtain the neat formula

which is just the differential formula for converting bosonic-operator
Q̂mP̂n into its anti-normal ordering. Following it, we have
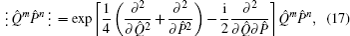
which is the new approach to eliminate the symbol ⁝ ⁝ from ⁝
Q̂mP̂n ⁝. In a similar way, the normal ordering expansion of
Q̂mP̂n, and the anti-normal and normal ordering expansions of
P̂mQ̂n are described respectively as

For example
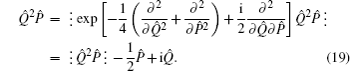
Moreover, using the Hermite polynomial
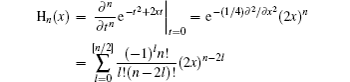
and the two-variable Hermite polynomial
[19,20]
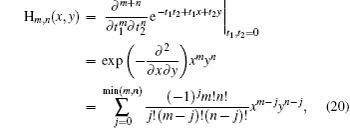
we may derive that

which is the anti-normally ordered expansion of
Q̂mP̂n. In fact, equations (
16)–(
18) provide the mutual transformation formulas between the quantum mechanical operators whose all
Q̂ (or
P̂) stand on the left hand of all
P̂ (or
Q̂) and their anti-normal and normal ordering.
4. Mutual transformation formulas between anti-normal and normal orderingFrom Eqs. (7) and (9) we can derive the mutual transformation between anti-normal and normal ordering, i.e.,
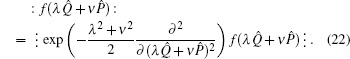
Since
∂2/
∂Q̂2 +
∂2/
∂P̂2 = (
λ2 +
ν2)
∂2/
∂(
λQ̂ +
νP̂)
2, the above equation can be rewritten as
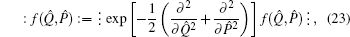
which is the transformation formula for converting a normally ordered operator function into its anti-normally ordered form. Here, we have replaced
f(
λQ̂ +
νP̂) with an arbitrary operator function
f(
Q̂,
P̂) because it is in an ordered product symbol. Using
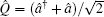
and
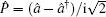
, equation (
23) may be represented as
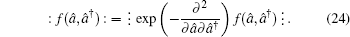
For example,
â†2â, which is normal ordering, then
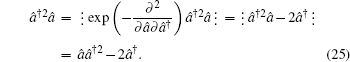
The reciprocal transformation of Eq. (
24) reads
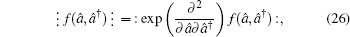
which is the transformation formula for converting an anti-normally ordered operator function into its normally ordered form. For example,
âmâ†n is anti-normal ordering, and its compact form of normal ordering can be obtained as
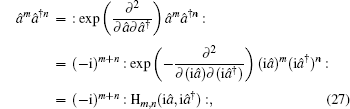
where
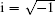
and H
m,n (
x,
y) is the two-variable Hermite polynomial function.
5. ApplicationsWe now give several examples of some applications of the above operator formulas as follows.
Example 1 First of all, we consider the Hermite polynomial operator function Hn (Q̂), which is defined by
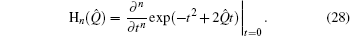
By virtue of Eq. (
13), we know that
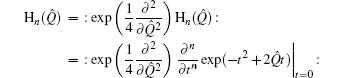
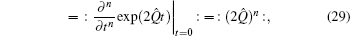
which is the normally ordered form of H
n (
Q̂). In addition, equation (
29) implies that
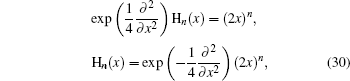
which are two new differential formulas for the Hermite polynomial H
n (
x), and will be quite useful in our work. Furthermore, the anti-normally ordered expansion of H
n (
Q̂) can be obtained, i.e.,
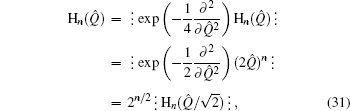
where we have used Eq. (
30) repeatedly.
Example 2 Following Eqs. (7) and (30) we have
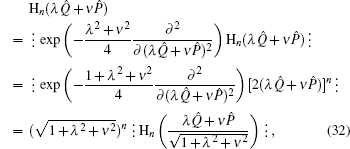
which is the anti-normal ordering form of H
n (
λQ̂ +
νP̂). In a similar way, the normal ordering expansion of H
n (
λQ̂ +
νP̂) is described as

Example 3 By using Eqs. (7) and (30), we may obtain the anti-normal ordered form of (λQ̂ + νP̂)n as follows:
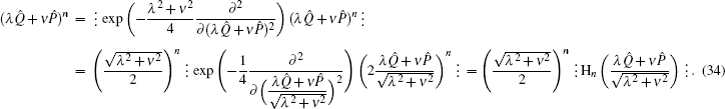
Similarly, by virtue of Eqs. (
9) and (
30), the normal ordered form of (
λQ̂ +
νP̂)
n can be obtained as
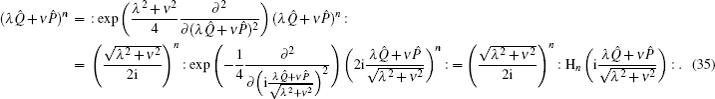
This result is Eq. (11) of Ref. [
17] and Eq. (11) of Ref. [
18]. By comparison, our approach is simple and concise.
Example 4 Using Eq. (29), we may derive the matrix elements of Hn (Q̂) in coherent states directly as
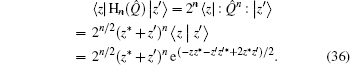
Here, our method is simple and convenient with utilizing neither the completeness relation of coordinate representation
nor any complex mathematical integral formula.
Example 5 Substituting δ(q − Q̂) for f(Q̂) in Eq. (8), it follows that
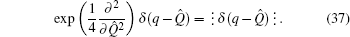
On the other hand
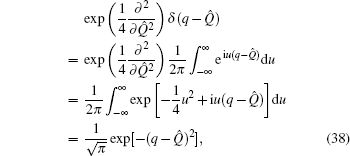
so
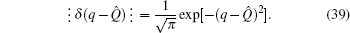
By using Eq. (
7) once again, we have
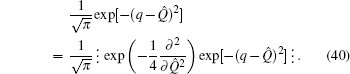
Comparing Eq. (
39) with Eq. (
40), we can obtain
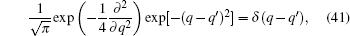
which is a new differential form of Dirac’s delta function. The reciprocal transformation of Eq. (
41) reads
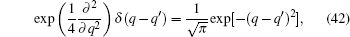
which will be useful in operator-ordering theory and special function theory.
Example 6 Replacing f(Q̂) with e−λQ̂2 in Eq. (8), we have
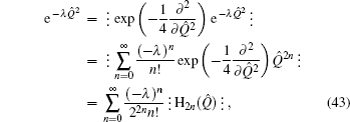
which is the anti-normal ordering form of e
−λQ̂2 for an arbitrary parameter
λ.
Imposing the condition 1 > λ > 0 yields that
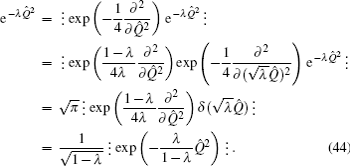
In the above calculation we have used Eqs. (
41) and (
42) repeatedly. Obviously, when
λ = 0, then e
−λQ̂2 = 1, and when
λ = 1, then
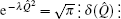
.
Example 7 Now we prove the relation between the Laguerre polynomial and the Hermite polynomial. By virtue of Eq. (7) we know
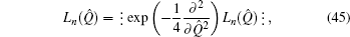
where the definition of the Laguerre polynomial is
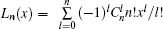
. On the other hand,
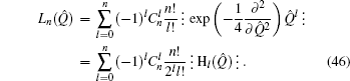
Comparing Eq. (
45) with Eq. (
46), we can obtain
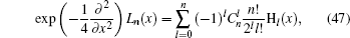
the above equation shows that the Laguerre polynomial and the Hermite polynomial are related by the differential operator

.
Example 8 Now we come to deduce a useful mathematical integral formula. By using the completeness relation of coordinate representation, we may have
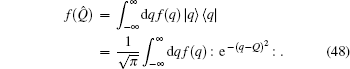
On the other hand, by virtue of Eq. (
7) we have
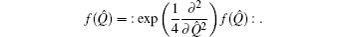
By comparison, the mathematical integral formula is given as
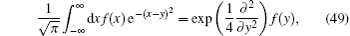
which holds true for any function
f(
x). Especially, when
f(
x) = H
n (
x), equation (
49) turns into
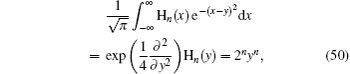
which is easily derived, without really performing the integration. By the way, Eq. (
49) can be seen as a mathematical or physical transformation.
Example 9 As a final example, using the over-completeness relation of coherent state
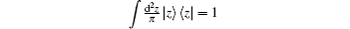
and
â|
z〉 =
z|
z〉, we have

On the other hand, it follows from Eq. (
26) that
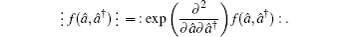
Since in the normal ordering, symbols
â and
↠are commutative, they may be treated as a
c-number. Setting
↠→
ξ and
â →
η, we easily obtain
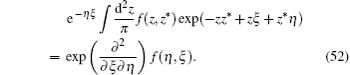
This integral transformation formula holds true for any function
f (
z,
z*). Especially, when
f (
z,
z*) =
znz*
m, we can derive the following identity:
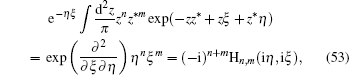
which is often used in some published reports.
6. ConclusionsIn this work, by directly employing the Baker–Hausdorff formula and the operator differential method, we find a new kind of operator formula for anti-normally and normally ordering bosonic-operator functions, which can help us transform some operators such as f (Q̂), f (P̂), f (λQ̂ + νP̂), Q̂mP̂n, and P̂mQ̂n into their anti-normal and normal ordering conveniently. As their important byproducts, the mutual transformation formulas between anti-normal ordering and normal ordering are derived too, which have the good universality. Furthermore, based on these operator formulas, some new differential relations and some useful mathematical integral formulas are easily derived without really performing these integrations. These new formulas are useful in operator-ordering theory and special function theory. By comparison, our method is simple and neat.