A magnetron has the advantages of low cost, high efficiency, and high power, so it becomes the preferred microwave source of industrial applications.^[1] An injection-locked magnetron (ILM) is the precondition of coherent power combining, which has become the focus of theory, simulation, and experiment studies in the industrial microwave applications.^[2–9] The frequency characteristic is the most important aspect of a magnetron, which can reflect the relationship between the radio frequency (RF) voltage, frequency, injection ratio, and the bandwidth with anode voltage and magnetic field. The frequency characteristics of the magnetron mainly consist of two parts: one is the frequency pulling caused by the load changes, and the other is the frequency pushing caused by the anode current.^[10] Since the injection signal plays the role of modulation in ILM,^[8,9] its frequency characteristic mainly depends on the free oscillation magnetron (FOM). So it is necessary to research the RF voltage and frequency of both FOM and ILM.

The magnetron is affected by many factors, such as orthogonal electric and magnetic fields, as well as the RF field. As it is very difficult to give analytical expressions of electronic admittance and solutions of magnetron self-consistent field equations, many approximation methods and experiments are often adopted to study magnetron.^[11–20] Slater gave approximate electron admittance expressions, which are widely used in latter investigations.^[11,12] Welch proposed the expression of a frequent pushing parameter on the voltage by studying the formation of electronic spokes, so the frequency pushing parameter can be quantified.^[13] For ILM, David presented the expressions of RF voltage and frequency by using an equivalent circuit method, which is widely adopted and developed.^[14,15] Woo obtained the time-domain amplitude and phase differential equations of high power ILM power, and performed a dual magnetron mutual-injection-locking experiment.^[16] Chen gave the steady-state expressions of RF voltage and frequency of ILM.^[17] In recent years, Tahir analyzed the modulation mechanism of the injection signal on the frequency and phase of the magnetron.^[18,19]

Despite the fact that the ILM theory has been gradually developed, the existing theories mainly focus on frequency pulling caused by the injection signal, in which the anode voltage and the magnetic field are constant. But in practical applications, the output power of the magnetron is usually adjusted by the voltage or magnetic field, and the oscillation frequency also changes, which has an important impact on both FOM and ILM. However, the present equivalent circuit theory^[14,15,17] has not been combined with the frequency pushing theory.^[13] So the frequency characteristic of the magnetron with frequency pushing cannot be theoretically calculated with its anode voltage and magnetic field. Especially, the conventional theory cannot solve the variation of the output power and frequency with the magnetic field. Therefore, it is essential to give approximate expressions of frequency and other parameters depending on the anode voltage and magnetic field. The numerical calculation of the theory and the corresponding simulation and experimental verification are also indispensable.

This paper is organized as follows. In Section 2, the expressions of the RF voltage and frequency of FOM, as well as the locking bandwidth of ILM, on the anode voltage and magnetic field are obtained by an equivalent circuit method. In Section 3, by numerical calculation, the influences of the anode voltage and magnetic field on the RF voltage, frequency, pushing parameter, and locking bandwidth are analyzed. In Section 4, three-dimensional particle-in-cell (PIC) simulation and experimental measurement are carried out to verify the results of the numerical calculations. Finally, some conclusions are drawn from the present investigation in Section 5.

The equivalent circuit model of a magnetron is shown in Fig. 1,^[14,15] where g and G represent the conductance of electron and the load, respectively; b and B are the susceptance of electron and the load; and C, R, and L are the equivalent capacitance, resistance, and inductance of the resonant cavity, respectively. The following symbols of frequency will be used: ω₀, the resonant angular frequency of the magnetron; ω′, the oscillating angular frequency of FOM; ω₁, the angular frequency of the injected signal; ω, the instantaneous angular frequency of the magnetron; while f₀, f′, f₁, and f are the corresponding frequencies.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Equivalent circuit of the magnetron.

When ω′ is close to ω₀, the resonator’s admittance is Y(ω) = 1/R + 2jC(ω′ − ω₀), where .

The oscillation circuit equation is^[16]

The real and imaginary parts of Eq. (1) represent the stability conditions of amplitude and frequency, respectively, which can be written as

When the magnetic field is constant, the approximate expression of the electron conductance given by Slater^[13] is

For simplified analysis, we assume that the DC energy of the electrons completely converts to the microwave energy and kinetic energy of the electrons. The energy relation can be written as

For a different magnetic field, if the microwave energy is constant, the DC voltage and the synchronous speed should change accordingly. When the new DC voltage and magnetic field are V_n and B_n, respectively, in order to ensure constant power is obtained in the same time, there is

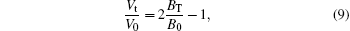
The coefficient k should be associated with V₀, B₀, and the power. This value is smaller than the DC voltage. In order to simplify the analysis, the coefficient k is ignored. So when the power is constant, the anode voltage is approximately proportional to the magnetic field.

According to Varian’s experimental data,^[10] the equal power lines of the common magnetron are drawn in Fig. 2. As shown in Fig. 2, when the power is constant, the anode voltage is approximately proportional to the magnetic field, which is consistent with the theoretical analysis.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Equal power lines of the magnetron.

If the anode voltage V_a is constant and the magnetic field changes from B₁ to B_T, the new working point’s magnetic field is B_T and the anode voltage is V_a1. So the equal power anode voltage V_ae for B₁ should be

The approximate electron susceptance of the magnetron is given by^[15]

The magnetron’s working voltage V_a should be within the limited range between its threshold voltage V_t and the cutoff voltage V_C. According to the motion of electrons and the space charge theory, the expressions of V_t and V_C can be given by

According to the formation mechanism of space charge spokes, the approximate relationship between α and the anode voltage and the RF voltage can be expressed as^[13]

Substituting Eqs. (13)–(15) and (19) into Eqs. (2) and (3) yields the steady-state RF voltage and frequency of free oscillation magnetron, which can be written as

An actual injection-locked system diagram is shown in Fig. 3. The corresponding equivalent circuit model is shown in Fig. 4. In Fig. 4, g′ and b′ represent the conductance and the susceptance of the electron, respectively. Similarly, G′ and B′ represent the conductance and the susceptance of the injection source, respectively.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. ILM system diagram.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Equivalent circuit of ILM.

The injection signal with angular frequency ω₁ (ω₁ ≈ ω₀), voltage V₁, and current I₁ is injected into the magnetron after two circulators. So the load admittance of the magnetron is divided into two parts, one is the actual load and the other is the injection signal. The reflection signal by the load can be absorbed. Therefore, the loading effect of the injection signal plays the main role.

Since G is normalized, the injection ratio can be expressed as ρ = V₁/(V_RF0 + V₁). When V_RF0 is small, V₁ is not negligible compared to V_RF0. For ILM, the oscillation circuit equation becomes

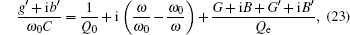
Then the new stability conditions can be written as^[17]

Similarly, the RF voltage and the operating frequency of ILM can be obtained as

The angular frequency difference between the injection signal frequency and the free oscillation frequency is Δω = |ω₁ − ω′|, while Δf is the corresponding frequency difference. The frequency difference is the biggest during the injection-locking progress. Only if Δω meets the trigonometric condition (27), the magnetron can be injection-locked. Then, the locking range is

From Eqs. (26) and (29), the influence of the anode voltage and magnetic field on the RF voltage and locking bandwidth of ILM can be analyzed. Equation (29) shows that when considering the frequency pushing effect, the locking bandwidth is wider than that of the Adler theory.

In addition, similar to the case without frequency pushing, the steady-state phase difference is independent of the initial value, which can be expressed as

When the injection power and frequency are constant, the frequency difference Δf and the locking bandwidth will change with the anode voltage and magnetic field, which may cause the failure of the injection-locked system. Therefore, it is necessary to analyze the relation between Δf, locking bandwidth, and anode voltage or magnetic field.

A six-cavity magnetron is taken as an example, whose r_a and r_c are 15.56 mm and 4.89 mm, respectively. To simplify the calculations, the load is assumed to be well matched, so B = 0. Eigenmode simulation of the magnetron shows f₀ = 940 MHz, Q_e = 150, and Q₀ = 2630. Then it can be inferred that Q_L = 141.91, C = 2.54 × 10⁻⁸ F, g = 1.057 S, and R = 17.53 Ω. b₀ has less impact on the result, so its value is set to be 0.1 S.

The threshold voltage and cutoff voltage of the magnetron are shown in Fig. 5. Meanwhile, to ensure that equation (18) is reasonable, V_a cannot be too large. Therefore, the working range is determined by the threshold voltage and the limits of Eq. (18).

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. The relation between the anode voltage and the magnetic field of the magnetron.

When the magnetic field B_T = 0.1 T, the threshold voltage is 18.8 kV. The relationship between the RF voltage and the anode voltage of FOM can be obtained from Eq. (21). According to the simulation, the port voltage is nearly 18.5% of the RF voltage. Then the output power can be obtained by

The effect of the anode voltage on the RF voltage and power of FOM is shown in Fig. 6. The change tendency of the frequency and pushing parameter of FOM with the anode voltage can be obtained from Eqs. (22) and (19), as shown in Fig. 7.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Effect of the anode voltage on the RF voltage and power of FOM.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Effect of the anode voltage on the frequency and pushing parameter of FOM.

Figure 6 shows that the RF voltage increases linearly with the anode voltage, and the power shows a quadratic growth with the anode voltage. According to Eq. (21), V_RF0 is proportional to V_a. So P_out is a quadratic function of V_a, and the growth rate increases with the increasing V_a. In order to meet the trigonometric function in Eq. (18), the ranges of V_a and B_T are limited. So in this range, the quadratic trend of the power with V_a in Fig. 6 is inconspicuous.

As seen in Fig. 7, with the increase of the anode voltage, the frequency pushing effect gradually decreases and the frequency increases. The frequency pushing reduces the frequency. It should be noted that, due to the presence of the electron admittance and frequency pushing, the oscillation frequency is always lower than the resonant frequency.

Furthermore, the other way to increase the power is to lower the magnetic field. When the anode voltage is 19.2 kV, the parameters of the magnetron are researched with varied magnetic field from 0.099 T to 0.106 T.

The change tendency of the RF voltage and output power of FOM with the magnetic field can be given by Eq. (21), as shown in Fig. 8. The change tendency of the frequency and pushing parameter of FOM with the magnetic field is shown in Fig. 9, which is obtained from Eqs. (22) and (19).

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. Effect of the magnetic field on the RF voltage and power of FOM.

Fig. 9.

	Figure Option ViewDownloadNew Window
	Fig. 9. Effect of the magnetic field on the frequency and pushing parameter of FOM.

According to Eq. (21), V_RF0 is an inverse function of the magnetic field. Therefore, the power increases with the decreasing magnetic field and the growth rate increases. Due to the parameters we selected, the range of the magnetic field is limited, so the quadratic relation in Fig. 8 is not obvious.

As seen from Figs. 8 and 9, when the magnetic field reduces, the equivalent anode voltage increases, so that the RF voltage and the resonant frequency increase, while the frequency pushing weakens. Therefore, the influence of the magnetic field on the RF voltage and frequency resonance is consistent with the anode voltage.

For ILM, the effects of the anode voltage or magnetic field on the RF voltage and locked bandwidth are also analyzed. When f₁ = 938 MHz and B_T = 0.1 T, trends of the frequency difference and locking bandwidth of ILM with the anode voltage are shown in Fig. 10, in which the injection voltage is set to be 100 V, 200 V, and 300 V respectively.

Fig. 10.

	Figure Option ViewDownloadNew Window
	Fig. 10. Effect of the anode voltage on the frequency difference and locking bandwidth of ILM.

As shown in Fig. 10, with the increase of the anode voltage, the locking bandwidth decreases, and the frequency increases. Therefore, the frequency difference decreases firstly, and then increases. However, when the voltage continues to increase, the frequency difference may be larger than the locking bandwidth, which would lead to the failure of locking. Higher injection power can increase the locking bandwidth, so it increases the anode voltage range.

When V₁ = 300 V, f₁ = 938 MHz, and B_T = 0.1 T, trends of the RF voltage and injection ratio with the anode voltage of ILM can be given by Eq. (25), as shown in Fig. 11.

Fig. 11.

	Figure Option ViewDownloadNew Window
	Fig. 11. Effect of the anode voltage on the RF voltage and injection ratio of ILM.

As can be seen from Fig. 11, when the voltage is near the threshold voltage, the RF voltage is small and the injection ratio is large. With the increase of the anode voltage, the injection ratio decreases. In addition, the RF voltage of ILM is usually smaller than that of FOM.

With the parameters we chose, when V_a = 19.15 kV, the frequency of the injection signal is very close to the frequency of FOM. At this time, the steady-state phase difference has the minimum value. And the equivalent conductance of the injection signal G′ has the maximum value. With the increase of V_a, the frequency of FOM increases and Δω decreases. The load effect of the injection signal enhances, so V_RF first decreases. With further increase of V_a, the frequency of FOM and Δω increase. Then the load effect of the injected signal weakens, V_RF gradually increases.

Similarly, when f₁ = 938 MHz and V_a = 19.2 kV, trends of the frequency difference and locking bandwidth with the magnetic field are shown in Fig. 12. Trends of the RF voltage and injection ratio with the magnetic field of ILM are shown in Fig. 13 when V₁ = 300 V.

Fig. 12.

	Figure Option ViewDownloadNew Window
	Fig. 12. Effect of the magnetic field on the frequency difference and locking bandwidth of ILM.

Fig. 13.

	Figure Option ViewDownloadNew Window
	Fig. 13. Effect of the magnetic field on the RF voltage and injection ratio of ILM.

As seen from Figs. 12 and 13, as the magnetic field decreases, the equivalent anode voltage increases. So the injection ratio and the locking bandwidth decrease. Therefore, the influence of the magnetic field on the injection ratio and the locking bandwidth is also consistent with the anode voltage.

3.1. Simulation and experiment

The injection signal can significantly influence the frequency and power of the magnetron. In our laboratory, a 2.45 GHz and 15 kW high-power continuous wave magnetron is used to perform the injection-locking experiment. A 200 W injection signal within the locking range of the magnetron is injected into the magnetron. But this system can only operate at fixed voltage and magnetic field. Therefore, it cannot be directly used to validate our theory. Since the injection signal is small, it mainly plays the role of modulation. The output power and frequency of magnetron are mainly determined by the free oscillating state. Therefore, the simulation and experimental verifications of the output power and frequency are focused on FOM.

With the help of MAGIC 3D, a kind of PIC simulation software, a magnetron model with parameters in Section 3 is built. When B_T = 0.1 T, the magnetron’s optimum operating voltage is 21 kV. Its output power is 23.5 kW and frequency is 938 MHz, which are close to our theoretical results. Therefore, by assigning reasonable parameters, the theory of this paper can give the approximate power and frequency of the magnetron.

In addition, we find that the working ranges of V_a and B_T obtained by the PIC simulation are very limited. Departing from the optimum operating point, the magnetron can hardly completely oscillate. So it is difficult to analyze the characteristics of the magnetron with variable voltage and the magnetic field by the PIC simulation. Therefore, we mainly adopt experiment data to verify the validity of the theory.

Given our experimental conditions, we only perform the experiment of FOM with a changeable magnetic field. For the variable voltage case, we adopt the experiment data of Ref. [10].

With the experimental data of Ref. [10], the power curve with the anode voltage is shown in Fig. 14. The power is approximately a quadratic function of the anode voltage. With the increase of the anode voltage, the power and its growth rate increase. So the experimental data are in good agreement with the theoretical result.

Fig. 14.

	Figure Option ViewDownloadNew Window
	Fig. 14. Experiment data of power vs. anode voltage.

In addition, a typical frequency characteristic curve in Ref. [10] shows that, before the saturation point, the frequency increases with increasing current and the growth rate becomes slow, as shown in Fig. 15. Thus, the theoretical analysis is in agreement with the typical experimental result.

Fig. 15.

	Figure Option ViewDownloadNew Window
	Fig. 15. Typical frequency characteristic curve.

A 20 kW and 915 MHz continuous wave magnetron is used to perform the experimental measurement with a variable magnetic field. When the anode voltage is 11.2 kV, trends of the output power and frequency with the magnetic field are shown in Figs. 16 and 17, respectively.

Fig. 16.

	Figure Option ViewDownloadNew Window
	Fig. 16. Experimental results of power vs. magnetic field.

Fig. 17.

	Figure Option ViewDownloadNew Window
	Fig. 17. Experimental results of frequency vs. magnetic field.

The experimental results in Fig. 16 show that, with the decrease of the magnetic field, the power and its growth rate increase. Similarly, as shown in Fig. 17, with the decrease of the magnetic field, the pushing effect weakens. The frequency increases, but its growth rate decreases. Therefore, the theory results are consistent with the experimental results and the typical frequency curve.

Note that the theoretical results do not completely agree with the experimental data and the simulation results. This is because the parameters adopted by the theoretical calculation are different from the actual ones. What is more, some approximate conclusions and statistical regularities adopted in the theoretical analysis cannot describe the actual oscillating process accurately.

The frequency characteristics of FOM and ILM are investigated. With the equivalent circuit method, the expressions of the RF voltage and frequency of FOM, as well as the locking bandwidth of ILM, on the anode voltage and magnetic field are derived. Then the frequency characteristics of the magnetron can be theoretically calculated with its anode voltage and magnetic field. The theoretical calculation results show that, with the increasing anode voltage and decreasing magnetic field, the output power and frequency of FOM increase, and the injection ratio and locking bandwidth of ILM decrease, which are consistent with the experiment results. The theory in this paper provides a theoretical guidance for the injection-locked system with variable anode voltage and magnetic field. In addition, after replacing an adjustable voltage and magnetic field power supply, the injection-locked magnetron experiment will be performed and the numerical results need further verification.