† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11172285, 11472259, and 11302217) and the Natural Science Foundation of Zhejiang Province, China (Grant No. LR13A020002).
This paper presents a lumped equivalent circuit model of the nonreciprocal magnetoelectric tunable microwave band-pass filter. The reciprocal coupled-line circuit is based on the converse magnetoelectric effect of magnetoelectric composites, includes the electrical tunable equivalent factor of the piezoelectric layer, and is established by the introduced lumped elements, such as radiation capacitance, radiation inductance, and coupling inductance, according to the transmission characteristics of the electromagnetic wave and magnetostatic wave in an inverted-L-shaped microstrip line and ferrite slab. The nonreciprocal transmission property of the filter is described by the introduced T-shaped circuit containing controlled sources. Finally, the lumped equivalent circuit of a nonreciprocal magnetoelectric tunable microwave band-pass filter is given and the lumped parameters are also expressed. When the deviation angles of the ferrite slab are respectively 0° and 45°, the corresponding magnetoelectric devices are respectively a reciprocal device and a nonreciprocal device. The curves of S parameter obtained by the lumped equivalent circuit model and electromagnetic simulation are in good agreement with the experimental results. When the deviation angle is between 0° and 45°, the maximum value of the S parameter predicted by the lumped equivalent circuit model is in good agreement with the experimental result. The comparison results of the paper show that the lumped equivalent circuit model is valid. Further, the effect of some key material parameters on the performance of devices is predicted by the lumped equivalent circuit model. The research can provide the theoretical basis for the design and application of nonreciprocal magnetoelectric tunable devices.
For magnetoelectric composite materials consisted of ferromagnetic and ferroelectric phases, the strain coupling leads to the direct/converse magnetoelectric coupling effect[1–7] in the magnetoelectric composite materials. The magnetoelectric composite materials and multiferroic film possess the capability of controlling magnetism and the ability of tuning ferromagnetic resonance by an electric field applied to the piezoelectric phase through magnetoelectric (ME) coupling.[8–13] Due to the magnetization controlled by the electrostatic field or voltage, the magnetoelectric coupling mechanism may contribute to the formation of a series of RF/microwave magnetoelectric devices[14–16] in the future, whose frequency and bandwidth are magnetoelectric tunable. At present, the magnetoelectric tunable filter,[17,18] the magnetoelectric resonator,[19,20] the magnetoelectric phase shifter,[21–24] and antenna[25–27] are representative. The traditional frequency agility device can be formed by the electrostrictive and magnetostrictive materials. However, these devices tend to be bulky, in slow speed of adjustment, have large energy consumption, and can only work within a narrow band. The new adjustable magnetoelectric RF/microwave devices will not only dramatically improve the design method of the military RF/microwave radio and radar, but also will greatly enhance the competitiveness of the consumer electronics industry.
According to the direction of the magnetic field and the direction of the wave vector, magnetostatic waves can be divided into magnetostatic surface waves and magnetostatic forward/backward volume waves. Because the magnetostatic surface wave has low transmission loss and the nonreciprocal transmission characteristic on the upper and lower surfaces of the ferrite slab, and contributes to the design of nonreciprocal devices.[28] At present, there are many studies into the transmission characteristics of magnetostatic surface waves and the application of microwave devices.[29] The common nonreciprocal ferrite devices are mostly multiport, such as the isolator, the circulator and the directional coupler,[30–33] and the frequency band usually does not have the adjustability. Therefore, Wu et al.[34] firstly changed the placement angle of ferrite slab in two inverted L-shaped microstrip lines and put forward a microwave band-pass filter which has nonreciprocity and adjustability of magnetic field.
Using the magnetoelectric composite materials composed of ferrite and ferroelectric materials, magnetoelectric microwave devices which have nonreciprocity and magnetoelectric adjustability have been successfully designed. For the design of microwave devices containing ferrite or magnetoelectric materials, the electromagnetic field simulation is a kind of important mean. However, due to the introduction of functional materials, the electromagnetic field simulation is time-consuming and has low-efficiency. The lumped equivalent circuit method, which is applied for the aided analysis of the performance of microwave devices, can greatly improve the designed efficiency. Marcelli et al.[35,36] firstly proposed the equivalent circuit model of the magnetostatic wave straight edge resonator. After Tsai et al.[37] established the equivalent circuit model of the double stop-band filter which consisted of two cascaded band-stop filters. In recent years, for the reciprocal dual-tunable microwave magnetoelectric device, Zhou et al.[38–41] treated the voltage of the piezoelectric layer as a magnetic field and established the lumped circuit models of the direct conduction band, the coupled band and T-type magnetoelectric microwave devices, which greatly promoted the application of the equivalent circuit model. However, the above lumped equivalent circuit models focus on the reciprocal two-port devices, and the lumped equivalent circuit model of nonreciprocal frequency band tunable microwave devices is not correlatively researched.
In this paper, considering transmission characteristics of magnetostatic waves of the filter, the lumped equivalent circuit model of a nonreciprocal magnetoelectric tunable band-pass filter is established, which is consisted of the reciprocal coupled band circuit and the nonreciprocal T-shaped circuit. The comparison of the predicted results and the experimental results of S parameters in the reciprocal and nonreciprocal cases confirms the validity of the established lumped equivalent circuit model. Then, the electric tunable performance of the magnetoelectric tunable filter, the impact of the thickness of ferrite slab and the width of the coupled microstrip line on devices are separately predicted by the lumped equivalent circuit model. It is found that these key parameters have a very significant effect on the band-pass center frequency, bandwidth, and the isolation, so the lumped equivalent circuit model will benefit the design and application of new microwave devices which have nonreciprocity and magnetoelectric adjustability.
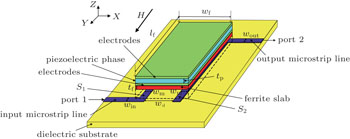
A typical reciprocal magnetoelectric (ME) tunable band-pass filter is shown in Fig.
For the nonreciprocal ME tunable band-pass filter, when the external magnetic field H is applied along the direction parallel to the plane of microstrip lines (i.e., the y direction in Fig.
According to the electrically tunable FMR frequency shifting model established by Zhou et al.,[13] a concise expression of the coefficient A is written as
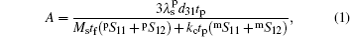
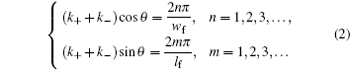
When θ = 0°, the magnetostatic surface wave is induced in the ferrite slab and transmits along the lower surface of ferrite slab. The magnetostatic surface wave is reflected on the other straight edge of the ferrite slab and transmits along the upper surface of the ferrite slab. Then the upper surface wave and lower surface wave form a circular wave. Meanwhile, due to the coupling effect between the magnetostatic surface wave and microstrip line S2, the magnetostatic surface wave is translated into the electromagnetic wave, transmits on the microstrip line and the output microstrip line, and then is outputted through the output port. When θ = 0° in Eq. (

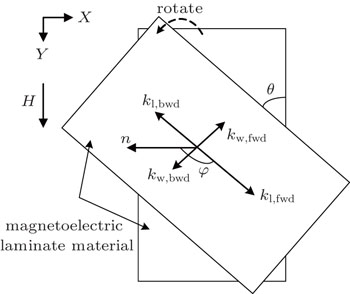
The transmission characteristic of the magnetostatic wave mainly depends on the mode of wave. The transmission characteristic is related with the included angle φ between the normal vector
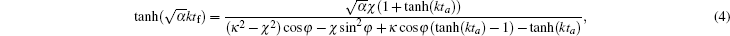
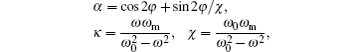
The nonreciprocal ME tunable filter is shown in Figs.
For the reciprocal coupling circuit, the radiation impedance per unit length is introduced to indicate the interaction between the magnetostatic wave and the electromagnetic wave according to the interaction principle between the magnetostatic wave and the electric current. Therefore, the radiation impedance per unit length[34] is written as
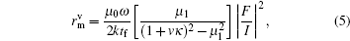
For the effective length of the microstrip line covered by ferrite slab, the total radiation impedance is calculated by the unit element integration principle and is written as

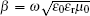
After the radiation impedance is obtained, and RLC series resonant circuit, which contains the radiation inductance L and the radiation capacitance C, is introduced to indicate the inside FMR effect of the ferrite. The unloaded quality factor Q0 = f0/(γΔH) is obtained by the resonance line width ΔH, and then the radiation impedance and the radiation capacitance are got by the definition of the unloaded quality factor of the series resonant circuit. But Marcelli et al.[35] pointed out that the coupling effect between microstrip lines and the laminated ME composites is necessarily considered to get the effective radiation inductance and radiation capacitance when the ferrite layer is located in the middle of two microstrip lines. Therefore, the coupling factor k1 = (2/Qext)exp(−kD) is introduced to describe the coupling effect between microstrip lines and the laminated ME composites, where D is the distance between the ferrite layer and the current flowing on the microstrip line; Qext is the external quality factor[36] and is written as
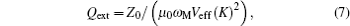
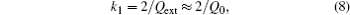
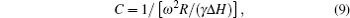
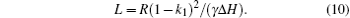
Meanwhile, the coupling inductances L1 and L2 are used to describe the coupling effect between microstrip lines and ferrite slab in Fig.
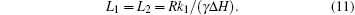
Therefore, the lumped equivalent circuit is established for the reciprocal ME device on the left side of the dashed line of Fig.
For the nonreciprocal lumped circuit shown on the right side of the dashed line of Fig.
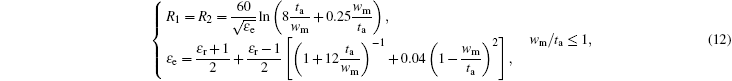
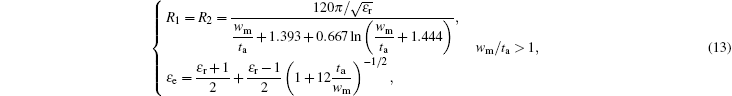
When the deviation angle θ is zero, the upper and lower magnetostatic surface waves circularly transmit and the device is reciprocal. When the deviation angle θ is non-zero, magnetostatic backward volume waves are generated due to the reflection action of the hypotenuse. Nevertheless, the magnetostatic backward volume wave cannot be returned, so the nonreciprocal characteristic is generated. Therefore, the radiation impedance R3 of the lumped equivalent circuit is the impedance of magnetostatic backward volume waves transmitting on the ferrite slab. According to the direction shown in Fig. 

The gain G of the nonreciprocal unit in Fig.
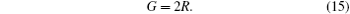
Equations (
In order to verify the validity of the lumped equivalent circuit model, the experimental results of the magnetic tunable microwave filter in Ref. [34] were selected as the reference. Wherein the YIG slab is selected as the ferrite material, the dimension lf × wf × tf is 3.6 mm × 2 mm × 0.108 mm, and the saturation magnetization is 4πMs = 1750 G. The widths of the input and output microstrip lines are win = wout = 0.37 mm, the width of the coupled microstrip line is wm = 0.32 mm, the distance between the microstrip line S1 and microstrip line S2 is wd = 1.2 mm, and the deviation angle is 45°. Here, the length of the microstrip line covered by YIG slab is about 2.5 mm, the dielectric substrate is Rogers TMM 10i, the thickness is 0.381 mm, the dielectric constant is εr = 9.8, and the loss angle tangent is tan δ = 0.002. For the nonreciprocal magnetic tunable microwave filter, the electric field is only taken as 0 in the expression of the effective magnetic field H0 of the lumped equivalent circuit model, which is shown in Fig.
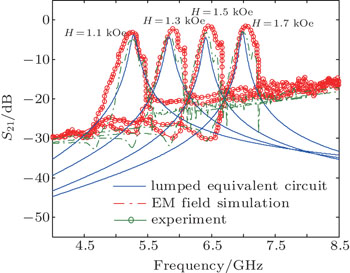 | Fig. 4. The contrast diagram of the predicted insertion loss curves of the lumped equivalent circuit model and the experiment values for the deviation angle 45°. |
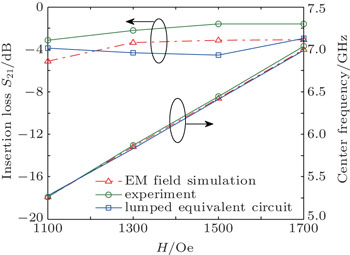 | Fig. 5. The contrast diagram of the predicted insertion loss S21 and the predicted center frequency and the experiment values under different magnetic fields. |
Meanwhile, the insertion loss S12 predicted by the equivalent circuit model is compared with the experimental results in Fig.
 | Fig. 6. The contrast diagram of the predicted insertion loss S12 of the lumped equivalent circuit model and the experiment values for the deviation angle 45°. |
Keep the thickness tf = 0.108 mm of YIG unchanged, adjust the deviation angle of YIG to be 0°. Then magnetostatic upper surface waves will not be suppressed and this filter will present the reciprocal characteristics from the above analysis. Exploiting the experimental results[34] in the reciprocal case, the comparison results of the S21 curve and the S12 curve obtained by the lumped equivalent circuit model and the experimental results are respectively shown in Figs.
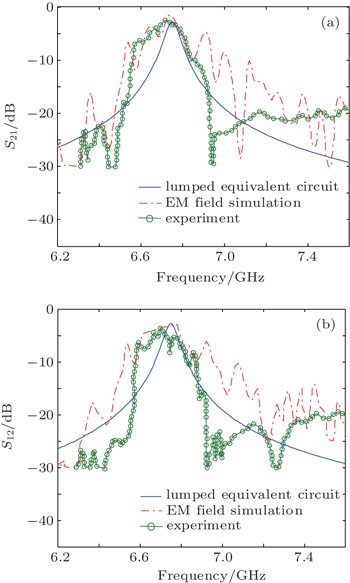 | Fig. 7. The contrast diagram of the predicted insertion loss S21 (a) and S12 (b) of the lumped equivalent circuit model and the experiment values for the deviation angle 0°. |
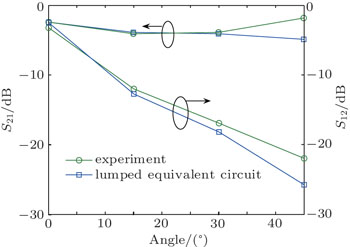
For the validity of the equivalent circuit model at the different deviation angles of ferrite slab, the experimental results in Ref. [34] are still selected. Select the 0.5 mm thick YIG slab and change the included angle between the YIG slab and the y axis to do the prediction by the model. Keeping the bias magnetic field H = 1600 Oe unchanged, the impact of the reflecting hypotenuse on the backward surface wave and the S parameter gradually increases when the deviation angle changes from 0° to 45°. As shown in Fig.
An equivalent magnetic field is introduced to describe the applied electric field on the piezoelectric layer adjusting the frequency band of devices, and then the lumped parameters of the lumped equivalent circuit model are calculated under the condition of the applied voltage. Choose PZT as the piezoelectric layer, substitute the material parameters into the magnetoelectric conversion coefficient in Ref. [13], and then get the magnetoelectric conversion coefficient A = 5.2 Oe·cm·kV−1 (i.e., the applied electric field can be equivalent to δHE = 5.2E). After the external bias field 1600 Oe remains unchanged, figure
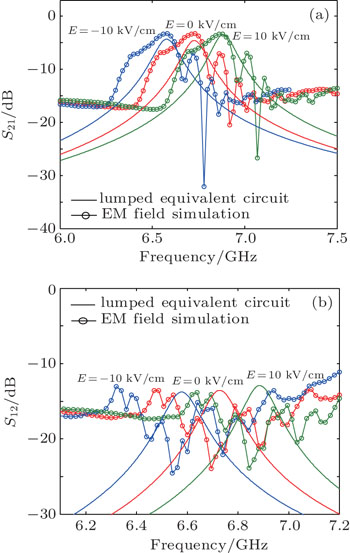 | Fig. 9. The insertion loss S21 (a) and S12 (b) curves under different electric fields (for the deviation angle 45°). |
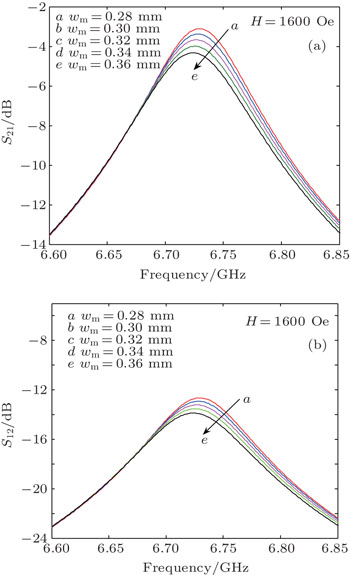
Next, the designed nonreciprocal device has several important parameters, such as the thickness of ferrite layer and the width of the coupled microstrip lines, and the impact of several important parameters on the performance of the device is predicted. Firstly, considering the impact of the thickness of ferrite layer, keep static magnetic field H = 1600 Oe unchanged, and the thickness of YIG slab changes from 0.008 mm to 0.5 mm. The insertion loss S21 and S12 curves predicted by the lumped equivalent circuit model are shown in Fig.
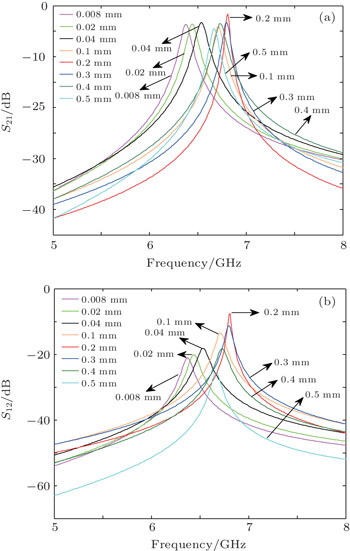 | Fig. 10. The insertion loss S21 (a) and S12 (b) curves under different thicknesses of YIG (for the deviation angle 45°). |
The insertion loss curves predicted by the equivalent circuit model are shown in Fig.
In this paper, for the nonreciprocal magnetoelectric dual tunable microwave band-pass filter, a lumped equivalent circuit model is established, which is based on the lumped equivalent circuit of the reciprocal coupled band-pass filter and the introduced nonreciprocal circuit with the controlled sources. Change the deviation angle of YIG slab to make the device respectively be in the reciprocal and nonreciprocal case. For the S21 curve predicted by the equivalent circuit model, its band-pass frequency, bandwidth, and the insertion loss are in good agreement with the experimental results. The predicted and measured insertion loss S12 results are below −15 dB under the nonreciprocal state, which have a higher isolation degree. Then, based on some important parameters of the nonreciprocal device, the lumped circuit model is used to do the prediction. It is found that the thickness of the ferrite layer has a complex effect on the center frequency and the isolation degree. YIG slab with the optimal thickness may simultaneously enhance the band-pass effect and the isolation degree. The width of the coupled microstrip line monotonically impacts on the device performance and the insertion loss S21 and S12 monotonically decrease with the increase of the width of the microstrip line.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 |