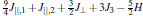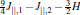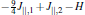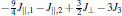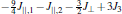† Corresponding author. E-mail:
‡ Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 11547236), the General Project of the Education Department of Liaoning Province, China (Grant No. L2015130), the Fundamental Research Funds for the Central Universities, China (Grant Nos. DC201501065 and DCPY2016014), and the Doctoral Starting-up Foundation of Dalian Nationalities University, China.
We study a mixed spin-(3/2, 1) ladder system with antiferromagnetic rung coupling and next-nearest-neighbor interaction. The exactly solved Ising-chain model is employed to investigate the ground-state properties and thermodynamics of the low-dimensional ladder system. Our results show that the competition between different exchange couplings brings in a large variety of ground states characterized by various values of normalized magnetization equal to 0, 1/5, 2/5, 3/5, 1. Moreover, an interesting double-peak structure is also detected in the thermal dependence of magnetic susceptibility and specific heat when the frustration comes into play. It is shown that the double-peak phenomenon at zero-field for the case of AF2 ground-state arises from the very strong antiferromagnetic rung coupling, while other cases are attributed to the excitations induced by temperature and external field around the phase boundary.
Low-dimensional spin systems with competing exchange interactions have received a great deal of attention in condensed matter physics.[1,2] Among various low-dimensional spin systems, frustrated magnetic ladders with different topologies of couplings offer an intriguing example to study exotic and complex phenomena such as high-temperature superconductivity, quantum phase transition, thermal conductivity, and many other interesting properties.[3–6] Theoretical and experimental investigations have shown that the main characters of spin ladders are largely determined by the number of legs. Ladders with an even number of legs have a finite spin gap between the singlet ground state and the magnetic excited states, while ladders with an odd number of legs exhibit a gapless spectrum and behave as single chains.[7]
However, most of the previous studies were focused on the ladder systems with uniform spin as the synthesized spin-ladder materials of that period basically contained one type of transition-metal magnetic ion.[8–10] In recent years, molecular magnets of ladder topology with mixed-spin structure have been experimentally realized, such as bimetallic compounds MnCu(PbaOH)(H2O)3 (pbaOH=2-hydroxy-1,3-propylenebisoxamato), MnCu(pba)(H2O)3·2H2O, and NiCu(pba)(D2O)3·2D2O (pba = 1,3-propylenebis),[11,12] motivating the related theoretical work to be carried out. The two-leg mixed spin-(1,1/2) ladder is one of the most studied systems due to the simplicity of mixture and experimental realization in several compounds. The calculated results have indicated that an interplay between frustration and spin alternation can produce both classical and quantum ferrimagnetic orders in this system, as well as interesting magnetization-plateau behaviors.[13–15] A generic quantum Heisenberg spin model is usually used to explain these exotic findings, though this model proves to be very useful, it cannot be rigorously solved due to mathematical complexities caused by non-commutability of spin operators. Therefore, various approximation methods including spin-wave series, density-matrix renormalization group, and transfer-matrix renormalization group are adopted to study the thermodynamics and magnetism. Owing to this fact, a simplified version of the quantum Heisenberg model in which the spins are partially or completely replaced by the Ising-type ones is introduced.[16] It has been demonstrated that this simple Ising model is not only exactly soluble, but also displays good correspondence to the pure quantum model under certain conditions.[17–19] In this work, we will employ this simplified Ising-chain model to study the mixed-spin ladder system, which is consist of a spin-3/2 chain coupled with a spin-1 chain through the rung and diagonal exchange bonds. The mixed-spin structure of the two-leg ladder is illustrated in Fig.
The Hamiltonian of the exactly solved ladder model reads
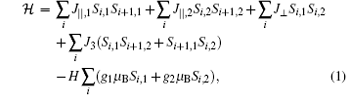
For convenience, the total Hamiltonian can be rewritten as a sum of block Hamiltonians 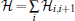
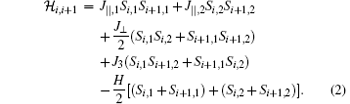
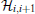
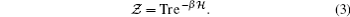
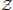
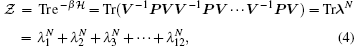
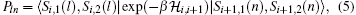
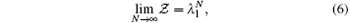
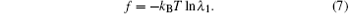
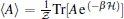
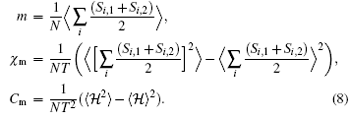
With further application of the transfer-matrix method, the final analytical expression for the average magnetization is obtained as
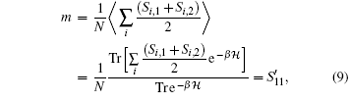
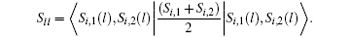
In the same way, we can obtain the final expressions of average magnetic susceptibility and magnetic specific heat as follows:
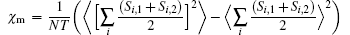
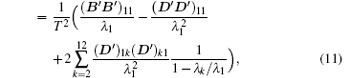

In what follows, we focus our attention on a particular case with all antiferromagnetic interactions J‖,1 >0, J‖,2 >0, J⊥ > 0, and J3 > 0, which yields the most interesting results for the mixed-spin ladder system. J3 is introduced as a reduced unit for brevity, and then we have j‖,1 = J‖,1/J3, j‖,2 = j‖,2/J3, j⊥ = J⊥/J3, h = H/J3. In Fig.
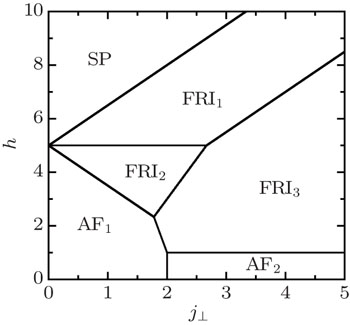 | Fig. 2. Ground-state phase diagram in the j⊥–h plane for antiferromagnetic coupling J‖,1 = j‖,2 = 1.0. |
| Table 1. Ground states of the system and their energies per block. . |
The diverse zero-temperature spin configuration observed in the phase diagram implies the multiple magnetization plateaus phenomenon and interesting thermodynamic properties. To verify the various indicative fractional plateaus, we perform a detailed examination of the magnetization process. In Fig.
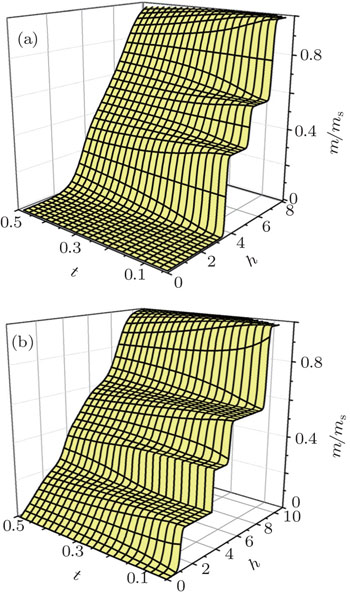 | Fig. 3. 3D plot of the normalized magnetization against temperature and magnetic field for two representative rung couplings (a) J⊥ = 1.0 and (b) J⊥ = 2.2 under J‖,1 = j‖,2 = 1.0. |
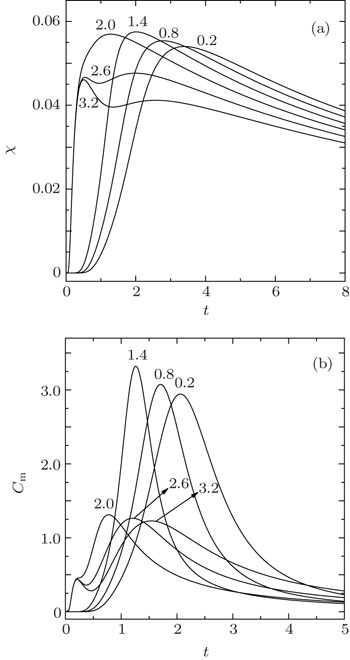 | Fig. 4. Temperature dependence of (a) zero-field magnetic susceptibility and (b) zero-field specific heat under J‖,1 = j‖,2 = 1.0 for j⊥ varying from 0.2 to 3.2. |
The thermodynamic behaviors of the typical response functions can reveal the competition between ground states AF1 and AF2 presented at zero-field. In Fig.
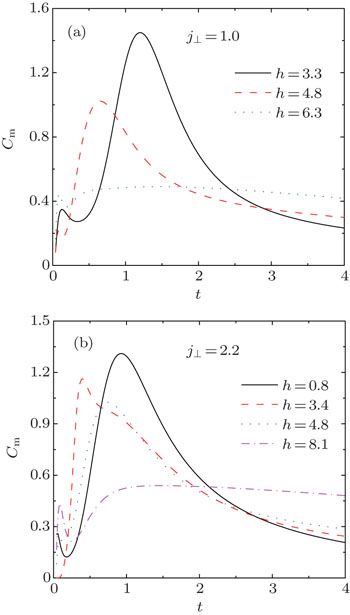 | Fig. 5. Temperature dependence of specific heat for typical rung couplings (a) J⊥ = 1.0 and (b) J⊥ = 2.2 under several different magnetic fields. |
To provide a complete profile of the thermodynamics, in Fig.
The two-leg mixed spin-(3/2, 1) ladder with frustrated rung coupling and next-nearest-neighbor interaction has been investigated in detail in this paper. The transfer-matrix method is employed to obtain the exact solutions of the basic thermodynamic quantities for the simplified version Ising-chain model. Based on the analytical results, we particularly examine the ground state, magnetization process, thermal variations of magnetic susceptibility and specific heat. Six different spin configurations can be identified in the phase diagram under the interplay between the external field and frustrated interactions. Meanwhile, the multiple plateau behavior is also evidently detected in the magnetization plots, showing an excellent coincidence with the information provided by the phase diagram. Furthermore, we also discuss the impacts of frustrated rung coupling and external field on the thermodynamic properties of this exactly solved model. It is shown that strong rung coupling will bring in an additional low-temperature peak in the zero-field magnetic susceptibility and specific heat curves. The application of external field will generate a complex variation on the double-peak structure of specific heat, implying the inherent property of different zero-temperature phase transitions.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 |