† Corresponding author. E-mail:
Project supported by the National Basic Research Program of China (Grant No. 2011CB921803), the National Natural Science Foundation of China (Grant No. 11574051), the Natural Science Foundation of Shanghai, China (Grant No. 14ZR1403400), and Fudan High-end Computing Center, China.
Under a strong magnetic field, the quantum Hall (QH) effect can be observed in two-dimensional electronic gas systems. If the quantized Hall conductivity is acquired in a system without the need of an external magnetic field, then it will give rise to a new quantum state, the quantum anomalous Hall (QAH) state. The QAH state is a novel quantum state that is insulating in the bulk but exhibits unique conducting edge states topologically protected from backscattering and holds great potential for applications in low-power-consumption electronics. The realization of the QAH effect in real materials is of great significance. In this paper, we systematically review the theoretical proposals that have been brought forward to realize the QAH effect in various real material systems or structures, including magnetically doped topological insulators, graphene-based systems, silicene-based systems, two-dimensional organometallic frameworks, quantum wells, and functionalized Sb(111) monolayers, etc. Our paper can help our readers to quickly grasp the recent developments in this field.
Topological states are insulating in the bulk but exhibit robust conducting boundary states topologically protected from backscattering. Recently, finding these topologically nontrivial states in realistic material systems has become one of the fastest developing research directions in condensed matter physics and materials science.[1–6] In a two-dimensional (2D) electron gas, quantum Hall (QH) effect,[7] which was later called the first category of the topological states, can be observed by applying an external strong magnetic field to the system, breaking the time reversal symmetry (TRS) of the system. Actually, internal magnetization can also break the TRS of a system without the need of an external magnetic field. When coupled with special band structures and spin–orbit coupling (SOC) of the system, it can generate the so called quantum anomalous Hall (QAH) effect, which was first proposed by Haldane.[8] The realization of QAH effects in realistic material systems may greatly promote the development of low-power-consumption electronics. So far, a number of theoretical proposals have been raised to produce the QAH effect,[9–34] such as mercury-based quantum walls,[9] thin films of magnetically doped topological insulators (TIs),[11] graphene and silicene based systems,[12–21] organic TIs,[22] (111) bilayers of LaCoO3,[25] and so on. The topology of a QAH state is characterized by the appearance of a quantized Hall conductivity in the absence of an external magnetic field.
To acquire QAH insulators, the following four conditions should be satisfied simultaneously: 2D systems, insulators, long-range ferromagnetic (FM) order, and special band structures with finite Chern number. In general, one real material may solely satisfy one or two of the above conditions. In particular, the insulators in nature usually have the antiferromagnetic (AFM) order instead of the FM order. Thus, real materials need to be designed and reconstructed to present the QAH effect. The finite Chern number is usually triggered by SOC interactions in the system. Forming an FM order in a 2D insulating film through magnetic doping is a classical route to produce the QAH effect. For example, the experimental realization of the QAH effect was reported in thin films of Cr- or V-doped (Bi,Sb)2Te3 topological insulators.[35–38] Actually, both the experimental and theoretical researches indicate that introducing a long-range FM order in insulating films is one of the toughest tasks in carrying out experiments with the QAH effect. Some theoretical studies have shown that the TRS of the 2D systems can be broken by introducing a magnetic exchange field through doping (adsorbing) transition-metal (TM) atoms[11,12] or proximity coupling to an FM or AFM insulator.[16–18]
In this paper, we systematically review the theoretical proposals that have been brought forward to produce the QAH effect in realistic material systems. In Section 2, we review the work of realizing the QAH effect by doping TM atoms in topological insulators. In Section 3, we introduce the theoretical model of realizing the QAH effect in graphene, and review the work of achieving the QAH effect in graphene-based systems. Silicene is a monolayer of silicon atoms with a buckled honeycomb structure but which still possesses the Dirac electronic properties, like graphene. How to realize the QAH effect in silicene-based systems is given in Section 4. In Section 5, we review the QAH effect studied in several other systems, including 2D organic topological insulators and square or triangular lattice systems, etc. In Section 6, we briefly introduce some new topological states proposed based on the QAH effect, including valley-polarized quantum anomalous Hall (VP-QAH) state and quantum spin-quantum anomalous Hall (QSQAH) state. Our conclusions and outlook are given in Section 7.
The QAH effect may be realized in a topological insulator film with quantum spin Hall (QSH) effect by breaking its TRS. If one spin state in the system is in the inverted regime and the other spin state is in the normal regime, then the inverted spin state may give a topologically nontrivial insulating state with a quantized Hall conductivity and the system will become a QAH effect insulator, indicating the QAH state closely related to the QSH state. The theoretical models and first-principles calculations showed that the QAH state can indeed be realized in the TRS-breaking topological insulator films by doping magnetic atoms.[9–11] Some typical examples are illustrated in the following.
The HgTe quantum well (QW) is a well-known QSH effect insulator,[39] which has been observed in experiments.[40] Liu et al. proposed that the QAH effect can be observed in the TRS-breaking HgTe QWs.[9] To obtain the QAH effect, the system must satisfy two conditions: (i) the state with one kind of spin is in the inverted regime while the other is in the normal regime, (ii) the entire system is still in the insulating state with a bulk band gap. The above conditions are illustrated in Fig.
 | Fig. 1. Evolution of band structure and edge states upon increasing the spin splitting. (a) The spin-down states |E1, −⟩ and |H1, −⟩ in the same block of the Hamiltonian (Eq. ( |
The tetradymite semiconductors Bi2Te3, Bi2Se3, and Sb2Te3 are also a well-known class of topological insulators.[41] Yu et al. predicted that thin films made out of this family of compounds doped with proper magnetic atoms (Cr or Fe) supported the QAH state.[11] The physical mechanism of realizing the QAH effect in the thin-film topological insulator systems with FM ordering is illustrated in Fig.
 | Fig. 2. Evolution of the sub-band structure upon increasing the exchange field. The solid lines denote the sub-bands that have even parity at Γ point, and the dashed lines denote the sub-bands with odd parity at Γ point. The blue (red) color denotes the spin-down (spin-up) electrons. (a) The initial sub-bands are not inverted. When the exchange field is strong enough, a pair of inverted sub-bands appear (red dashed line and blue solid line). (b) The initial sub-bands are already inverted. The exchange field releases the band inversion in one pair of sub-bands (red solid line and blue dashed line) and increases the band inversion in the other pair (red dashed line and blue solid line). Reprinted with permission from Ref. [11]. Copyright 2010 by the American Association for the Advancement Science. |
Graphene, which is a fascinating 2D material with a honeycomb lattice, special Dirac-cone electronic properties, and relatively mature technologies of sample growth and device fabrication, has become a prototype material for engineering the QAH effect.[12–18] Theoretical studies show that a nontrivial QAH band gap in graphene-based systems can be opened near the Dirac points in the presence of both Rashba spin–orbit coupling and magnetic exchange field.[12,13] We now introduce the physical mechanism of the gap opening and the QAH effect in graphene through the tight-binding (TB) model.[12] The TB Hamiltonian for graphene with the consideration of Rashba SOC and magnetic exchange field can be written as[12]
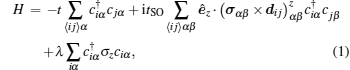
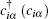
 | Fig. 3. Evolution of band structures of bulk graphene along the profile of ky = 0. The arrows represent the spin directions. (a) Pristine graphene: spin-up and spin-down states are degenerate; (b) when only exchange field λ = 0.4 is applied, the spin-up/spin-down bands are upward/downward lifted with the four bands crossing near K and K′ points; (c) when only Rashba SOC tSO = 0.1 is present, the spin-up and spin-down states are mixed around the band crossing points; (d) when both exchange field λ = 0.4 and Rashba SOC tSO = 0.1 are present, a bulk gap is opened and all four bands become nondegenerate. Reprinted with permission from Ref. [12]. Copyright 2010 by the American Physical Society. |
Figure

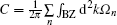
The above band evolution clearly shows the physical mechanism of realizing the QAH effect in the graphene system, indicating that graphene is an ideal system for applications of the QAH effect. In consideration of the fact that graphene has extremely weak intrinsic SOC,[45,46] both the magnetic exchange field and the SOC should be induced externally to realize the QAH effect in graphene. We now introduce the theoretical proposals of achieving the QAH effect in the graphene-based systems through adsorbing TM atoms[12,14] and proximity coupling to magnetic insulators.[16–18]
To realize the QAH effect in the graphene system, the time-reversal symmetry must be broken and the Rashba SOC must be enlarged.[12] The time-reversal symmetry of graphene can be broken by introducing an external magnetic exchange field through adsorbing TM atoms.[12–14] Besides, when adsorbing low-concentration TM atoms on the graphene sheet, the interaction between the magnetic adatoms and the π orbital of graphene, occurring on one side of graphene, will induce a sizeable Rashba SOC.[47] The first-principles calculations show that the QAH effect can be realized in graphene via adsorbing appropriate TM atoms at the hollow adsorption sites of the graphene supercell.[14] We take the case of Fe adsorbed at the hollow adsorption site of the 4 × 4 supercell of graphene as an example to illustrate the above proposal.[12] Figure
 | Fig. 4. (a) Typical structure geometry of a Fe atom on top of the hollow position of a 4 × 4 supercell of graphene. (b) Bulk band structure with SOC included along the high symmetry lines. The Fermi level is exactly located in the gap. (c) and (d) Zoom-in plots of the band structure at K and K′ points, respectively. Gaps of ∼5.5 meV, circled by the green dotted curves, are opened. (e) and (f) Berry curvature distribution Ω of the valence bands near K and K′ points. The Berry curvatures at K and K′ share the same sign, thus giving a nonzero Chern number. Reprinted with permission from Ref. [12]. Copyright 2010 by the American Physical Society. |
The above theoretical proposal shows that the QAH effect can be realized in graphene by depositing low-concentration TM atoms. The adsorption energies of the TM atoms on graphene are, however, usually very small.[14] Thus, the TM atoms tend to gather into clusters[48,49] and the long-range FM order may not survive as expected, which make it particular difficult to realize the QAH effect in TM atoms decorated graphene systems in experiments. Besides depositing TM atoms, the ferromagnetism can also be induced by proximity coupling graphene to an FM insulator, which may overcome the above mentioned problems. Depositing graphene on a magnetic substrate can induce both the magnetic exchange field and considerable Rashba SOC, essential for the realization of the QAH effect. BiFeO3 has a perovskite structure and is a G-type antiferromagnet. When graphene is deposited on the (111) surface of BiFeO3 with Fe terminal (Fig.
 | Fig. 5. (a) Supercell for graphene on a (111) BiFeO3 surface. Gray (the top layer), purple (large), yellow (medium), and red (small) colors represent C, Bi, Fe, and O atoms, respectively. (b) A top view of graphene with one layer of iron atoms. One Fe atom is located at the hollow site labeled by H, while the other two Fe atoms are located at the top sites labeled by A and B. (c) Band structure along high symmetry lines for a 4 × 4 supercell of graphene. Reprinted with permission from Ref. [16]. Copyright 2014 by the American Physical Society. |
RbMnCl3 is an AFM insulator with the Mn sites forming alternating (001) FM planes, and it also has a hexagonal structure[50] as the graphene does, which makes the experimental fabrication of the heterostructure of graphene on the (001) surface of RbMnCl3 easy. Based on first-principles calculations, Zhang et al. showed that the QAH effect could be realized in the heterostructure of graphene on the AFM insulator RbMnCl3 with Mn terminal.[17]
 | Fig. 6. Bulk band structures of graphene on BiFeO3. (a) Spin-resolved band structures. (b) Zoom in on the green box of panel (a). The blue (thin) and red (thick) lines in panels (a) and (b) represent the spin-up and spin-down bands, respectively. (c) Band structure when the spin–orbit coupling is included. A bulk gap δ of about 1.1 meV is centered on the avoided crossings near the K and K′ valleys. Note that the nontrivial band gap δ is inside the bulk gap Δ of BiFeO3. (d) Zoom in on the green box of panel (c). Reprinted with permission from Ref. [16]. Copyright 2014 by the American Physical Society. |
 | Fig. 7. (a) Side view of the heterostructure with graphene on a (001) RbMnCl3 surface. The C, Rb, Mn, and Cl atoms are denoted in brown, purple, red, and green, respectively. (b) Top view of the heterostructure with the topmost layer Mn atoms of the MnRbCl3 located at the hollow site of graphene. For clarity, only graphene and the topmost layer Mn atoms are displayed. (c) The reciprocal momentum space structures for the 1 × 1 and 3 × 3 supercells of graphene, where  |
In their first-principles calculations, a 3 × 3 supercell of graphene was employed to match the (001) surface of RbMnCl3 with Mn terminal, as shown in Fig.
 | Fig. 8. (a) The band structure (black solid curves) and the Berry curvature (red dotted curve) of the graphene/RbMnCl3 heterostructure. (b) The 2D distribution of the Berry curvature in the momentum space, located primarily around the Γ point. (c) The bulk band structure of the graphene/RbMnCl3 heterostructure with an extra hole in the supercell. (d) The bulk band gap Eg as a function of (d0 − d)/d0, where d is the distance between graphene and the RbMnCl3 film and d0 is the corresponding optimized distance. Reprinted with permission from Ref. [17]. Copyright 2015 by Nature Publication Group. |
As discussed above, the QAH effect can emerge in graphene by depositing it onto a suitable magnetic substrate. The hidden challenge in such proposals is, however, that the QAH effect depends quite sensitively on the combination configuration of graphene and the substrate. The QAH effect may be quenched if the pattern between graphene and the substrate is varied slightly, making the experimental observation very difficult. A recent first-principles study of graphene on a layered FM insulator Cr2Ge2Te6 has solved this problem.[18] The system of graphene on a Cr2Ge2Te6 film belongs to a special structure, called van der Waals (vdW) heterostructures,[51,52] due to the vdW interaction between the graphene and the substrate. This category of heterostructures is found to own several fantastic characteristics beneficial to realizing the QAH effect in experiments.
Cr2Ge2Te6 is an FM insulator with a relatively high Curie temperature of 61 K.[53] The hexagonal structure of Cr2Ge2Te6 matches very well with that of graphene. Particularly, the Cr2Ge2Te6 bulk is layered with the adjacent planes joined by vdW bonds. The Cr2Ge2Te6 films of very high quality have been successfully fabricated in experiments.[54,55] When the graphene is deposited on the 2D exfoliated film of Cr2Ge2Te6, a vdW heterostructure is formed.[51] The exotic feature of this system is that the achieved QAH effect is independent of the stacking patterns between graphene and the FM substrate. This robustness makes the experimental observation highly accessible. The Fermi level (EF) is found to be located exactly inside the nontrivial bulk band gap, favorable to the transport measurement of the QAH effect. The nontrivial bulk band gap can be tuned flexibly by varying the vdW gap between graphene and the substrate.
 | Fig. 9. Top (a) and side (b) views of one of the vdW heterostructures of graphene on a monolayer Cr2Ge2Te6. In the unit cell, two C atoms of graphene lie directly above two Te atoms (labeled by dashed circles) of Cr2Ge2Te6. Reprinted with permission from Ref. [18]. Copyright 2015 by the American Physical Society. |
Figure
 | Fig. 10. (a), (c) The calculated band structures of the vdW heterostructure in Fig. |
 | Fig. 11. (a) The calculated Berry curvature (red) for the whole valence bands. The black curves and green dots denote the band structures obtained from the DFT calculations and the TB model, respectively. (b) The calculated edge density of states for the armchair edge of the semi-infinite system. (c) and (d) The same as panels (a) and (b) except that the distance (vdW gap) between graphene and the Cr2Ge2Te6 sheet is reduced by 0.3 Å (d = 3.26 Å). (e) The induced exchange splitting (M) in the graphene layer as a function of d − d0, where d is the vdW distance between graphene and the Cr2Ge2Te6 sheet and d0 is the corresponding optimized vdW distance (d0 = 3.56 Å). (f) The SOC induced band gap Eg as a function of d − d0. Reprinted with permission from Ref. [18]. Copyright 2015 by the American Physical Society. |
The proximity coupling effect in the vdW heterostructure can be enhanced by reducing the distance between graphene and the substrate. Due to the weak vdW interaction, the distance between graphene and the FM substrate Cr2Ge2Te6 can be easily reduced in experiments by applying an external pressure. Figures
Silicene, a monolayer of silicon atoms with a two-dimensional honeycomb lattice, is closely analogous to graphene and has been synthesized in experiments.[56,57] Silicene also possesses the Dirac electronic properties and is predicted to be a 2D topological insulator (QSH insulator).[58] In contrast to graphene, silicene is in a low buckled honeycomb structure with the two sublattices in different planes, which leads to the relatively large SOC gap of 1.55 meV.[58] Similar to graphene, the QAH effect can also be realized in silicene through introducing magnetism and Rashba SOC.[19] Recent first-principles calculations demonstrated that silicene decorated with proper TM atoms at the hollow adsorption site can realize the QAH effect.[20,21] The adsorption energies of the TM atoms adsorbed on silicene are much larger than those on graphene, indicating strong structural stability of silicene decorated with TM atoms and the TM atoms generally do not form into clusters when they are deposited on the silicene sheet. The mechanism of the QAH effect in silicene with TM atoms adsorbed at the hollow site can be explained by the following TB model. In this model, the TM induced exchange field, the staggered AB-sublattice potential, and the extrinsic Rashba SOC are only considered for the Si atoms nearest to the TM adatoms. The TB Hamiltonian can be written as[19,20]


 | Fig. 12. Band structures calculated by using TB models with silicene hopping strength t = 1.6 eV. The parameters adopted are (a) U = M = 0.0 eV; (b) U = 0.18 eV, M = 0.0 eV; and (c) U = 0.18 eV, M = 0.25. When the SOC is included, bands in panel (d) are obtained. The arrows in panel (d) represent the spin directions. Reprinted with permission from Ref. [20]. Copyright 2013 by the American Physical Society. |
The band evolution obtained from the above TB model illustrates clearly how the QAH effect can be realized in the TM atoms decorated silicene system in the present of staggered AB-sublattice potential, exchange field, and Rashba SOC. Here, we take the 4d TM Nb decorated silicene system (Nb–silicene) as an example to illustrate how the QAH effect is achieved in the real system.[20] The DFT band structure of pristine silicene without SOC is shown in Fig.
 | Fig. 13. (a) Band structures for pristine (black curves) and deformed (blue curves) silicene with a 4 × 4 supercell. In the deformed case, the Nb atoms are removed. Insets: magnified bands near the K points and the optimized structure around the Nb. (b) and (c) The band structures of silicene adsorbed with Nb without (b) and with (c) the consideration of spin polarization, respectively. The contributions from Si 3p/Nb 4d states to the bands are denoted by the orange/blue circles. The inset in panel (c) is the spatial distribution of the spin difference. (d) The corresponding bands of panel (c) with the SOC. The EF is set at energy zero. Reprinted with permission from Ref. [20]. Copyright 2013 by the American Physical Society. |
Since the adsorption energies of TM atoms on silicene are large and the TM atoms generally do not form into clusters, one may expect the realization of the QAH effect through adsorbing TM atoms on silicene is easier in experiments, compared to graphene. There are, however, other difficulties in the system. Due to the absence of the freestanding silicene in nature, the silicene is usually grown on metal substrates in experiments, which will absolutely destroy the original QAH effect. Thus, to realize the QAH effect in TM decorated silicene systems in experiments, some suitable insulating substrates must be first designed for silicene. For graphene, the freestanding monolayer exists in nature and has been fabricated successfully in experiments. According to the above discussion, the QAH effect in graphene systems can hopefully be realized in experiments by forming graphene-based heterostructures, especially the vdW-heterostructure, through depositing a graphene sheet on suitable magnetic insulating substrates.
Besides the typical systems of HgTe QWs, (Bi,Sb)2Te3 thin films, graphene (heterostructures), and silicene, etc., QAH effects have been reported in many other material systems, including 2D organic topological insulators,[22] heavy atomic layers on magnetic insulators,[23] (111) bilayers of LaCoO3,[25] GdO/EuO quantum wells,[26] interfaces between thin films of the topologically trivial FM insulators EuO and GdN,[27] (001) double-perovskite monolayers via intersite spin–orbit coupling,[28] and so on.
 | Fig. 14. (a) and (b) Band structures of the TMn lattice without and with SOC, respectively. The red (blue) dashed curves denote spin-up (spin-down) bands. (c) and (d) Magnification of panels (a) and (b) around EF, respectively. Reprinted with permission from Ref. [22]. Copyright 2013 by the American Physical Society. |
Wang et al. proposed that the QAH effect can be realized in a family of 2D organic topological insulators which are designed by assembling molecular building blocks of triphenyl-transition-metal compounds into a hexagonal lattice and using the triphenyl-manganese (TMn) as a model system with the Mn atoms forming a honeycomb lattice.[22] Figure
 | Fig. 15. (a) Top view and (b) side view of the tripled surface unit cell of MnTe with 2/3 ML Pb. Pb is in green, Mn is in gray, Te is in dark blue, and I is in cyan. Reprinted with permission from Ref. [23]. Copyright 2013 by the American Physical Society. |
A large gap QAH effect was predicted to be realized by depositing atomic layers of heavy atoms (Pt–Bi) with large SOC on the surface of magnetic insulators (such as MnTe, MnSe, and EuS) (Fig.
The QSH effect in the InAs/GaSb quantum well (QW) is due to the relative band inversion between the two different materials. Zhang et al. showed that the above relative band inversion mechanism could also be applied to oxide heterojunctions, and proposed that the QAH state could be realized in the (CdO)n(EuO)m QW (Fig.
Liang et al. demonstrated that the topological states could also be realized in a triangular lattice.[59] They found that, because of the C3 and time reversal symmetries, px and py orbitals accommodated on the triangular lattice exhibit a quadratic band touching at the Γ point at EF. When the SOC is included, a gap will be opened at the touching point, which results in a QSH effect state. Thus, if the time reversal symmetry of the triangular lattice system is broken by a large magnetic exchange field, the QAH effect with C = ±1 will be achieved.
 | Fig. 16. Structures of stanene with (a) full- and (b)–(c) half-passivation by I atoms. Large gray and small pink spheres represent the Sn and I atoms, respectively. For the half-passivated stanene, unpassivated Sn sites exhibit magnetic moments in a triangular lattice (dotted lines), which are indicated by the blue arrows. The FM and 120° AFM phases are indicated in panels (b) and (c), respectively. The spin charge density is shown in an isovalue surface plot, which distributes primarily at the unpassivated Sn atoms. The isovalue of the spin density is chosen as 0.006 electron/Å3. Reprinted with permission from Ref. [24]. Copyright 2014 by the American Physical Society. |
 | Fig. 17. (a) The rocksalt crystal structure of CdO and EuO with space group  |
 | Fig. 18. Schematic densities of states of (a) EuO and (b) GdN. (c) Side view of the proposed interface structure composed of one GdN layer atop one EuO layer on a SrO substrate. Large atoms are cations (Gd, Eu, and Sr), and small atoms are anions (N and O). Reprinted with permission from Ref. [27]. Copyright 2014 by the American Physical Society. |
The valley-polarized quantum anomalous Hall state and the quantum spin-quantum anomalous Hall state are the QAH-related new topological states, where two different quantum states coexist in a material system. The valley degree of freedom in the honeycomb lattice system is essential for the application of valleytronics.[60] Silicene has a honeycomb geometry and a low-buckled structure. By breaking the inversion symmetry of silicene, e.g., by introducing a relatively large staggered AB-sublattice potential, a bulk band gap can be opened at the K and K′ points and the quantum valley Hall (QVH) effect can be obtained, characterized by the valley Chern number 

Ezawa reported from TB models that the topological properties of silicene could also be tuned by applying the staggered exchange field ΔM = MA − MB, where MA and MB are the magnetic exchange fields operating on the A and B sublattices, respectively.[63] The QSH state and the QAH state are the well-known topologically protected states, which are characterized by the helical and the chiral gapless edge states, respectively. By introducing the staggered magnetic exchange field ΔM, the author discovered a new hybrid topological state, the quantum spin-quantum anomalous Hall (QSQAH) state, where the two different topological states coexist, i.e., the QSH effect is realized at one valley (K point) while the QAH effect is realized at the other valley (K′ point).[63] The topological numbers of QSQAH are given by one half of the sum of those of the QAH and QSH states: Chern number C = ±1 and spin Chern number Cs = 1/2. Based on the first-principles calculations, Zhou et al. reported the novel QSQAH effect in the Sb(111) monolayers decorated with H and certain magnetic atoms.[64] The drastic exchange field induced by the decoration of H atoms and magnetic (Cr/Mo/W) atoms at the A and B sublattices of the honeycomb Sb(111) monolayers, together with the strong SOC of the Sb atoms, generates the novel QSQAH state.[64] Figure
 | Fig. 19. (a) Contour of Berry curvature distribution in (kx, ky) plane for the valley-polarized QAH effect. (b) Berry curvature distribution as a function of kx at fixed ky = 2π/√3. (c) The band structure of zigzag-terminated silicene exhibiting the valley-polarized QAH effect, where colors are used to label the edge modes localized at the opposite boundaries. (d) Valley-associated edge modes for the valley-polarized QAH effect. Reprinted with permission from Ref. [61]. Copyright 2014 by the American Physical Society. |
| Table 1. Summary of the material systems proposed for realizing the QAH effect. The listed contents include the material systems, the Chern numbers obtained in the systems, the important characteristics, the QAH gaps, and the corresponding references. . |
 | Fig. 20. (a) Berry curvatures (red dots) for the whole valence bands (in atomic units (a.u.)) of Mo@SbH in the case of 1 × 1 unit cell, with a 3% tensile strain applied. The corresponding band structures (black dashed curves) are also displayed. (b) The distributions of the Berry curvatures in 2D momentum space for the same system in panel (a). (c) and (d) The same as those in panels (a) and (b), respectively, except for spin Berry curvatures (blue dots in (c)) instead. (e) and (f) The same as those in panels (c) and (d), except for the case of 2 × 2 supercell. The bands in panel (e) are shown by black solid curves. In panels (e) and (f), no strain is applied. Reprinted with permission from Ref. [64]. Copyright 2015 by the American Chemical Society. |
The material systems proposed for realizing the QAH effect have been summarized in Table
In this review, we systematically discussed the theoretical proposals for realizing the QAH effect in various real material systems. The theoretical studies demonstrate that the QAH effect can be realized in the TRS broken QSH insulator HgTe QWs and tetradymite semiconductors Bi2Te3, Bi2Se3, and Sb2Te3 by doping magnetic atoms. By introducing Rashba SOC and a magnetic exchange field, graphene and silicene are suitable prototype materials for engineering the QAH effect. The QAH effect can also be realized in various other real materials, such as 2D organic topological insulators, heavy atomic layers on magnetic insulators, GdO/EuO quantum wells, (111) bilayers of LaCoO3, and so on. Two QAH-based novel topological states, VP-QAH state and QSQAH state, were also discussed in this work. Although there are plenty of theoretical proposals, the QAH effect has solely been observed in experiments in thin films of magnetically doped topological insulators ((Bi, Sb)2Te3) at an extremely low temperature. It is generally not very easy to synthesize the proposed material systems theoretically, which makes the experimental realization of the QAH effect challenging. Thus, to realize the QAH effect straightforward in experiments, the proposed system must be robust against disorder and easy to be synthesized, where a high TC and a relatively large bulk band gap are also required. When compared to the other materials in the theoretical proposals, graphene is the most stable 2D material and relatively mature to be fabricated in experiments, which indicates that the robust QAH effect proposed in the graphene-based vdW heterostructure may be the most perfect candidate system for experimental observation of the QAH effect up to the present. Further, to apply the QAH effect in future low-power-consumption electronic devices, the room-temperature QAH state must be achieved in certain material systems, which calls for more effort on the experimental and theoretical studies in this significant direction.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 | |
| 52 | |
| 53 | |
| 54 | |
| 55 | |
| 56 | |
| 57 | |
| 58 | |
| 59 | |
| 60 | |
| 61 | |
| 62 | |
| 63 | |
| 64 |


