The efficiency of a material directly converting thermal energy into electrical energy or vice versa can be described by the dimensionless charge figure of merit (FOM) , where S_c is the charge Seebeck coefficient (thermopower), G_c is the electric conductance, κ_el(ph) is the electric (phonon) thermal conductance, and T is the operating temperature. In bulk materials, however, the value of Z_cT remains at about one due to the restriction of the Wiedemann–Franz (W–F) law.^[1] In recent years, the study of high efficient heat-electricity conversion in low-dimensional materials has become an active subject due to the effective improvement in conversion efficiency.^[2–5] Thermoelectric effects in quantum dot (QD) systems have been widely studied both experimentally and theoretically.^[6–14] In the QD systems, the thermoelectric effects can not only lead to considerable values of Z_cT due to the strong violation of the W–F law^[8] and small phonon contribution to the thermal conductance,^[9] but also reveal many novel thermoelectric phenomena such as Coulomb blockade oscillations of the thermopower and the thermal conductance,^[11] and the bipolar effect in the thermal conductance spectrum.^[14] In the QD systems, the thermoelectric figure of merit can be largely enhanced by the Coulomb blockade effect.^[14] Moreover, experiments have demonstrated the capability of measuring the Seebeck coefficients in atomic and molecular junctions,^[15–17] which inspires the theoretical study on the thermoelectric properties of nanojunctions.^[18–24]

Recently, the spin Seebeck effect has been observed in a metallic magnet using a spin-detection technique based on the spin Hall effect,^[25] in which the temperature difference between the edges of a bulk ferromagnetic slab plays a role of the driving force for the spin voltage and spin current. This spin Seebeck effect is an analogy to the usual charge Seebeck effect, and can be applied directly to the thermal spin generators for driving spin current.^[26–28] It is more interesting that a heat flow can also been converted into a spin voltage in the magnetic insulator despite the absence of conduction electrons.^[29] Using a similar experiment geometry, one also observed the spin Seebeck effect in ferromagnetic semiconductors.^[30] The influence of the ferromagnetic leads on the thermoelectric transport properties has also been investigated in the QD systems with ferromagnetic electrodes.^[31–34] In addition, the quantum interference effects such as Fano effect, Dicke resonances, and Aharonov–Bohm oscillations have been proposed as methods of increasing the thermoelectric efficiency in the QD systems.^[35–39] Thus many efforts have been devoted to improving the thermoelectric efficiency in the QD systems. In particular, the Rashba spin–orbit interaction (RSOI) in the QD was used to produce the spin-dependent thermoelectric effect. In Refs. [34] (single QD system) and [28] (DQD system), the coexistence of the RSOI in the QD and the leads’ spin polarization enhanced the figure of merit of the spin thermoelectric effects. Reference [27] investigated the thermospin effects in parallel coupled DQD under the coaction of the Rashba spin–orbit interaction and the Zeeman splitting in the DQD, mainly involving the effect of the magnetic field applied to the DQD on the thermoelectric coefficient. However, in multi-QD systems, the research on the spin-dependent thermoelectric properties and the influence of the interference effects remains few. In this paper, we study the spin-dependent thermoelectric transport through parallel triple quantum dots (TQDs) with Rashba spin–orbit interaction (RSOI) embedded in an Aharonov–Bohm interferometer connected symmetrically to the leads, in which the coexistence of a bound state in the continuum (BIC)^[40] and a Fano resonance results in wide regions in the space of parameters of large spin thermopower. Due to the presence of the RSOI, both the magnetic flux phase and the RSOI phase affect the thermoelectric transport properties. The spin-dependent electrical and thermal conductances, the thermopower, and the figure of merit as functions of the QD energy level are calculated in the linear-response regime. Under the appropriate configuration of the magnetic flux phase and RSOI phase, the spin figure of merit can be enhanced and even is larger than the charge figure of merit. In particular, the thermopower in both the magnetic flux phase and the RSOI phase is studied when other parameters are given. We find that the device can provide a mechanism of thermal spin battery that converts the heat into a spin voltage and induces a pure spin current.

We consider a TQD molecule with RSOI coupled symmetrically to two leads (see Fig. 1). The RSOI is only in QD1 and QD3. The system can be modeled by a noninteracting Anderson Hamiltonian H = H_dot + H_lead + H_T, with the QD Hamiltonian

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. Schematic diagram of a coupled TQD system with RSOI in DQ1 and DQ3.

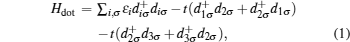
By using the nonequilibrium Green’s function technique, the electronic and heat currents flowing in the system can be written in the forms

Here and are, respectively, the retarded and the advanced Green’s functions in ω space with is defined by the matrix elements with θ(t) the step function. are matrices describing the coupling between the QDs and the leads, whose matrix elements are defined as .

In the linear response regime, the chemical potentials and the temperatures of the two leads are set to be μ_L = μ_R = μ and T_L = T_R = T. In this system, the chemical potential difference between the two leads is related to the spin channel. One can introduce a spin-dependent voltage ΔV_σ = ΔV + δ_σΔV_s with charge bias ΔV and spin bias ΔV_s. The spin bias originates from spin accumulation. Corresponding, the spin-resolved electric and heat currents can be expressed as

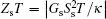
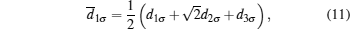
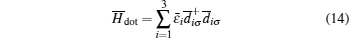
For simplicity, we take V₁ = V₃ = V and V₂ = βV with both V and β real, at the same time assume ϕ_R1 = −ϕ_R3 = Δϕ_R/2. Thus, in the new subspace these coupling coefficients can be expressed as

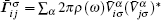
Now we investigate numerically the spin-depended thermoelectric transport through the system. For convenience, Γ = 2πρ(0)V² is used as the energy unit with ρ(0) the density of states in the leads. The system temperature T is fixed to be 0.026Γ (the constant k_B = 1). The other parameters are chosen as μ_L = μ_R = 0, t = 2Γ, and β = 1. In the presence of the RSOI and the magnetic flux, the electron transmission depends on the phase factors, which is presented in the transmission coefficient

The dependence of the transmission on the phase factor can be used to tune the thermoelectric coefficients via . According to the definition of the phase ϕ_σ, the RSOI phase is equivalent to the magnetic flux phase. However, actually, the influence of the two on the thermoelectric transport is not exactly the same. The influence of the RSOI phase is related to electron spin, which results in some interesting properties of thermoelectric transport. Figure 2 shows the thermoelectric coefficients as functions of the QD level for t = 2Γ and φ = 1.25π, Δϕ_R = 0.25π. In general, the conductance should exhibit three resonance peaks corresponding to the three molecule-state levels. However, under the configuration of the magnetic flux phase and the RSOI phase, the coexistence of BIC and Fano resonance can occur for appropriate matching of the two phases. G_↓ (κ_el↓) presents an asymmetric resonance peak near the bonding state due to the Fano resonance in transmission, and the peak at ε = 0 merges with the peak near the antibonding state , forming a wider peak, see Figs. 2(a) and 2(b). While for G_↑ (κ_el↑), BIC appears near the antibonding state and the Fano resonance does not occur near the bonding state, which leads to large spin thermopower appearing in a wide range of energy. Figures 2(c) and 2(d) show the thermopower and the figure of merit as functions of the QD level. Due to the Fano resonance in the vicinity of the bonding state, the spin-dependent thermopower S_↓ presents a relatively large value, as a result, the spin thermopower S_s also presents a relatively large value, and the spin figure of merit Z_sT is even larger than the charge figure of merit Z_cT.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. Thermoelectric coefficients (a) G, (b) κ, (c) S, and (d) ZT as functions of the QD level ε for t = 2Γ. Here the phase factors are set to be φ = 1.25π and ΔϕR = 0.25π.

In order to observe comprehensively the modulation of the configuration of the magnetic flux phase and the RSOI phase on the thermoelectric coefficients, we present the thermopower as a function of both the magnetic flux phase φ and the RSOI phase Δϕ_R in Fig. 3. It is convenient to consider the contour graphs as a function of two variables (φ,Δϕ_R) (the other parameters are ε = 0.01 and t = 2Γ). The spin-dependent thermopower S_σ presents a double-peak structure and these peaks locate at (φ,Δϕ_R) = (x, δ_σx + 4n ± 1/4), where n = 0,±1,±2,…, and x ∈ (−∞, ∞), see Figs. 3(a) and 3(b). The charge thermopower S_c and the spin thermopower S_s are made up of S_↑ and S_↓. They present a quadruple-peak structure near (φ,Δϕ_R) = (4n,4m) (n,m = 0,±1,2,…) for S_c and near (φ,Δϕ_R) = (4n + 2,4m + 2) (n,m = 0,±1,2,…) for S_s. More precisely, these peaks, as shown in Figs. 3(c) and 3(d), locate at (φ,Δϕ_R) = (4n,4m±1/4) and (4n±1/4,4m) for the charge thermopower S_c, and at (φ,Δϕ_R) = (4n + 2,4m + 2±1/4) and (4n + 2±1/4,4m + 2) for the spin thermopower S_s, which can be used to optimize the thermoelectric efficiency. One can also find from Figs. 3(c) and 3(d) that for some specific configurations of the magnetic flux phase and the RSOI phase, when S_s is close to its peak value, S_c tends to zero, meaning that a pure spin current can be obtained near these specific configurations of the phases. In order to see this more clearly, in Fig. 4, we plot the thermopower S as a function of ε for (φ,Δϕ_R) = (−1.68,−1.96) (point M in Fig. 3). For this configuration of the phase, the amplitudes of S_↑ and S_↓ are equal at ε = 0.01, but present opposite signs. As a result, S_c vanishes while S_s ≈ 1 near ε = 0.01, the corresponding figure of merit is only 0.1. Further optimizing the operating parameters, one can obtain larger S_s and corresponding Z_sT. For example, for(φ,Δϕ_R) = (1.25,0.25), S_s ≈ −1.5 and Z_sT ≈ 0.6 near ε = −3, see Figs. 2(c) and 2(d). Hereby, under appropriate matching of the parameters, the system could be considered as an effective spin battery that can convert heat into a spin voltage and induce a pure spin current in the device. Moreover, the interdot tunneling coupling t also has an obvious effect on the thermoelectric properties of the system.

Fig. 3.

	Figure Option ViewDownloadNew Window
	Fig. 3. Contour graphs of spin-dependent thermopower Sσ, charge thermopower Sc, and spin thermopower Ss as functions of the magnetic flux phase φ and the SROI phase ΔϕR for ε = 0.01Γ. The other parameters are the same as those in Fig. 2.

Fig. 4.

	Figure Option ViewDownloadNew Window
	Fig. 4. Thermopower S as a function of the QD level for phase factor φ = −1.68π and ΔϕR = −1.96π. The other parameters are the same as those in Fig. 2.

For a given configuration of the magnetic flux phase and the RSOI phase, one can obtain maximal thermopower by choosing the appropriate interdot coupling. In Fig. 5, we plot the spin thermopower S_s as a function of the interdot tunneling coupling t for the configuration of the magnetic flux phase and the RSOI phase. In the vicinity of t = 0.6 Γ, the spin thermopower reaches its maximum .

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Spin thermopower Ss as a function of t for ε = 0.01Γ. The other parameters are the same as those in Fig. 4.

We have studied the spin-dependent thermoelectric transport through a parallel triple-dot system with RSOI embedded in an Aharonov–Bohm interferometer connected symmetrically to leads using the nonequilibrium Green’s function method in the linear response regime. Because the influences of the magnetic flux phase and the RSOI phase on the thermoelectric transport are not exactly the same, the thermopower can be considered as a function of both the magnetic flux phase φ and the RSOI phase Δϕ_R when other parameters are given. The contour graphs of spin-dependent thermopower S_σ present double-peak structures in the specific (φ,Δϕ_R) region. While the charge thermopower S_c and the spin thermopower S_s present quadruple-peak structures. For some specific configurations of the magnetic flux phase and the RSOI phase, one can obtain the spin thermopower while the charge thermopower vanishes, which is useful in realizing the thermal spin battery that would allow to convert heat into a spin voltage and induce a pure spin current in the device. Moreover, under the appropriate configuration of the phase and parameters, one can obtain a relatively large spin thermopower and the spin figure of merit Z_sT is even larger than the charge figure of merit Z_cT.