† Corresponding author. E-mail:
Project supported by the National Basic Research Program of China (Grant Nos. 2013CB921901 and 2014CB239302).
The discovery of Dirac semimetal and Weyl semimetal has motivated a growing passion for investigating the unique magneto-transport properties in the topological materials. A Weyl semimetal can host Weyl fermions as its low-energy quasi-particle excitations, and therefore perform exotic features analogous to those in high-energy physics, such as the violation of the chiral charge conservation known as the chiral anomaly. One of the electrical transport signatures of the chiral anomaly is the Adler–Bell–Jackiw (ABJ) anomaly which presents as a negative magnetoresistance when the magnetic field and the current are parallel. Very recently, numerous experiments reported negative longitudinal magnetoresistance (NLMR) in topological materials, but the details of the measurement results are various. Here the materials and the corresponding experiment results are briefly reviewed. Besides the plausible explanation of the ABJ anomaly, some other origins of the NLMR are also discussed.
Magnetoresistance (MR = Δρ/ρH=0) is defined as the change of a material’s resistance in a magnetic field. The sign and magnitude of MR depend on various factors, such as the band structure of the materials, the carrier mobilities, whether the sample is mono-crystalline or polycrystalline, the directions of the magnetic field and the current, the strength of the field, and the temperature.[1] The study of MR is important not only for fundamental condensed matter physics but also for applied science and applications. Previous explorations have provided promising candidates for magnetic memory or other electronic devices, such as giant magnetoresistance (GMR) in magnetic multilayer and colossal magnetoresistance (CMR) in manganeses.[2,3] Magnetoresistance in real materials is commonly observed as positive except for several special cases. One exception is the MR in a ferromagnet, in which the polarization of the electrons and their scattering can be affected by a magnetic field and lead to a negative MR.[1] Another well-known scenario is weak localization (WL) of electrons in two-dimensional (2D) systems which falls off in the presence of a magnetic field and leads to a negative MR in a low field.[4]
Unlike in the setup of the transversal magnetoresistance (TMR) in which the magnetic field (B) is perpendicular to the electric field (E), B does not apply a Lorentz force on the electrons moving along the direction of E in the longitudinal magnetoresistance (LMR) setup. This simple argument seems to imply the absence of LMR which is however observed in many materials in experiments. A conventional metal such as copper shows a positive LMR with the magnitude about 10%,[1] while some semimetals such as graphite show large positive LMR.[5] On the other hand, negative longitudinal magnetoresistance (NLMR) is less reported for non-magnetic materials.
Recent studies on topological materials in condensed matter physics have motivated the interest on the electrical transport properties of semimetal and semiconductor in magnetic field.[7–9] Topological materials include topological insulator (TI), Dirac semimetal (DSM), and Weyl semimetal (WSM). Experimental studies on these topological materials have revealed some unique features including large TMR, high carrier mobilities, and strong Shubnikov–de Haas (SdH) oscillations. Physicists are also looking for exotic features due to the breaking of the conservation laws of classical physics by quantum mechanical effects in these topological materials. The most primitive example is the so-called chiral anomaly associated with Weyl fermions. A Weyl fermion is a massless fermion that carriers a definite chirality. In the full quantum-mechanical theory, the chiral charge of Weyl fermions is not conserved due to the chiral anomaly.[10,11] A WSM or DSM in a magnetic field can host Weyl fermions as its low-energy quasi-particle excitations.[12–14] The correspondence theory between high-energy and condensed matter physics indicates that the chiral anomaly may be observed in WSM and DSW.[15] In this situation, parallel magnetic and electric fields can pump electrons between Weyl nodes of opposite chirality that are separated in momentum space. This process violates the conservation of the chiral charge, giving rise to an analogue of the chiral anomaly in a condensed matter system (Fig.
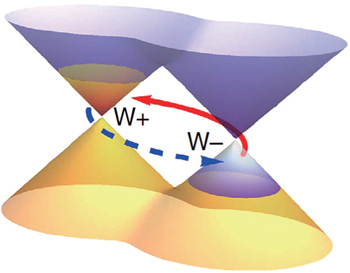 | Fig. 1. A cartoon illustrating the chiral anomaly which leads to the axial or chiral charge pumping, E·B. This causes a population imbalance difference between the Weyl cones with opposite chiralities. From Ref. [6]. |
This short review paper focuses on the experimental results of the NLMR in the topological semimetal. We have noticed that new experimental results are presented when this draft is being prepared, while the theoretical studies on the LMR for topological materials are still ongoing. We wish this short review can help readers to realize the variety and complication of the magneto-transport phenomena of the topological semimetal. For the development of the transport theory, especially for the LMR, readers can select Refs. [1], [16], and [17]. An introduction of the chiral anomaly in WSMs focusing on the theory can be found in Ref. [18]. For more informations about topological materials, readers can select Refs. [19] and [20].
Negative LMR is not a new phenomenon in semimetal. ‘Anomalous longitudinal magnetoresistance’ about −50% at 4.2 K for mono-crystalline antimony was reported in 1955 (Ref. [21]), and subsequently for bismuth in 1957 (Ref. [22]). For semiconductor n-type InSb, NLMR up to −70% at 77 K was reported.[23] Non-saturating NLMR up to at least 60 T was reported in polycrystalline Ag2Se and Ag2Te (Ref. [24]). Previous studies explained the NLMR in terms of geometry of inhomogeneous currents under the influence of the magnetic field[25] (i.e., a current jetting effect) or the ionized impurity scattering in strong magnetic field prohibiting the back-scattering.[26] The studies on the thin films of TI Bi2Se3 observed a small NLMR which is likely due to a WL effect in the presence of the magnetic field.[27]
The transport experiment by Kim et al. on Bi1−xSbx found NLMR in topological materials and connected it to the ABJ anomaly for the first time.[28] The alloy of Bi1−xSbx undergoes a topological phase transition from a band insulator to a topological insulator for x ≃ 0.03, at which concentration the alloy is identified as a DSM. When applying a magnetic field on Bi0.97Sb0.03, the Dirac nodes are split to Weyl nodes with opposite chiralities, and an electric field (E) parallel with the magnetic field (B) will induce an axial charge pumping effect. Figure
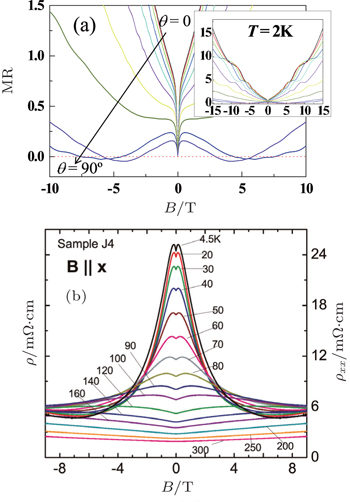 | Fig. 2. The NLMR for DSM Bi0.97Sb0.03 and Na3Bi. (a) Angle-dependent MR for Bi0.97Sb0.03. Negative MR occurs when B ‖ i. From Ref. [28]. (b) LMR for Na3Bi at selected temperatures. From Ref. [29]. |
Unlike the alloy Bi1−xSbx in which the DSM state only occurs at the topological phase transition point, the DSW Cd3As2 and Na3Bi have the nodes at zero energy protected against gap formation by crystalline symmetry.[30,31] The observations of their DSM states in angle resolved photo-emission spectroscopy (ARPES) experiments[32,33] have stimulated intense interest in the possibility of observing charge pumping effects in the Weyl states which is driven by an external magnetic field on these DSWs. Cd3As2 belongs to a group of II–V compounds and crystallizes in a body-central tetragonal structure. Different single-crystal-growth methods yield samples with distinct electrical properties. The bulk crystals of Cd3As2 from flux growth have a high carrier concentration (ne ∼ 1018 cm−3) and a metallic ρ(T) profile.[34] The samples from flux growth show giant TMR at base temperature and a weak negative term in LMR.[34] Recently, the electrical transport properties of Cd3As2 microwires and nanowires with ne ∼ 1016–1017 cm−3 were reported.[35,36] Unlike the bulk crystals, the wires grown via chemical vapor transport method have a semiconducting-like ρ(T) profile, and their TMR is smaller in general. Li Cai-Zhen et al.[35] and Li Hui et al.[36] reported a similar profile of the LMR for Cd3As2 at base temperature: it has a small dip for B < 0.2 T due to WAL and shows a negative term up to −60% for B < 6 T, and then tends to be positive in higher field. The NLMR shows an reciprocal parabolic dependence on the low field and persists up to 300 K.[35] The NLMR was ascribed to the ABJ anomaly and the system was believed to enter the quantum limit (QL) in the higher magnetic field, in which the MR becomes positive.[36] Nanoplates of Cd3As2 were reported to show NLMR below 200 K as well.[37]
The physical properties of Na3Bi are less reported than those of Cd3As2, probably because the compound is air-sensitive. Xiong et al. reported electrical transport measurements on millimeter-sized, hexagonal plates of Na3Bi single crystals.[29] The samples which have NLMR display a non-metallic ρ(T) profile with low carrier density n ≃ 1017 cm−3 at base temperature. The analysis of the SdH oscillations for B ⊥ i revealed that the cross section of the Fermi pocket is less than 5 T. The LMR falls rapidly to saturation to an almost field-independent value above 5 T, and then slightly increases with increasing field, which is likely due to a small misalignment of the field. The authors also measured the resistivity for different configurations of the current and the magnetic field which was rotated in plane, and found that the maximum of the negative MR is locked to the field and current, rather than being pinned to the crystal axis. This locking pattern in weak magnetic field in Na3Bi is believe to be the signature of the axial current.
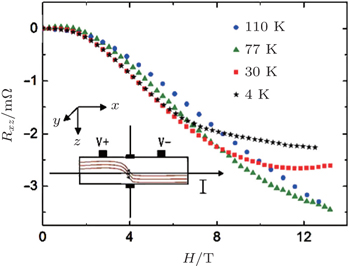
The electronic state of ZrTe5 is still under debate: it could be a TI with a very narrow bulk gap or a DSW, according to band structural calculations and experiments.[38–40] ZrTe5 crystallizes in a layered orthorhombic structure in which the layers are stacked along the b axis.[41] Single crystals of ZrTe5 synthesized in lab in general have a ribbon-like shape with a long direction along the a axis and a plate perpendicular to the b axis. ZrTe5 is well-known for its anomalous ρ(T) profile in zero field, large TMR at low temperatures, and large thermoelectric performance. Li et al. reported that the LMR of ZrTe5 shows a small cusp-like feature for B < 1.5 T and then a negative contribution which persists up to 110 K. The change of the LMC is proportional to B2, which indicates a chiral magnetic effect.[42] Recently, Wang et al. reported that the isostructrural compound HfTe5 shows a small NLMR[43] as well. The experiment by Hirschberger et al. revealed the NLMR in the half-Heusler GdPtBi which is a zero-gap semiconductor with a quadratic band dispersion but hosts Weyl nodes in a magnetic field.[44] Naumannite β-Ag2Se crystallizes in a non-central symmetric, orthorhombic structure and band structural calculations demonstrate that it can be an inversion-symmetry-breaking WSM or a narrow band gap TI.[45] The transport experiment on mono-crystalline Ag2Se showed that its LMR has SdH oscillations in low field and then negative LMR emerges beyond the QL.[46] The oscillations fade out at 40 K but the negative LMR still persists. The LMC is linearly dependent on the field beyond the QL.
Weyl semimetal is another type of topological semimetal. Weyl semimetal has pairs of non-degenerated, topologically stable band-touching Weyl nodes separated in momentum space.[14] Weyl nodes are associated with a chiral charge that protects the gapless surface states on the boundary of a bulk sample. These surface states take the form of Fermi arcs connecting the projection of bulk Weyl nodes in the surface Brillouin zone. The Weyl fermions in the bulk are predicted to provide a condensed-matter realization of the chiral anomaly. Weyl semimetal has been predicted in different materials.[47,48]
Recent observations of Fermi arcs in the surface state and Weyl nodes in the bulk state of TaAs by ARPES experiments have confirmed it as a non-magnetic Weyl semimetal with non-inversion symmetry for the first time.[49–52] Tantalum mono-arsenide (TaAs) crystallizes in a body-centered tetragonal structure with the space group I41md. The crystal of TaAs can be visualized as an arrangement of regular trigonal prisms of Ta atoms with an arsenic atom at the center. The absence of a horizontal mirror plane in the unit cell makes this structure break the inversion symmetry, which is crucial for realizing a time reversal symmetric Weyl semimetal.[49,50] TaAs has totally 12 pairs of Weyl nodes in one Brillouin zone, which are classified as eight W1 nodes and 16 W2 nodes. It is noteworthy that the nominations of W1 and W2 are opposite in different literatures, and the nomination as that in Ref. [49] is chosen here.
The transport experiments on mono-crystalline TaAs observed large TMR, strong SdH oscillations, and NLMR.[6,53,54] Huang et al. reported that the LMR for B ‖ i ‖ a for TaAs shows a small dip for B < 1 T and then a negative signal up to −30% in 6 T.[54] The LMR changes to positive in higher field, which was explained as a slightly imperfect alignment of the field and the current. Two frequencies of the SdH oscillations for B ‖ c ⊥ i were assigned to the Fermi surfaces enclosing W1 and W2, and the NLMR was ascribed to the chiral anomaly of W1 and W2. Zhang et al. measured LMR in two main crystallographic orientations B ‖ i ‖ a and B ‖ i ‖ c for the samples with different chemical potentials[6] (Fig.
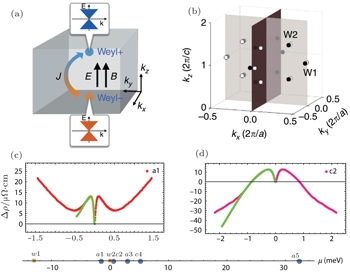 | Fig. 3. Electronic band structure of WSM TaAs and the NLMR (from Ref. [6]). (a) Schematics of the separation of the pairs of Weyl fermions in a WSM in momentum space. (b) The location of the Weyl nodes in the first BZ for TaAs. (c) and (d) The NLMR for two samples with different chemical potentials. The chemical potentials of the samples are illustrated in panel (e). |
The WSM states in the TaAs family were later confirmed in other transition metal monopnictides including NbAs, TaP, and NbP,[57–60] but the observations of the LMR seem to be opposite in different literatures. Wang et al. reported NLMR about −80% at 1.5 K for NbP and ascribed it to the chiral anomaly in the W1 nodes.[61] They found identical LMR below 20 K and described this phenomenon as a quantum behavior due to the protection from the scattering of nonmagnetic impurities. Above 20 K, the intra-valley inelastic scattering between electrons cannot be ignored and the chiral anomaly induced NLMR becomes temperature dependent. However the measurements on NbP in Refs. [62] and [63] did not observe NLMR. Contradictory results of the LMR were also reported for NbAs.[64,65] Negative LMR was reported in single crystals of TaP in Refs. [63] and [66]–[68]. Hu et al. ascribed the NLMR as due to the chiral anomaly.[66] Arnold et al. analyzed the quantum oscillations for TaP and claimed that the Fermi surface forms electron and hole pockets surrounding pairs of Weyl nodes, therefore the chirality is ill-defined in TaP.[68] They claimed that the NLMR can be affected by a magnetic-field induced current jetting effect inside the sample.
A group of transition metal dipnictides MPn2 (M = Nb and Ta, Pn = As and Sb) crystallize in a monoclinic OsGe2-type structure. These isostructrural compounds can be viewed as Zintle phases which contain Pn–Pn dimers and their electron states are balanced as 
The chiral anomaly is also connected with NLMR in a trivial, quasi-2D metal with parabolic band dispersion. Delafossite PdCoO2 crystallizes in a rhombohedral structure in which the mono-atomic triangular layers are stacking along the c axis. This compound is a highly anisotropic 2D-like semimetal with the ratio of anisotropy of the resistance ρc/ρab = 400 (Ref. [75]). Previous ARPES experiment revealed a single, corrugated and nearly 2D Fermi surface with a rounded hexagonal cross-section.[76] Kikugawa et al. reported that the inter-planar LMR along the c axis decreases up to −70% in a magnetic field of 30 T (Fig.
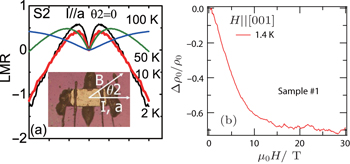 | Fig. 4. The NLMR reported in NbAs2 and PdCoO2. (a) Field dependent LMR for a NbAs2 single crystal at 1.8 K, 10 K, 50 K, and 100 K when B ‖ i ‖ a. Inset: a standard four-point contact geometry. From Ref. [55]. (b) Inter-planar LMR for a PdCoO2 single crystal at 1.4 K. The NLMR persists up to 30 T. From Ref. [56]. |
Some useful transport properties of the samples showing NLMR are collected in Table
| Table 1. Summary of basic electrical transport properties for the recent reported semimetals showing NLMR. . |
Unlike the measurements on bismuth and InSb in the last century, the studies on these topological materials aim to explore the signature of chiral anomaly. However, it is critically important to consider all possible origins for NLMR and to discuss how one can distinguish each of the other origins from the chiral anomaly. For the non-magnetic semimetal, we conclude three possible origins for the NLMR. The first one is the well-known ABJ effect. An NLMR was predicted by Nielsen and Ninomiya beyond the QL,[15] where only zeroth landau level is partially occupied. It was shown that the NLMR due to the chiral anomaly persists to the regime of weak magnetic field.[77–79] In this semi-classical regime, the LMC is proportional to B2, and this is what most literatures reported.
Argyres and Adams predicted that NLMR can occur in non-degenerate semiconductors subjected to a strong magnetic field at low temperatures.[26] Recent theoretical studies indicated that the LMR in the QL can be negative or positive depending on the band dispersion and the nature of the impurities.[80,81] Zhang et al. showed that the LMC can be linearly positive in a small magnetic field in a WSM.[82]
The third explanation is based on the so-called ‘current-jetting’ effect. Early researchers in the last century noticed that the non-uniform current distribution inside the sample can induce an artificial NLMR.[1,25,83,84] The current-jetting-induced NLMR was also observed in some topological trivial metallic elements.[85,86] The NLMR in polycrystalline Ag2Se (Fig.
 | Fig. 5. A voltage drop across the thickness of polycrystalline Ag2Se develops under a longitudinal magnetic field, revealing current jetting effect as the origin of the NLMR. From Ref. [24]. |
Considering the various physical properties of the semimetal showing NLMR in experiment, it is difficult to conclude a single origin of the NLMR. Since some experiments on topological trivial semimetals have shown the NLMR, it is not safe to attribute the NLMR to the chiral anomaly merely depending on the magneto-transport experiment. In order to attribute the NLMR to Weyl fermions, it is crucial to obtain comprehensive information about the band structure of the semimetal and exclude other possible origins such as a current jetting effect. For DSM and WSM, it is important to develop further experiments to reveal the exotic effects associated with the chiral anomaly.[18]
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 | |
| 52 | |
| 53 | |
| 54 | |
| 55 | |
| 56 | |
| 57 | |
| 58 | |
| 59 | |
| 60 | |
| 61 | |
| 62 | |
| 63 | |
| 64 | |
| 65 | |
| 66 | |
| 67 | |
| 68 | |
| 69 | |
| 70 | |
| 71 | |
| 72 | |
| 73 | |
| 74 | |
| 75 | |
| 76 | |
| 77 | |
| 78 | |
| 79 | |
| 80 | |
| 81 | |
| 82 | |
| 83 | |
| 84 | |
| 85 | |
| 86 | |
| 87 |


