Iridium (Ir) is a 5d transition metal of platinum group with a high density of d-states at the Fermi level which is the main hindrance in the theoretical investigation of its lattice properties. It is the second densest metal after osmium and is found in face centred cubic (fcc) structures up to melting temperature. It is different from other fcc transition metals due to some of its unusual physical properties, such as high melting temperature, high electrical conductivity, large shear and bulk moduli and negative Cauchy pressure. It is very hard, brittle and corrosion resistant and its phonon spectra show Kohn anomalies.^[1] Its thermal stability at high temperature and the large shear modulus make it a superior metal for ultra high temperature applications. Physical properties of Ir at high temperature and high pressure are not yet completely known. To understand the behavior of these materials in an extreme environment (high temperature and high pressure), one requires knowledge of thermophysical properties. Such study provides important information about the new materials which are needed in modern technological applications. At high temperature, thermal vibrations (anharmonic effects (AE)) play an important role in the determination of thermophysical properties of materials. At this temperature (near melting temperature), the contribution due to vacancies and thermally excited lattice defects to the physical properties is noticeable. Hence, it is difficult to know the magnitude of contribution due to AE from the above mentioned contributions, which leads to large uncertainties in the study of physical properties of materials at such high temperatures experimentally.^[2] First principle calculations are highly reliable and they are a better supplement of experimental methods for the study of thermophysical properties of materials in an extreme environment, but the study of phonon contribution to thermodynamic properties of materials is beyond the capability of ab-initio approach because it is too complex mathematically and computationally lengthy which is implemented by using certain well defined approximations. In comparison with first principle methods, the other methods based on theoretical modeling are computationally simple and physically transparent and they can explain a wide range of physical properties of different groups of materials not only qualitatively but also quantitatively.

Very recently, many attempts have successfully been made to theoretically investigate the static, lattice dynamical and thermodynamic properties of Ir using first principle methods^[3,4] and other methods^[5,6] including pseudopotential.^[1,2,7–9] All these studies were carried out to theoretically understand the behavior of microscopic properties of materials. However, limited attempts have been made to understand the behavior of materials at extreme condition from macroscopic properties.^[10,11] This fact encouraged us to study the thermophysical properties of Ir at high temperatures.

Recently, Wang and his co-workers^[12–16] proposed a mean-field potential (MFP) approach to account for the vibrational contribution of the lattice ions to the total free energy, which means that the field potential is defined as the potential experienced by a wanderer atom in presence of surrounding atoms which is computed in terms of cold energy. These authors have accounted for the contribution due to thermally excited electrons by computing energy density of states.

In this paper, by using a simple scheme proposed by Bhatt and co-workers,^[17–22] we have studied vibrational contribution to the free energy using mean-field potential approach in conjunction with Krasko–Gurskii (KG)^[23] pseudopotential. The contribution to the free energy due to thermally excited electrons has been accounted for by using Mermin functional.^[24] We have studied volume variation of cold energy (E_c) as well as Helmholtz free energy (F_ion(Ω, T)) at different temperatures along with the equation of state (EOS) at 300 K and shock Hugoniot. Thermal expansion (β_P) isothermal and adiabatic bulk moduli (B_T and B_S), specific heats at constant pressure (C_P) and constant volume (C_V) and enthalpy (E_H) have also been studied in this paper.

The rest of this paper is arranged as follows. In Section 2, we describe the mathematical methods to compute physical properties. In Section 3, our computed results are compared with the available experimental findings and theoretical results. Section 4 is concluding remarks.

The total Helmholtz free energy per atom is given by^[12]

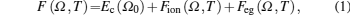
The unscreened KG pseudopotential^[23] has the following form in q space:

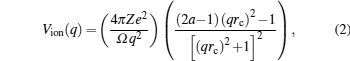
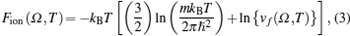
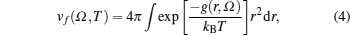
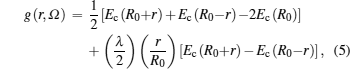
The free energy due to thermal excitation of a free electron gas (F_eg), can be written using Mermin functional^[24] as

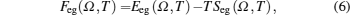
The first step of our calculation is to determine the pseudopotential parameters (a and r_c) appearing in Eq. (2). Following Rosenger et al.,^[28] we kept a = 3.0 and r_c accounting the spatial extension of pseudopotential was determined at zero cold pressure condition. The value of r_c is 0.339 a.u. with valency 4. The calculated values of binding energy, lattice constant, and bulk modulus at 0 K are compared with the experimental and other theoretical results in Table 1.

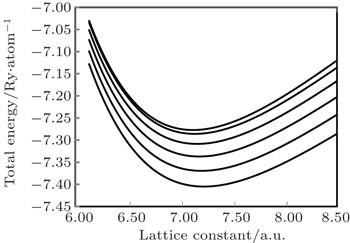
In the present study, the experimental binding energy has been calculated as the sum of experimental values of cohesive energy and ionization energies due to valence electrons,^[29,30] which were taken from Refs. [31] and [32], respectively. Our calculated binding energy is in excellent agreement with the experimental result and the calculated lattice constant has 1.77% variation with the experimental result reported in Ref. [3]. The excellent agreement of the computed binding energy with the experimental result suggests that such energy, known as intermolecular energy which is responsible for holding the individual components of metal together, is properly accounted for. Park et al.^[3] have used van der Waals (vdW) interaction with standard density functional theory (DFT). In their computation, they used five van der Waals density functional (vdW-DF) and five dispersion corrected (DFT-D) vdW functional along with the standard DFT functional of local density approximation (LDA) and generalized gradient approximation (GGA). In the present study, the lattice constant at 0 K has been computed from the minima of static-energy versus the volume curve which is shown in Fig. 1. The best value of lattice constant found by Park et al.^[3] is 7.255 a.u. using DFT D3 vdW functional. In this paper, computed binding energy is in close agreement with their^[3] result of binding energy (7.354 Ry/atom) for the DFT D3 vdW functional. Our computed value of lattice constant is very close to the result obtained by using standard DFT functional of LDA which is also shown in Table 1 and corresponding binding energy for this functional is 8.375 Ry/atom which is in 17.40% variation with the experimental result. Our result is better than the theoretical result obtained by Katsnelson et al.^[1] who have carried out study using Animalu–Heine pseudopotential (AH) and modified Animalu–Heine pseudopotential (MAH) form factors. It is important to note that Katsnelson et al.^[1] have used effective valency (4.5) instead of its actual valency (4). Greenberg et al.^[9] used Animalu–Heine pseudopotential with different values of valency (Z), such as Z = 4.0, Z = 4.5, Z = 3.5, and Z = 4.5 with Born–Mayer interaction term, Z = 4.5 with second-order correction to energy and Z = 4.5 with third order correction to energy to study physical properties of Ir including binding energy and bulk modulus at 0 K. Results obtained with these different values of Z are differentiated in Table 1 by superscripts. The computed value of binding energy is also better than the result obtained by Greenberg et al. The computed value of bulk modulus at 0 K is in 30.64% variation with the experimental result^[3] which is inferior to other theoretical results.

Table 1.

Table 1.

Table 1. The comparison of computed lattice constant (R0 in a.u.), binding energy (−E in Ry/atom), and static bulk modulus (B0 in GPa) with experimental and other theoretical results. . Present Expt. Others R0 7.133 7.259[3] 7.255 (DFT D3),[3] 7.220 (LDA)[3] −E 7.277 7.276 9.064 (AH),[1] 9.060 (MAH),[1] 7.210a,[9] 8.947b,[9] 5.591c,[9] 9.415d,[9] 9.036e,[9] 9.02f[9] B0 283.507 355.0[3] 342.0,[7] 312.7 (AH),[1] 292.6 (MAH),[1] 354.3a,[9] 325.8b,[9] 359.2c,[9] 387.7d,[9] 339.9e,[9] 348.4f[9] Animalu–Heine pseudopotential with different values of valency: a Z = 4.0, b Z = 4.5, c Z =3.5, and d Z = 4.5 with Born–Mayer interaction term. e Z = 4.5 with second-order correction to energy. f Z =4.5 with third-order correction to energy.

Table 1. The comparison of computed lattice constant (R0 in a.u.), binding energy (−E in Ry/atom), and static bulk modulus (B0 in GPa) with experimental and other theoretical results. .

The Helmholtz free energy as a function of temperature is computed by using Eq. (1). The volume variation of Helmholtz free energy at temperatures 500 K, 1000 K, 1500 K, 2000 K, and 2500 K along with the cold energy is shown in Fig. 1. The minima of such curves give the theoretical values of lattice constants at corresponding temperatures.

Fig. 1.

	Figure Option ViewDownloadNew Window
	Fig. 1. The volume variations of cold energy and Helmholtz free energy. From top to bottom graphs, the curves correspond to temperatures: T = 0 K, 500 K, 1000 K, 1500 K, 2000 K, and 2500 K, respectively.

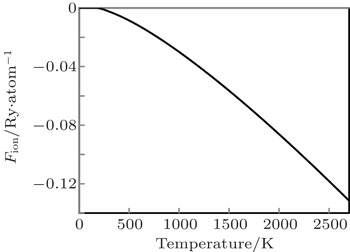
The variation of free energy due to lattice ion (F_ion) against temperature is shown in Fig. 2. In the absence of experimental results as well as theoretical results at higher temperatures, we could not compare our result. But our observed trend of F_ion is in accordance with the theoretical result obtained by Ahmed et al.^[33] who have carried out first principle calculation up to 500 K by using pseudopotential plane wave (PP-PW) method. Bhatt et al.^[17,18] have used MFP approach in conjunction with pseudopotential to study temperature variation of F_ion. The behavior of F_ion with temperature obtained presently is also similar to the behavior observed by Bhatt et al. From Fig. 2, it is clearly seen that the F_ion increases more rapidly and faster with the increase in temperature. The reason for the increase in F_ion is the increase in the amplitude of vibration of ions due to the large volume with the increase in temperature.

Fig. 2.

	Figure Option ViewDownloadNew Window
	Fig. 2. The variation of free energy due to lattice ion (Fion) against temperature.

The behavior of the expansion of material with temperature can be understood by studying coefficient of volume-thermal expansion (β_P) which is defined as^[12]

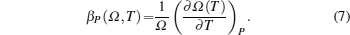
During the literature survey, we observed that different authors have reported the values of linear, volume and relative volume thermal expansions (Ω/Ω₀, where Ω and Ω₀ are volumes at given temperature and 0 K, respectively). In order to compare our computed results of volume thermal expansion with the experimental and other theoretical results, we have converted the results in the form of relative volume thermal expansion. The temperature variation of relative volume thermal expansion along with the experimental findings^[34–37] and other theoretical results^[5,38] is shown in Fig. 3.

Fig. 3.

	Figure Option ViewDownloadNew Window
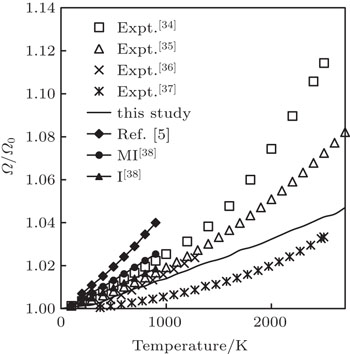	Fig. 3. Relative volume thermal expansion as a function of temperature. Here, “I” represents pseudopotential of Ivanov, while “MI” represents the modified form of the pseudopotential of Ivanov.

To the best of our knowledge, for the first time, in this paper, we have carried out the study of thermal expansion of Ir up to melting temperature because, at higher temperatures, the experimental results of β_P change appreciably and the theoretical studies are limited up to 900 K. By conducting a detailed comparison of our results with experimental results, we find that our results are almost identical to experimental results obtained by Touloukian et al. (recommended values) up to 1500 K.^[34] The maximum deviation of our computed results with the results obtained by Touloukian et al. is 6.9% at 2500 K. The results obtained by Arblaster^[35] are also in good agreement with 2.78% variation at 2500 K. The results obtained by Caldwell^[36] are in excellent agreement with our computed results up to 1300 K. The results obtained by Halvorson^[37] are in excellent agreement with our theoretical results at low temperature and high temperature with maximum deviation of 1.05% at 1800 K. Our computed results are also better than the theoretical results obtained by Ferah et al.^[5] and Katsnelson et al.^[38] Ferah et al.^[5] used molecular dynamics simulations by using modified Morse potential and employed embedded atom method (EAM) to study temperature variation of thermal expansion. Katsnelson et al.^[38] used pseudopotential obtained by Ivanov et al. (I) and modified form of the pseudopotential of Ivanov et al. (MI) to study the temperature variation of thermal expansion. From such detailed comparisons, we find that the simple method used in this paper properly accounts for anharmonic effects.

The EOS which is a fundamental property of material plays a crucial role in understanding a wide range of physical properties of material in condensed matter physics. For modeling the Earth’s core and planetary interiors, it is one of the important parameters. EOS is very useful in geophysics, astrophysics, and material science. Static EOS at ambient temperature which is largely governed by cold energy provides a link to monitor microscopic internal structure of the material. 300 K EOS has been computed by using the following equation:

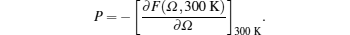
Our computed P–Ω isotherm at 300 K is compared with experimental findings^[39] as well as theoretical results^[38,39] in Fig. 4 up to 40% compression. Nemoshkalenko et al.^[39] have obtained experimental as well as theoretical results which are in excellent agreement with the present results. In theoretical study, Nemoshkalenko et al. have used Animalu–Heine–Abarenkov local pseudopotential along with exchange and correlation function of Taylor to study EOS. They have adjusted four parameters (two pseudopotential parameters and two Born–Mayer parameters) through a least square fit of the experimental value of phonon frequency and the elastic moduli at equilibrium volume. Katsnelson et al.^[38] studied EOS at 295 K theoretically by using pseudopotential obtained by Ivanov et al. (I) and performed first principle calculation by modification in pseudopotential obtained by Ivanov et al. (MI).

Fig. 4.

	Figure Option ViewDownloadNew Window
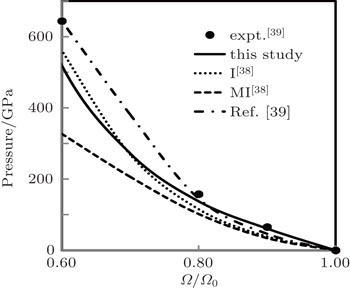	Fig. 4. Our computed P–Ω isotherm at 300 K compared with experimental findings[39] as well as theoretical results[38,39] up to 40% compression.

Our results are in excellent agreement with the results obtained by Katsnelson et al.^[38] using I for all compression range and in excellent agreement for smaller compressions up to 20% and in reasonably good agreement at higher compressions using MI. From above comparison, we find that our results are better than other theoretical results,^[38,39] which confirm the applicability of local form of the pseudopotential used in the present calculation which has only one adjustable parameter r_c (core radius). Further, EOS is a test of approximations used in the theory for the electron–electron interaction which seems to be properly accounted for.

The internal energy or enthalpy at zero pressure is given by^[12]

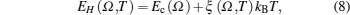
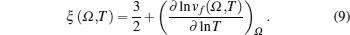
Temperature dependence of computed values of relative or scaled enthalpy (E_H(T)−E_H(300 K)) up to melting temperature and the experimental results up to 1800 K obtained by Robie et al.^[40] and the theoretical results up to 900 K obtained by Ferah et al.^[5] are compared in Fig. 5. Our results are almost identical with the experimental results in Ref. [40] up to 1500 K with maximum deviation of 18.71% at 1800 K, and our results are also in excellent agreement with the theoretical results obtained by Ferah et al.^[5]

Fig. 5.

	Figure Option ViewDownloadNew Window
	Fig. 5. Relative enthalpy as a function of temperature.

The isothermal (B_T) and adiabatic (B_S) bulk moduli are calculated using the following equations:^[10]

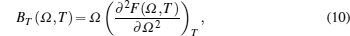
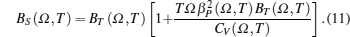
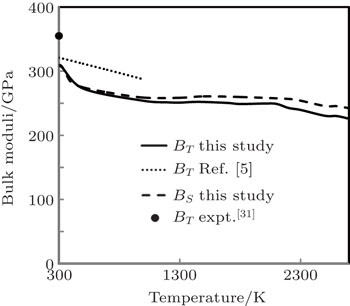
The temperature variation of our computed results of isothermal and adiabatic bulk moduli up to melting temperature and the theoretical results of B_T obtained by Ferah et al.^[5] (up to 1000 K) along with the experimental point of B_T at 300 K^[31] are displayed in Fig. 6.

Fig. 6.

	Figure Option ViewDownloadNew Window
	Fig. 6. Bulk moduli as a function of temperature.

At 300 K, the computed result of B_T has 14.92% variation with the experimental value,^[31] which is better than the result of B_T at 0 K^[3] with 30.64%variation. Such observation reveals that percentage variation of B_T with the experimental result decreases with the increase in temperature. In the absence of experimental results, at higher temperature, one can say that our approach explains anharmonocity at higher temperatures in a better way. Our computed results of B_T are in good agreement (having 3.71% variation at 300 K and 11.60% variation at 1000 K) with the theoretical results obtained by Ferah et al.^[5] In the absence of experimental and theoretical results of B_S, we could not compare it.

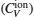
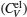
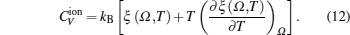
The total contribution of specific heat at constant volume (C_V) arises due to contributions from atomic vibrations and thermally excited electrons . It plays an important role in the understanding of phase transition of materials. Specific heat due to lattice ions at constant volume is given by^[12]

The total constant volume heat capacity (C_V) and the constant pressure heat capacity (C_P) are given by the following equations:^[10]

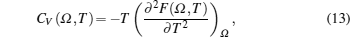
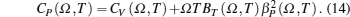
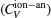
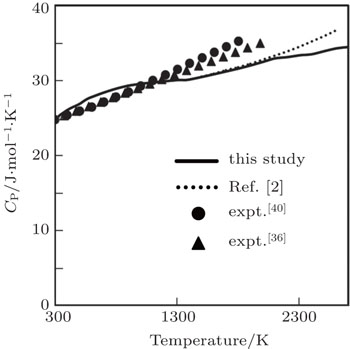
Anharmonic contribution to the heat capacity can be obtained by subtraction 3k_B from . Computed results of C_P as a function of temperature are compared with the experimental findings^[36,40] as well as the theoretical results^[2] (from 1500 K to 2600 K) as shown in Fig. 7.

Our computed results of C_P are in excellent agreement with the experimental results (up to 1800 K) obtained by Robie et al.^[40] The variation increases with the increase in temperature with maximum variation of 11.60% at 1800 K. The experimental results of C_P obtained by Caldwell^[36] are also in excellent agreement with the present result with 7.60% variation at 2000 K. Our computed results of C_P are also in excellent agreement with the theoretical results obtained by Katsnelson et al.^[2] who have used pseudopotential of Animalu and Heine in the framework of second-order perturbation theory.

Fig. 7.

	Figure Option ViewDownloadNew Window
	Fig. 7. Specific heat at constant pressure as a function of temperature.

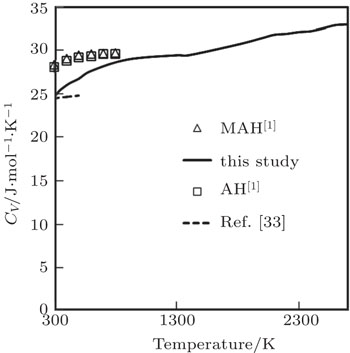
The temperature dependence of our computed results of C_V along with the corresponding other theoretical results^[1,33] is displayed in Fig. 8.

Fig. 8.

	Figure Option ViewDownloadNew Window
	Fig. 8. Specific heat at constant volume as a function of temperature.

Our computed results of C_V are in excellent agreement with the theoretical results obtained by Katsnelson et al.^[1] and Ahmed et al.^[33] Ahmed et al.^[33] used a special ab-initio density functional theory along with pseudopotential plane wave (PP-PW) method, by using Vanderbilt formalism with local density approximation (LDA) for the exchange and correlation energy of electrons. Katsnelson et al.^[1] studied C_V by using Animalu–Heine pseudopotential (AH) and also with modification in Animalu pseudopotential (MAH). Authors^[1] have used effective valency 4.5 instead of actual valency. Here, we would like to point out that during calculation, the volume variation with temperature in the calculation of C_V was not considered in Ref. [1].

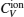
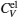
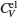
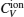
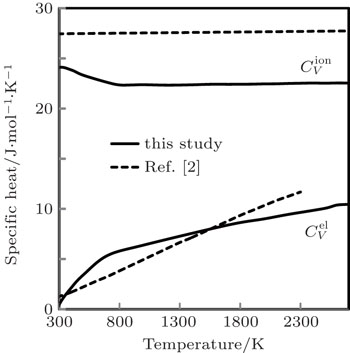The computed results of and along with the corresponding theoretical results^[2] as a function of temperature are shown in Fig. 9. Our computed temperature variation of is in excellent agreement and is in good agreement with the theoretical results.^[2]

Fig. 9.

	Figure Option ViewDownloadNew Window
	Fig. 9. Specific heats due to lattice ions and thermally excited electrons as a function of temperature.

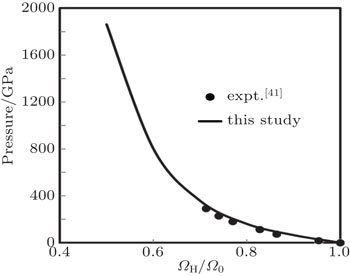
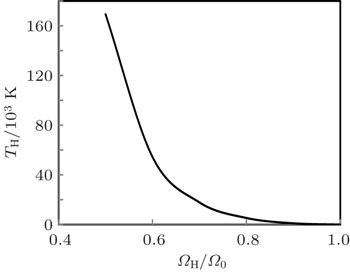
In the shock-wave experiment, a supersonic wave is passed through the material which produces simultaneous high temperature and high pressure. The dynamic EOS or shock-Hugoniot or simply Hugoniot is defined as the locus of all possible states that can be reached by using a single shock from a given initial state, usually defined by thermodynamic variables like pressure, volume and internal energy or enthalpy. The Rankin–Hugoniot equation is given by

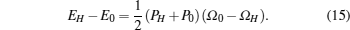
Here, P_H, Ω_H, and E_H are pressure, volume, and energy of the compressed state while P₀, Ω₀ and E₀ are corresponding quantity under ambient condition. Equation (15) defines a compression curve (Ω_H versus P_H) known as Hugoniot as a function of known Hugoniot energy (E_H). Temperature along the Hugoniot (T_H) can be in the range of room temperature to several tens of thousands degrees of kelvin. Thus, shock Hugoniot explains the behavior of material under simultaneous high temperature and high pressure. Results of Hugoniot pressure as a function of fraction of volume are displayed in Fig. 10 along with experimental results^[41] which are in excellent agreement. Such success reveals that the present scheme can be used to account for the anharmonicity in the theoretical calculation of thermodynamic properties.

Fig. 10.

	Figure Option ViewDownloadNew Window
	Fig. 10. Results of Hugoniot pressure as a function of fraction of volume.

Volume variation of temperature along Hugoniot (T_H) is shown in Fig. 11. We could not compare our results in the absence of experimental or other theoretical results of T_H.

Fig. 11.

	Figure Option ViewDownloadNew Window
	Fig. 11. Calculated Hugoniot temperature as a function of the reduced volume.

We have carried out a theoretical study of the thermophysical properties of Ir using a simple local form of the pseudopotential in conjunction with MFP approach at high temperature (up to melting temperature) and high pressure. The computed results of thermophysical properties at different temperatures are in excellent agreement with the experimental findings as well as the results obtained by using first principle methods. Such success reveals that the anharmonic effect which plays a vital role in the determination of thermophysical properties of materials at higher temperatures is included properly in the present conjunction scheme. One of the most important advantages of the MFP approach used in the study is that it accurately bypasses the lengthy and intricate calculations required for the calculation of F_ion using the phonon density of states. In such an approach, for the theoretical calculation of the lattice constant as a function of temperature, one requires volume variation of phonon density of states at each temperature. Our results also confirm that the accurate description of the thermophysical properties at higher temperature can be done by including the effect of electron–electron interaction which can be explained by using Mermin functional instead of calculating energy density of states.^[12] In our opinion, the pseudopotential approach is computationally simple and physically transparent, at the same time; it generates accurate results in an extreme environment which are comparable with first principle methods. The local form of pseudopotential (KG) with only one adjustable parameter r_c (determined from zero pressure condition at 0 K) is found to be transferable without changing its value at extreme environment during calculation. Further, the present calculation is free from any kind of adjustment of valency and does not require a Born–Mayer-type potential to account core–core repulsion.^[1,2,9] Moreover, as used by many researchers,^[1] in the present scheme, we do not require an extra analytical form of the potential in q space which is added to pseudopotential for the better description of many thermodynamic properties. In that sense, s–p–d hybridization is accounted for properly in the pseudopotential itself.