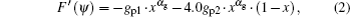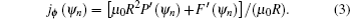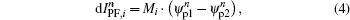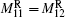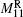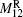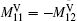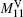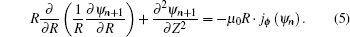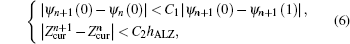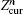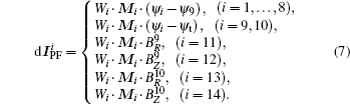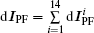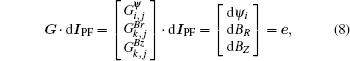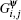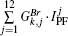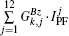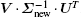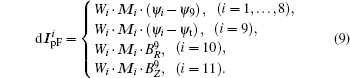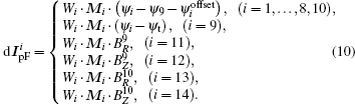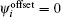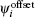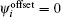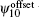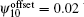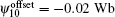Cite this Article
Guo Yong, Xiao Bing-Jia, Liu Lei, Yang Fei, Wang Yuehang, Qiu Qinglai. A divertor plasma configuration design method for tokamaks. Chinese Physics B, 2016, 25(11): 115201  
Permissions
A divertor plasma configuration design method for tokamaks
Guo Yong1, Xiao Bing-Jia1, 2, Liu Lei1, †, , Yang Fei3, Wang Yuehang4, Qiu Qinglai1
Institute of Plasma Physics, Chinese Academy of Science, Hefei 230031, China
School of Nuclear Science and Technology, University of Science and Technology of China, Hefei 230026, China
Department of Computer Science, Anhui Medical University, Hefei 230026, China
CAS Key Laboratory of Basic Plasma Physics and Department of Modern Physics, University of Science and Technology of China, Hefei 230026, China

 

† Corresponding author. E-mail: liulei@ipp.ac.cn

Project supported by the National Magnetic Confinement Fusion Research Program of China (Grant Nos. 2014GB103000 and 2014GB110003), the National Natural Science Foundation of China (Grant Nos. 11305216, 11305209, and 11375191), and External Cooperation Program of BIC, Chinese Academy of Sciences (Grant No. GJHZ201303).

Abstract
Abstract

The efficient and safe operation of large fusion devices strongly relies on the plasma configuration inside the vacuum chamber. It is important to construct the proper plasma equilibrium with a desired plasma configuration. In order to construct the target configuration, a shape constraint module has been developed in the tokamak simulation code (TSC), which controls the poloidal flux and the magnetic field at several defined control points. It is used to construct the double null, lower single null, and quasi-snowflake configurations for the required target shape and calculate the required PF coils current. The flexibility and practicability of this method have been verified by the simulated results.

PACS: 52.55.Fa;52.65.–y;52.50.Nr
Keyword:plasma divertor configuration;tokamak simulation code;EAST;plasma shape design
1. Introduction

The efficient and safe operation of large fusion devices relies on the proper plasma configuration inside the vacuum chamber. For the plasma configuration design, we should consider the following aspects: (i) maintaining adequate clearance from the chamber wall to avoid high density of power and particle deposition, (ii) close to the passive plate to ensure adequate passive stabilization, (iii) coupling with the antenna for efficient radio frequency (RF) heating, (iv) reducing the MHD activity, (v) optimizing the magnetic field around the strike point to reduce heat deposition, and so on.[1] So, it is important to develop a method to design the plasma configuration, especially for the detail feature of the divertor configuration.

The tokamak simulation code (TSC)[2,3] is a numerical model of the axisymmetric tokamak plasma and the associated control systems. It evolves the magnetic field in a rectangular computational domain using the Maxwell MHD equations for the plasma, coupled through the boundary conditions to the circuit equations for the poloidal field (PF) coils. The TSC code could be used for the static equilibrium calculation while the evolution calculation is switched off. In the original code, the plasma position could only be controlled by the plasma radial and vertical position through the ‘observation pair’ control method. The other configuration parameters, such as the elongation, triangularity, strike point, and so on, are decided by the preprogrammed currents, which are adjusted manually. It is time-consuming and less efficient. Sometimes, it is difficult to get the desired configuration exactly.

In order to solve this problem, a shape constraint module has been developed in the TSC code to construct the configuration. The work is briefly introduced in Section 1. Section 2 gives the original TSC model for the static equilibrium calculation. In the TSC code, the shape constraint module has been developed and used for the Experimental Advanced Superconducting Tokamak (EAST) divertor configuration design. The results of double null, lower singular null, and quasi-snowflake configuration are given in Section 3. Finally, the conclusion is given in Section 4.

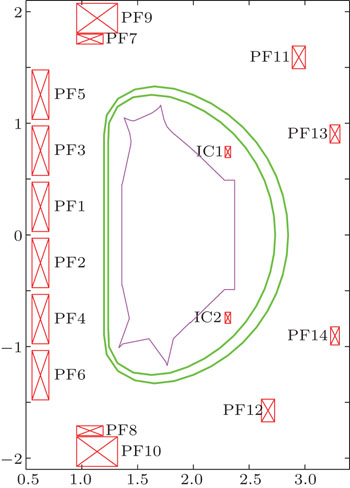
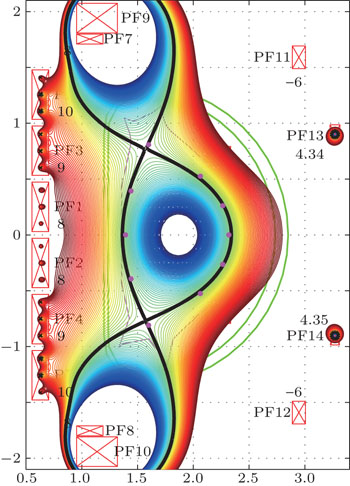
2. TSC original model for EAST configuration design

EAST[4] is a full superconducting tokamak with D-shaped cross-section, as shown in Fig. 1, which allows the plasma to be flexibly shaped with elongation of 1.5–2, triangularity of 0.3–0.6, major radius of 1.8 m, and minor radius of 0.4 m. There are 14 poloidal field (PF) coils to shape the plasma and 2 inside coils (IC1 and IC2) for the fast vertical position control, which are signed by the red box. The coordinates of these coils in EAST are listed in Table 1. The designed maximum allowed current in the PF coils is 14 kA/turn. Because PF7 and PF9, PF8 and PF10 are connected together respectively in EAST, 14 PF coils are divided into 12 coil groups in TSC. The vacuum vessel has a double-layer SS-316LN structure with 8 mm thickness of each layer, which is shown as the green lines. These two layers of the vacuum vessel are modeled as 316 filaments in TSC. Each filament is defined as a toroidally continuity conductor with about 300 μΩ. The passive plates are cut into 8 toroidally disconnected pieces in EAST, and each of them is connected to the vacuum vessel through supporting legs. In TSC, the passive plates are modeled as toroidally continuous filaments which have a verified equivalent resistivity of 1.09 μΩ·m.[5] Finally, the active and passive conductor model of EAST is built in TSC.

Fig. 1. EAST geometry poloidal field (PF) locations and sizes are signed by red rectangle boxes, the double layer vacuum vessels are signed by green lines.
Table 1.

PF coils geometry and turns in R and Z directions.

.

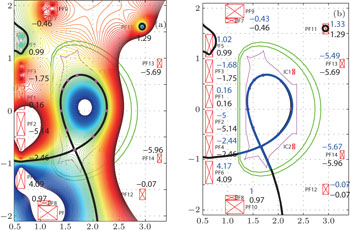
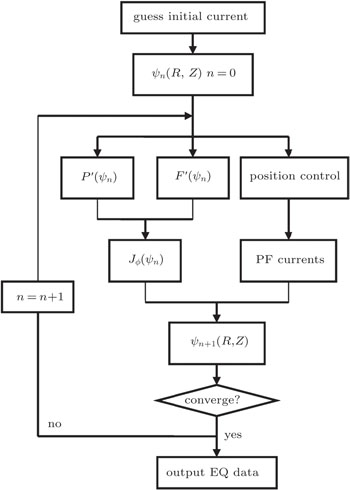
The diagram of TSC static equilibrium calculation is shown in Fig. 2. At first, the initial currents of the plasma and the active coils are guessed. For the plasma current, besides the total plasma current, the plasma current center also should be preset, and the initial plasma current is assumed as a filament at the plasma current center for the plasma startup phase. For the active coils, according to the experiment data or experience, the feed-forward PF currents are preprogrammed. The IC coils are responsible for the fast control of the plasma vertical position, the preprogrammed current is always set to zero in the calculation. With such current sources, the initial poloidal flux distribution ψ0 (R,Z) is calculated. In TSC, the plasma pressure P(ψ) and toroidal field function F′(ψ) are assumed to have the following analytical forms:

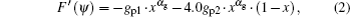
where x is the normalized poloidal flux varying from 0 at the magnetic axis to 1 at the plasma boundary. gp1 and gp2 are calculated to fit the prescribed plasma current and central safety factor q(0) in each iteration. We could adjust the values of P0, αP, and αg to obtain the desired poloidal beta βP and internal inductance ℓi. The new plasma current distribution jϕ (ψn) is calculated by

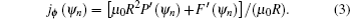
Fig. 2. Iteration loop for the plasma equilibrium construction.

The plasma position is controlled by the observation pair method, which makes the two points of the observation pair at the same poloidal flux surface by correcting the PF current as follows:

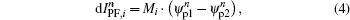
where Mi is the weight for the i-th PF current. According to the desired configuration, the inner and the outer points at the mid-plane are chosen as one observation pair for the plasma radial position control, while two points at the plasma boundary with the same radial position are used for the vertical position control. Correspondingly, the PF coils are regrouped for the plasma radial and vertical position control. PF13 and PF14 coils are set as one group for the plasma radial position control, while . 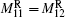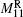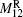and are the weights of PF13 and PF14 to correct the plasma radial position, respectively. These two coils are also set as another group for the plasma vertical position feedback, while . 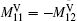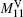and are the weights of PF13 and PF14 to correct the plasma vertical position, respectively. The updated PF coils current is equal to the last iteration current plus the feedback current.

With the updated plasma current and PF currents, the poloidal flux distribution is renewed by solving the equation

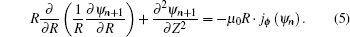
The iteration will continue until the following convergence criteria (shown in Fig. 6) are met:

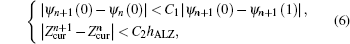
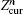
where ψn (0) and ψn (1) are the poloidal fluxes at the magnetic axis and the boundary at the n-th iteration, respectively. is the vertical position of the plasma current center at the n-th iteration, while hALZ is one half the height of the defined TSC computational region. C1 and C2 are the coefficients of the convergence criteria on the poloidal flux and the vertical position for equilibrium, respectively. Obviously, the original TSC model only considers the plasma radial and vertical position control by PF13 and PF14 coils. In the configuration design, the feed-forward PF current should be tested manually to find the proper value for the expected plasma shape. It is time-consuming and less efficient.

3. Shape constraint module and results

In order to improve the efficiency and accuracy of the configuration design, a shape constraint module has been built in the TSC code. Besides the basic radial and vertical position control, the plasma configuration is shaped by constraining the poloidal flux and magnetic field at several special positions. In this section, the shape constraint module is introduced for the double null (DN), lower single null (LSN), and quasi-snowflake (QSF) configurations and several design results are given.

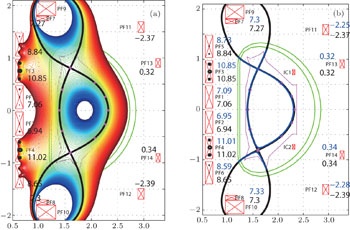
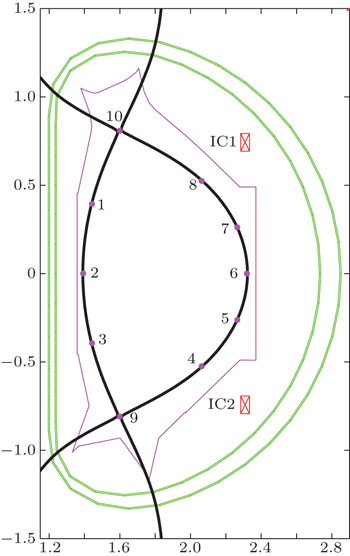
3.1. Double null configuration

The double null configuration has two active X-points (upper and lower X-points) with the same poloidal flux, i.e., plasma boundary flux ψbdry. As shown in Fig. 3, 10 points, including 2 active X-points, are chosen to describe the plasma shape. Points 2 and 6 are grouped as one observation pair for the radial position control, while points 4 and 8 are grouped as the other observation pair for the vertical position control. At the same time, points 1–8 are kept at the plasma boundary by controlling ψi − ψ9 to zero. For the two X-points, they are null points firstly, which means that the radial and vertical magnetic fields (BR and BZ) should be zero. Meanwhile, we could shift the flux linkage at the plasma boundary to ψt by controlling ψ9 − ψt and ψ10 − ψt to zero. Totally, there are 14 parameters that should be controlled to get the expected double null configuration in this case. Finally, after considering all the above constraint conditions, we obtain the corrected PF current for the i-th control parameters

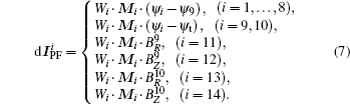
Fig. 3. The control points for the DN plasma configuration design.

The total corrected PF current for the shape constrain is 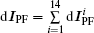. The Wi and Mi are the weight and the PF current distribution for the i-th control parameters, respectively.

As we know, the poloidal flux and the magnetic field change due to the PF current can be represented as

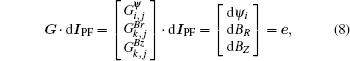
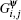
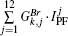
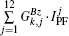
where is the mutual inductance between the j-th PF current (j = 1, …, 12) and the i-th control point (i = 1,…,10), while the radial and vertical magnetic fields at the k-th (k = 1, 2) point are and , respectively. Let G = U · Σ · VT be its singular value decomposition in economy form, i.e., U is a 14 × 12 matrix, V is a 12 × 12 unitary matrix, and Σ is a 12 × 12 diagonal matrix, i.e., Σ = diag (σ1,…,σ12). UTU = I12, and VTV = I12.[6] The smaller σ means the more detailed feature of the plasma shape and the higher requirements on the PF currents. Sometimes, a truncation is required for the balance of the accuracy of the shape and the PF current cost, and form Σnew. M matrix, M = [M1,…,Mi,…,M14], is calculated by .

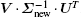
Table 2 lists one group of pre-programmed PF currents used for the DN plasma configuration design. Figure 4 gives the plasma configuration constructed by the original method, in which the radial and vertical positions are controlled by correcting the PF13 and PF14 currents. It is obvious that the two points of one observation pair (points 2 & 6 and points 4 & 8) are constrained to one poloidal flux surface, but not the plasma boundary as desired. So, the PF1–PF12 should be tuned to shape the plasma. For this equilibrium, the flux linkage at the plasma boundary is −0.6994 Wb/rad, which is basically decided by the pre-programmed PF current.

Table 2.

With preprogrammed PF current, TSC constructs the DN configuration with corrected PF current.

.
Fig. 4. With the preprogrammed PF current listed in Table 2, the plasma position is controlled by the observation pair method. The magenta points show the outline of the desired shape.

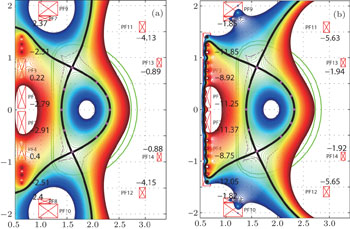
By using the new shape constraint method, for case 1 in Table 2, the flux linkage at the plasma boundary ψt is defined as −0.6994 Wb/rad. All 12 independent PF currents are corrected to obtained the desired plasma configuration, as shown in Fig. 5(a). The first 8 points are close to the plasma boundary with less than 1.0 × 10−3 Wb/rad error. The X-points of the constructed equilibrium are at (1.599, −0.807) and (1.599, 0.807), very close to the X target positions (1.600, −0.808) and (1.600, 0.808). The flux linkage of this constructed equilibrium is −0.6962 Wb/rad, with 0.0032 Wb/rad error. For this case, the measurements of EAST’s 35 flux loops and 38 magnetic probes are calculated by the TSC code. With these measurements and PF currents, the equilibrium is constructed by the EFIT code, as shown in Fig. 5(b), which is superimposed on the TSC designed shape.

Fig. 5. (a) The TSC constructed plasma equilibrium with boundary flux ∼ −0.6962 Wb/rad (case 1 in Table 2), (b) the EFIT reconstructed shape (blue), which is compared with the TSC results (black).

In order to check the flexibility of the flux-linkage shift, case 2 with −0.0036 Wb/rad (target: 0.0 Wb/rad) and case 3 with 0.5912 Wb/rad (target 0.60 Wb/rad) are shown in Fig. 6 and the required PF current is listed in Table 2.

Fig. 6. The constructed plasma equilibrium with flux-linkage at the plasma boundary equal to −0.0036 Wb/rad ((a) case 2 in Table 2) and 0.5912 Wb/rad ((b) case 3 in Table 2).
3.2. Lower single null configuration

The lower single null configuration has one active X-point at the lower plane with the plasma boundary flux ψbdry. Take the case in Fig. 7 as an example, 9 control points are selected, and the corrected PF currents are defined as follows:

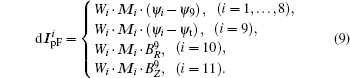
Fig. 7. The control points for the LSN plasma configuration design.

The calculation of Mi is similar to that in the DN case. The preprogrammed PF currents are set to the same values of the DN case (see Table 3). Figure 8(a) gives the constructed plasma LSN configuration with flux-linkage of 0.0046 Wb/rad (target: 0.0 Wb/rad) at the plasma boundary. The error of the control point to the plasma boundary is less than 1.0×10−3 Wb/rad. The X-point locates at (1.654, −0.739) for the constructed equilibrium, close to the X target position (1.650, −0.750). With the magnetic measurements and PF currents provided by TSC, we use the EFIT code to reconstruct this equilibrium. The result is given in Fig. 8(b), which matches the TSC designed configuration well.

Table 3.

With preprogrammed PF current, TSC constructs the LSN configuration with corrected PF current.

.
Fig. 8. (a) The TSC constructed plasma equilibrium with boundary flux ∼ 0.0046 Wb/rad (case 1 in Table 3), (b) the EFIT reconstructed shape (blue), which is compared with the TSC results (black).

Furthermore, the same plasma shapes with −0.5946 Wb/rad (target: −0.6 Wb/rad) and 0.6038 Wb/rad (target: 0.6 Wb/rad) are easily constructed by this method, as shown in Fig. 9.

Fig. 9. The constructed plasma equilibrium with flux-linkage at plasma boundary equal to −0.5946 Wb/rad ((a) case 2 in Table 3) and 0.6038 Wb/rad ((b) case 3 in Table 3).
3.3. Quasi-snowflake configuration

Reducing heat load on the divertor plates is one of the most challenging works for a tokamak reactor. Some advanced configurations with a stronger flaring of poloidal field in the divertor, such as snowflake divertor configuration (SFD), have been proposed.[7,8] SFD requires not only the first-order null point as the usual divertor configuration (i.e., Bp = 0), but also the second-order derivative of the poloidal flux to be zero (i.e., ∇2ψp = 0). Due to the limitation of the PF coils ability, EAST could only operate with the quasi-snowflake (QSF) configuration with Ip ≤ 250 kA.[9–11]

Fig. 10. QSF configuration target with 10 selected control points to sign the outline of the shape.

Different from the standard SFD configuration, QSF has a second X point (X2 point) close to the active X point. Through changing the position of the X2 point, we could obtain different flux expansion and strike point. In EAST, the PF system is not designed for the snowflake configuration. There are only 3 coils (PF6, PF8/10, and PF12) to shape the poloidal flux distribution near the divertor region. Comparing with the LSN configuration, the QSF configuration is constructed by increasing PF6 and PF12 currents, and decreasing PF8/10 current. Obviously, PF6 has a strong effect on the plasma low triangularity, PF8/10 decides the plasma elongation, and PF12 takes part in the control of plasma radial and vertical position with PF11, PF13, and PF14. To maintain the bulk plasma body, the other PF currents are modified to offset the impact. In the original method, we could only control the radial and vertical position, and tune the 12 PF preprogrammed currents by hand close to the desired configuration.[11] It is very inconvenient for the QSF configuration design.

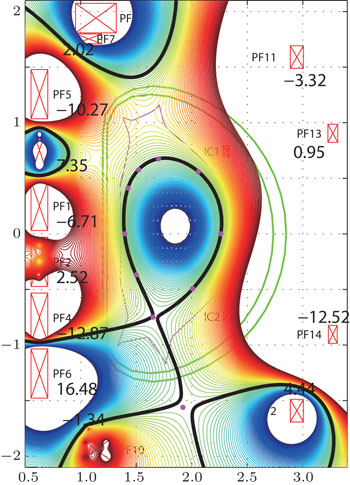
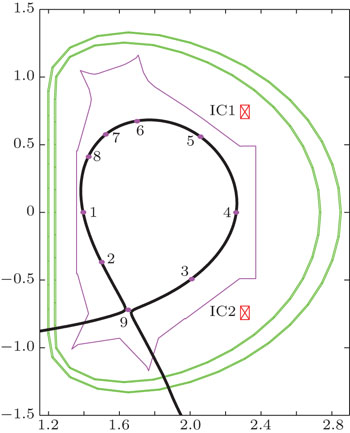
Fig. 11. The flux-linkage at the plasma boundary is set to zero. The constructed QSF configuration with all offset fluxes being zero (case 1 in Table 4).

Figure 10 shows one QSF configuration for EAST with the 10 control points signed by magenta points. In the shape constraint module, the corrected PF current for the i-th control parameters is given as

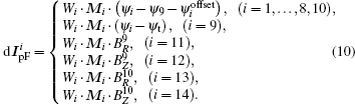
Normally, points 1–8 should be confined at the plasma boundary as 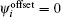. We could make a small shift of the plasma shape by adding offset flux 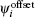to reduce the PF current requirement. The desired flux-linkage at the plasma boundary could be defined as ψt. As X and X2 points, points 9 and 10 should be null points with Br = 0 & Bz = 0. The preparation of the M matrix is similar to that in the DN case.

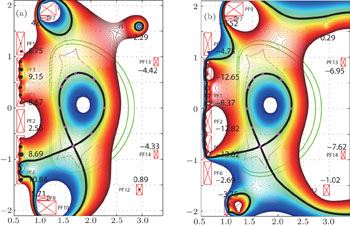
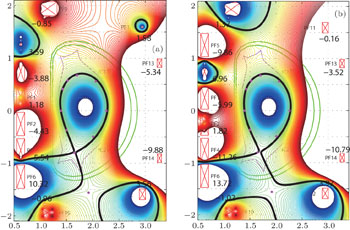
As the former, the preprogrammed PF currents are set the same as those in the DN case (see Table 4). All offsets are set to zero, i.e., 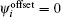(i = 1, …, 8, 10). The target flux-linkage at the plasma boundary is set to zero, i.e., ψt = 0. The designed configuration is shown in Fig. 11. The errors of all control points to the plasma boundary are less than 0.001 Wb/rad. The constructed X point is at (1.671, −0.743), whose target value is (1.65, −0.75). There are 6 parameters that should be controlled for X and X2 points, which is more than that for the DN & LSN configurations, so the accuracy is less than that in those two cases. Basically, the designed configuration is close to the target shape. Focus on the required PF currents listed in Table 4. PF 6 needs 16.48 kA/turn, which is larger than 14 kA/turn (PF current limitation), and the currents of PF4, PF5, and PF14 are very close to the limitation. Obviously, it is not suitable. To fix this problem, offset is used to reshape the target shape. Figure 12(a) shows the new QSF configuration with −0.03 Wb offset added to the 3rd, 4th, and 5th points. All required PF currents are reduced to the limitation of the PF coils ability. Then, EFIT is used to reconstruct the equilibrium to check the designed configuration by TSC. The plasma shape reconstructed by EFIT is shown in Fig. 12(b), which is compared with the TSC designed configuration.

Table 4.

With preprogrammed PF current, TSC constructs the QSF configuration with corrected PF current.

.
Fig. 12. (a) The TSC constructed QSF equilibrium with −0.03 Wb offset fluxes at 3rd, 4th, and 5th points (case 2 in Table 4), (b) the EFIT reconstructed shape (blue), which is compared with the TSC results (black).

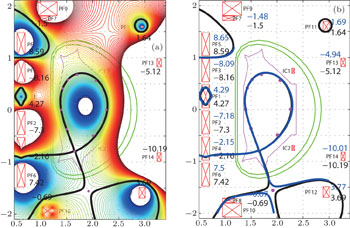
Of course, we could add a strike point as a control point, like points 1–8, and make its poloidal flux the same as the plasma boundary flux. The strike point could also be shifted through different 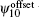without moving X and X2 points obviously. Figure 13 shows two constructed equilibria with 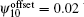and 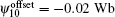. Maintaining the plasma shape and X & X2 point positions, the strike point shifts from the lower position to the upper position observably, while several PF currents (such as PF1–PF6) change dramatically. Normally, it is difficult to construct such configurations only by manual operation.

Fig. 13. The flux-linkage at the plasma boundary is set to zero. (a) The case of (case 3 in Table 4), (b) the case of (case 4 in Table 4).
4. Conclusion

In the TSC code, a shape constraint module has been developed. Comparing with the original method, it could quickly construct the divertor plasma equilibrium with the desired configuration. The plasma equilibrium with desired flux-linkage at the plasma boundary could be easily constructed, which could be used to scan the range of flux-linkage for the desired plasma configuration. Through setting a small offset flux at some special control point, the plasma configuration could make a small change which would reduce the cost of PF current dramatically. The designed results of DN, LSN, and QSF configurations prove the flexibility and practicability of this method, which has the potential for divertor configuration design in other tokamak.

Reference
1AlessandroBAngeloC 2005 IEEE Control Systems Magazine 25 44
2Jardin S CPomphrey NDelucia J 1986 J. Comput. Phys. 66 481
3Guo YXiao B JWu BLiu C Y 2012 Plasma Phys. Control. Fusion 54 085022
4WengP Dand the HT-7U team 2001 Fusion Eng. Des. 58�?9 827
5Liu LXiao B JHumphreys D ALuo Z PChen S L 2014 Fusion Eng. Des. 89 563
6Ariola MPironti A 2005 IEEE Control System 25 65
7Ryutov D D 2007 Phys. Plasma. 14 064502
8Ryutov D DCohen R HRognlien T DUmansky M V 2008 Phys. Plasma. 15 092501
9CalabròGCrisantiFRamogidaGet al.20137th IAEA Technical Meeting on Steady State Operation of Magnetic Fusion DevicesMay 14–17, 2013Aixen Provence, France
10Calabrò GXiao B JChen S Let al. 2015 Nuclear Fusion 55 083005
11Guo YXiao B JCalabr’o Get al.2014JPS Conf. Proc.101503510.7566/JPSCP.1.015035