Cite this Article
Shen Yang, Shen Hua, Liu Kai-Xin, Chen Pu, Zhang De-Liang. Three-dimensional detonation cellular structures in rectangular ducts using an improved CESE scheme. Chinese Physics B, 2016, 25(11): 114702  
Permissions
Three-dimensional detonation cellular structures in rectangular ducts using an improved CESE scheme
Shen Yang1, Shen Hua2, Liu Kai-Xin1, Chen Pu1, Zhang De-Liang3, †,
State Key Laboratory for Turbulence and Complex System, College of Engineering, Peking University, Beijing 100871, China
Department of Applied Mathematics and Computational Science, King Abdullah University of Science and Technology, Thuwal, Kingdom of Saudi Arabia
State Key Laboratory of High Temperature Gas Dynamics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China

 

† Corresponding author. E-mail: dlzhang@imech.ac.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 10732010 and 10972010).

Abstract
Abstract

The three-dimensional premixed H2-O2 detonation propagation in rectangular ducts is simulated using an in-house parallel detonation code based on the second-order space–time conservation element and solution element (CE/SE) scheme. The simulation reproduces three typical cellular structures by setting appropriate cross-sectional size and initial perturbation in square tubes. As the cross-sectional size decreases, critical cellular structures transforming the rectangular or diagonal mode into the spinning mode are obtained and discussed in the perspective of phase variation as well as decreasing of triple point lines. Furthermore, multiple cellular structures are observed through examples with typical aspect ratios. Utilizing the visualization of detailed three-dimensional structures, their formation mechanism is further analyzed.

PACS: 47.40.Rs;82.33.Vx;02.60.Cb
Keyword:CE/SE scheme;three-dimensional gaseous detonation;cellular pattern
1. Introduction

Detonation is a supersonic flow with chemical reactions. Since discovered in an experiment of flame propagation, it has been studied for over one hundred years. Nowadays the research on mechanism of detonation ignition and propagation, especially on structural analysis of cellular patterns, is still popular due to its importance in construction blasting, production security, military facilities,[1] and so on.

Limited by experimental equipment and technique, it is difficult to capture the details of detonation structures. As a result, smoked foil technique[2] and high-speed schlieren technique[3] were developed in 1960s to observe the detonation structure indirectly. White et al.[4] was the first to make a detailed experimental research on three-dimensional gas detonation. Strehlow[5–7] gave a well-documented description of detonation structure. In his papers, the structure of detonation cells had been described as an interaction of Mach configurations. Hanana et al.[8] experimentally obtained clear patterns recorded on the wall of square ducts. Through analysis, they considered that there were two kinds of stable cellular structures in three-dimensional cases: the diagonal mode and the rectangular mode. Lin et al.[9] improved the experimental set to study the critical structure in the transition process of the deflagration to detonation (DDT) under different boundary conditions.

Compared with experiments, numerical methods have advantages in providing global distribution of any variable at any time. A key problem of simulating the detonation is how to describe the chemical reaction in numerical method. Taki et al.[10] used a two-step kinetics model to analyze the structure of transverse wave. Oran et al.[11] proposed a detailed reaction model examining the cellular pattern of two-dimensional oxyhydrogen detonation. Besides, one-step kinetics model[12] and other simplified models[13] were also put forward in previous work. Sichel et al.[14] developed Taki’s model by introducing a parameter which reflected changes in gas composition, and promoted the computational precision a lot. In the early study, two-dimensional (2D) simulations were usually used to study the detonation cellular structures and there were thousands of literatures available. However, detonation was an intrinsically three-dimensional process. With the rapid development of computational fluid dynamics (CFD), three-dimensional simulations gradually became feasible. Williams et al.[15] adopted the one-step reaction model and numerically modeled three-dimensional structures in self-sustaining detonations. Their simulation started from a 2D periodic solution, and added a one-dimensional perturbation perpendicular to the motion of the initial 2D transverse waves. Tsuboi et al.[16,17] used a Harten–Yee non-monotone upstream-centered scheme to simulate three-dimensional hydrogen/air detonation and obtained the rectangular mode and diagonal mode. Deledicque et al.[18] also presented a detailed numerical study of three-dimensional structures in gaseous detonations using the one-step reaction model and a parallelized, unsplit, shock-capturing algorithm. Dou et al.[19,20] and Wang et al.[21,22] used the one-step kinetics model and the fifth order weighted essentially non oscillatory (WENO) scheme to simulate detonation propagation in square tubes. They found that the detonation wave in small size of square tubes could propagate spirally just as in round tubes, which was named as spinning mode. Additionally, Weng,[23] Ivanov,[24] Cai,[25] and Huang[26,27] also did a lot of simulation work with three-dimensional rectangular ducts and obtained similar results. However, to the best of the authors’ knowledge, most of previous work focusing on three-dimensional problems required a relatively high-order scheme and cost a plenty of computing resources.

In this paper, we employed the in-house parallel detonation code based on an improved three-dimensional space–time conservation element and solution element (CE/SE) scheme with second-order accuracy[28] to further study the three-dimensional cellular structures of detonation propagating in rectangular ducts. For the first time, we attained the cellular patterns with critical cross-sectional size as well as different aspect ratios.

2. Chemical reaction model and numerical method

Detonation is an extreme chemical reactive flow involving strong shocks. Therefore, to simulate the detonation process accurately, the following two aspects are crucial: (i) an appropriate chemical reaction model and (ii) a good shock capturing scheme. Currently, detailed chemical reaction models[11] are most close to the real situation, since elementary reactions actually occur during the detonation. However, it requires too many computational resources even for 2D cases, not to mention three-dimensional computation. To achieve an acceptable compromise between the solution accuracy and the computational time, we choose an improved two-step kinetic model,[14] in which the complex chemical reactions are simplified to an induction reaction and an exothermic reaction. Neglecting the influences of thermal conduction, viscosity, and mass diffusion, the detonation propagation can be described in three-dimensional Cartesian coordinate system by the reactive Euler equation

where U = (ρ, ρu, ρv, ρw,e, ρ α, ρ β)T, E = (ρu, ρu2 + p, ρuv, ρuw, (e + p)u, ρ αu, ρ βu)T, F = (ρv, ρuv, ρv2 + p, ρvw, (e + p)v, ρ αv, ρ βv)T, G = (ρw, ρuw, ρvw, ρw2 + p, (e + p)w, ρ αw, ρ βw)T, and S = (0, 0, 0, 0, 0, ωα, ωβ)T. U is the conservative vector. E, F, and G are the corresponding flux vectors in x, y, and z directions, respectively. S stands for the source term caused by chemical reactions. Variable e represents the total energy per unit volume, expressed as 

where Q is the H2–O2 reaction heat per unit volume and γ stands for the specific heat ratio. Dimensionless parameters α and β represent the reacting progress of induced reaction and exothermic reaction, respectively. Parameters ωα and ωβ in S represent the reaction rates of α and β, which are calculated as

The unit of temperature T, pressure P, and universal gas constant R0 are K, atm, and J/(mol· K), respectively. The analytical form and parameters determined for the induction period in Eq. (3) are based on a survey and study of existing models. Equation (4), measuring the process of heat releasing, is a generic Arrhenius form, in which the specific input parameters a, b, and c are determined by ensuring that they generally reproduced the properties of the full chemical kinetics model. It is deemed to provide the most accurate description of exothermic reaction in stoichiometric H2–O2 mixtures when a = 1.2 × 108, b = 8000, and c = 0.[14]

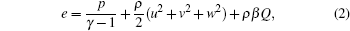
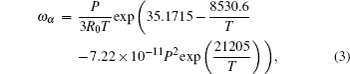
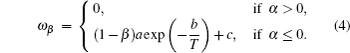
For shock capturing, we employ the CE/SE scheme,[29] which is a unique computational framework for solving hyperbolic equations. This numerical method takes time and space both as equal mathematical dimensions. Conservation elements (CEs) and solution elements (SEs) are defined appropriately to make local and global conservation law be strictly guaranteed. CE is a space–time control volume on which the conservation law is implemented. Meanwhile, SE is used to solve the fluxes involved in the discrete conservation law. The dissipation of the scheme can be efficiently controlled, because it is constructed based on a non-dissipative scheme.[29] As a result, it not only has a good shock capturing capacity, but also can be used to simulate acoustic waves.[30] In order to solve problems with complex boundary conditions as well as with a lower expense of computational resource, unstructured[31] and essentially conservative adaptive[32] definition of CEs can be also employed. But these improved schemes will lose some degree of global conservativeness. Moreover, dimension splitting method is not required for multi-dimensional cases, resulting in a genuinely multi-dimensional scheme.[28,33] These properties make CE/SE method be very efficient for detonation simulations. Up to now, it has already been successfully used for simulating gaseous detonation[34,35] and liquid-fueled two-phase detonation.[36,37]

Notably, the characteristic time scales for flow and chemical reactions may have several orders’ difference. To save CPU time, a decoupling method is used to handle the stiff source terms. That is to say, we first solve the flow field without considering chemical reactions and then integrate the source terms using sub-time step. According to the Gauss divergence theorem, the governing equation (1) without source terms can be written as

where H ≡ (U, E, F, G), S(V) is the boundary of an arbitrary close space-time region V, and ds = d σ · n with d σ and n being the volume and the unit outward normal vector of a boundary element of S(V), respectively. Integrating the second-order Taylor expansion on boundary of each CE, we can eventually get the relationship between current conservative vector and the one in next half time step as

with the m-th vector components of

Herein subscript parameters i, j, k, and superscript one n represent the sequence number of space-time mesh in x, y, z, and t direction, respectively. Symbols ±a and ∓a mean that when one of them makes a positive operator, the other must be negative. However, operator ±a, ±b, and ±c are independent of one another. Symbol ⋀ represents a new defined function through integration above, which expands as

where Nm can be Um, Em, Fm, or Gm. To get the value of , it requires to obtain the second derivative in spatial direction of the current space–time point (i, j, k, n) at first, namely ,,and . We can use first derivative value of the point in current time to estimate the second derivative and cross derivative next half step. Taking and as an example, the differential formula is

Then the value of can be obtained using Eq. (6). Finally, similarly with first-order Taylor expansion,[28] the continuity of variables in SEs at the junction point is made use to get the x, y, z directional derivatives of conservative vector in next time step.

3. Results and discussion

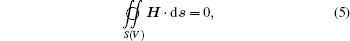
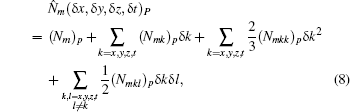
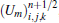
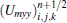
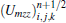
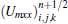
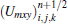
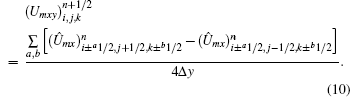
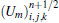
Numerous factors, including the size and aspect ratio of cross-section, the initial perturbation, the reaction model and so on, exert a coupling effect on detonation structures in a rectangular duct. We focus on the effect of the size and aspect ratio of cross-section (AR) herein. Although the cellular structures in square tubes have been comprehensively studied before, we carry out similar simulations both as a code validation and as baselines for comparison. The settings of 14 total cases are listed in Table 1. There are five things to note. (i) At least 50 grid points are guaranteed for one cellular width to ensure the accuracy of simulation results. We have tried beforehand the simulation with grid resolution of 10, 25, and 50 points per millimeter (pts./mm). After comparison of the cellular patterns, we concluded that 25 pts./mm is enough for examples with cross-sectional size greater than 2 mm, while it had better be 50 pts./mm when cross-sectional size equals to 1 mm. (ii) It needs to lengthen the computational domain to 160 mm when the cross-sectional size reduced to 2 mm or 1 mm, because detonation structure at first 80 mm in these cases is not always stable. (iii) All the initial perturbations are only given at first 30 time steps to trigger transverse waves. (iv) Each example takes 8 CPU cores in parallel running. (v) In all cases, high pressure is initially implemented on the left 5% part of the computational domain (P = 45 atm and T = 298 K) and the rest part is filled with H2–O2 mixtures of normal temperature and pressure (P = 1 atm and T = 298 K). Additionally, reflective boundary condition is performed for all the side walls, the left wall of CPU 1 and the right wall of CPU 8.

Table 1.

Simulation parameters in different cases.

.
3.1. Influences of cross-sectional size

In the cases with square cross-sections, the diagonal mode and the rectangular mode are observed in Cases 1 and 2 with relatively large cross-section size, and the spinning mode is obtained in Cases 5 and 6 with very small size, as shown in Figs. 1(a), 1(b), 1(e), 1(f), 2(a), 2(b), 2(e), and 2(f). In the propagation process of Case 1 or 2, the shock front and the transverse waves (TW) intersect at a set number of triple point lines (TL), the trajectory of which will form fish-scale shaped cellular pattern on walls of the duct, as shown in Figs. 2(a) and 2(b). The shock front is divided by TLs into several protruding Mach stems (MS) and incident shocks (IS). Adjacent TLs impact and separate generating new MS, meanwhile old ones damping to IS. In diagonal mode, each of two groups of TLs forms enclosed rectangles, which are orthogonal to each other and manage about 45 degrees on lateral walls of the duct. Both rectangles keep centrosymmetric and the whole structure has four symmetric axes. Meanwhile, TLs in rectangular mode are parallel to the wall and show transverse lines of high pressure, called slapping waves, on the surface in each cycle. In Cases 5 and 6, the simulation results show two similar types of spinning structures, one spinning clockwise and the other spinning counterclockwise, depending on types of initial perturbation. In this condition, only two perpendicular TLs exist. Comparing with situation in Case 2, these two TLs have approximately π/4 radian of phase difference, and lose all the symmetry. Figure 2(e) or 2(f) shows that a strip with high pressure can be observed spinning along the wall. The thickness of the pattern on each side wall is not uniform, because the TL parallel to the wall gradually leaves away from the surface. This is another type of influence by the slapping wave.

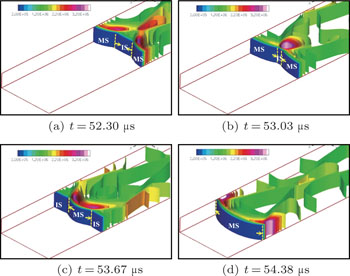
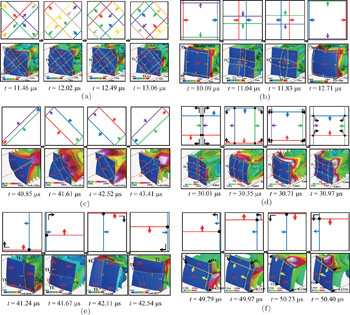Fig. 1. Pressure isosurfaces and motion of TLs during about one period in (a) Case 1, (b) Case 2, (b) Case 3, (d) the middle domain of Case 4, (e) Case 5, and (f) Case 6.
Fig. 2. Distribution of maximum pressure histories on expansion of the lateral walls in (a) Case 1, (b) Case 2, (c) Case 3, (d) the middle domain of Case 4 with typical y–z slices, (e) Case 5, and (f) Case 6.

Logically, critical structures appear in Cases 3 and 4 with medium cross-section size. In Case 3 with initially diagonal perturbation, the elementary cells shown in Fig. 2(c) are the same as 1/4 fusiform shape partitioned along central x–y and x–z planes in Fig. 2(a). Comparing motion of TLs shown in Fig. 1(c) with typical diagonal mode, the critical patterns have only one group of TLs forming an enclosed rectangle on the shock front. This kind of structure loses axisymmetry but keeps centrosymmetric, in which two couples of parallel TLs sustain a phase difference of π/4 radian. As for Case 4 with initially rectangular perturbation, two couples of TLs gradually accumulate π/8 radian of phase difference at the middle of computational domain, as shown in Fig. 1(d). It is evident that the cellular structure in Case 4 is swept by each two groups of TLs in Cases 5 and 6 with π/2 radian of phase difference. In our observation of maximum pressure histories (MPHs) on section x–y and x–z in Fig. 2(d), this transition structure has bright oblique stripes with uneven thickness, more like structures in Figs. 2(e) and 2(f) other than normal rectangular mode. If we examine the MPHs on y–z slices, spinning motion of four points intersected by TLs can be observed clearly. Therefore, it can be also named as quadruple spinning. However, this transition structure will not keep all along but eventually turn into single spinning.

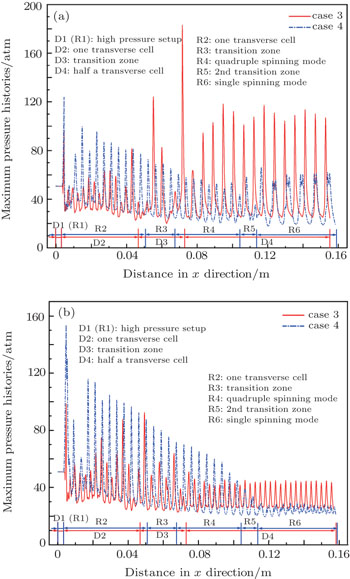
Furthermore, we extract the data of MPHs along the central and angular lines in x direction and make the diagram displayed in Fig. 3. In regions D2 and R2, both two propagation modes are forced to have one transverse cell. Correspondingly, the peak value of pressure in each cycle is unstable. In regions D3 and R3, the detonation structure is firstly in the process of transition. In Case 3, one group of TLs gradually disappears in about 5–7 cycles, while two couples of TLs in Case 4 accumulate phase difference to transform typical rectangular patterns into quadruple spinning. Finally in region D4 for the diagonal mode, pressure histories almost have the same amplitudes with an enclosed rectangle of TLs holding at π/4 radian phase difference. That means that the detonation structure keeps self-sustaining. However in the rectangular mode, quadruple spinning is not as stable as structures in Case 3, since it needs a relatively high energy to keep this propagation style. As seen in Fig. 3, the envelope curve of pressure histories has a trend of decreasing while temporarily keeping typical rectangular and quadruple spinning mode. It lasts until to the second transition region R5, in which the pressure close to shock front reaches a critical value. In this transition zone, cellular patterns gradually merge together and TL number decreases. Ultimately in region R6, the detonation structures change to steady single spinning, being the same as patterns in Case 6.

Fig. 3. Comparison of MPHs along the central line (a) and angular line (b) between Cases 3 and 4.

Generally speaking, when the size of cross-section is big enough, it will form diagonal or rectangular pattern, depending on types of initial perturbation. Otherwise, when the size of cross-section is very small, the detonation structures will finally convert into spinning patterns, however we change the other conditions. Additionally, critical structures also exist while the diagonal or rectangular mode is transformed into the spinning mode. It is the process with accumulation of phase difference and decreasing of TLs. Comparing with the rectangular mode, the diagonal one is more difficult to be transformed into the spinning mode, since TLs in this condition originally move along the diagonal line, different from spinning structures.

3.2. Influences of cross-sectional aspect ratio

In different propagation modes, the AR makes different influences on cellular structures. Firstly, we assess the effect with the cell size equal to 4 mm. Cases 1, 7, and 9 with AR ranging from 1 to 3 are carried out to study multiple cellular structures in the diagonal mode. When the length in one transverse direction of square tubes is stretched integer times, detonation cells generally duplicate the same number, as in Case 9. But if carefully examining the cellular structure of Case 7 in Fig. 4(a), we find that even though the size on x–z sides does not change, the number of cells also turns from one in Case 1 to a half. Correspondingly, the cellular patterns on z–y sides decrease to 1.5 transverse cells. Figure 5(a) clearly shows the distribution of MPHs on several y–z slices in half a cycle. Those high pressure areas are swept by TLs. One of the most remarkable things is that multiple cellular structures on section A–A, B–B, and C–C consist of elementary cells as in Case 3 with adjacent units keeping opposite phases, rather than structures shown in Fig. 5(b) or 5(c). In essence, imaginary style 5(c) is based on 5(b). Their relationship is similar to Case 3 and Case 1, which to form is determined by the cross-sectional size. The reason for the final cellular structure presenting like Fig. 5(a) comes down to the preservation and loss of symmetry. Specifically, the elementary structures in Figs. 5(b) and 5(c) remain axisymmetry but lose centrosymmetry, and the other way around in style 5(a). It is considered that keeping axisymmetric is more difficult than remaining centrosymmetry, which can be proved by critical situation in Case 3. Furthermore, multiple structures in Case 9 are also not appropriate for Case 7, because its length of the longer side is relatively small. Therefore, it is not surprising for cellular patterns in Case 7 being the compressing version of elementary structures in Case 9.

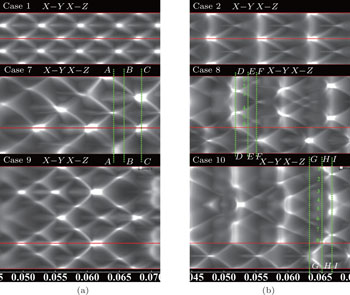Fig. 4. Cellular patterns on the lateral walls with typical ARs in (a) Cases 1, 7, and 9, as well as in (b) Cases 2, 8, and 10.
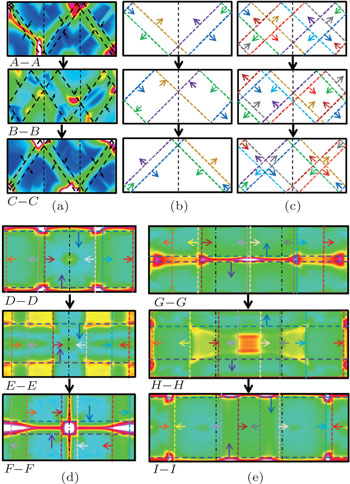Fig. 5. Distribution of MPHs with motion of TLs on y–z slices in Case 7 with (a) simulation results, and (b) one or (c) another kind of imaginary structures, as well as (d) in Case 8 and (e) Case 10.

Similarly, Cases 2, 8, and 10 are used to study multiple cellular structures in the rectangular mode. For all the cases, the number of cells on sides of the ducts does not change like Case 7, as shown in Fig. 4(b). It has been discussed above that accumulation of phase difference and decreasing of TLs eventually come to structure of Case 3 in the diagonal mode, but to the quadruple spinning of Case 4 in the rectangular mode. Consequently, it is impossible to form a half cell in rectangular motion of TLs. In addition, TLs in a rectangular elementary cell are parallel to the duct wall. That is to say, in multiple structures TLs parallel to the longer sides must be linked to a whole line to keep steady, resulting in keeping the same phase along z direction. If observing the surface on the longer sides of the duct, we will find a linked slapping wave in each cycle. Figures 5(d) and 5(e) clearly show distribution of MPHs on several y–z slices in Cases 8 and 10. On section E–E and H–H, we can find that the associated TL is not entirely straight, of which the middle part has a delay comparing with the edge. But this kind of difference will not accumulate, as shown in section D–D, F–F and G–G, I–I. Another thing worth noting is that the number of TLs along y direction is not a process of linear growth with AR increasing, nor the phase of TLs will present the elementary structures as in Case 2. But in general, positions of TLs keep centrosymmetric as well as axisymmetric.

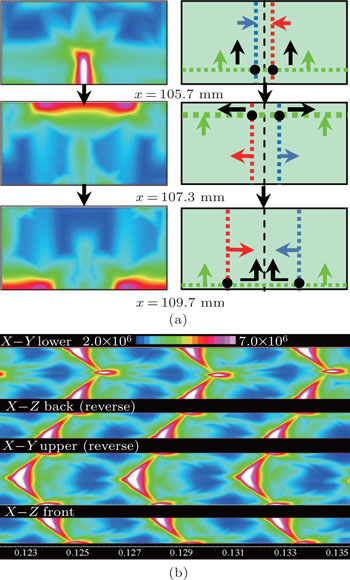While simulating with the cell size of 1 mm, the effect of ARs differs a little from examples above. A case study of initially diagonal perturbation and AR = 2 (Case 11) is shown in Fig. 6. Comparing with Figs. 1(d) and 1(e), we find that the cellular structures in this case consist of two elementary cells in Case 5 with opposite spinning directions, which appear also similar with the upper half part of patterns in Case 4. In this condition, each of two TLs parallel to shorter sides just moves twice as long as that parallel to longer sides. However, if taking these two TLs as a whole, their motion cycle is the same as the long TL. This type of detonation structure forms at the first quarter of the computational domain and keep steady all the time.

Fig. 6. Cellular patterns on the surface in Case 11, including (a) y–z slices and (b) expansion of lateral walls.

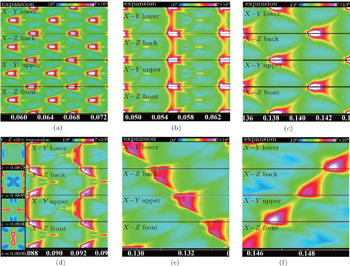
On the other hand, results in Case 12 with initially rectangular perturbation have something different. Observing the cellular patterns in Fig. 7, the detonation structures become similar to those with initially diagonal perturbation in the middle area of the domain. However, the cellular patterns on lower or upper side in this case just correspond to patterns on upper or lower one in Case 11. That is to say, intersection of TLs in these two cases moves in opposite spinning directions. When the detonation propagates to the third quarter of the domain, the cellular patterns will change to the type shown in Fig. 7(b). It looks like the structure of single spinning, but actually with certain difference. After a careful examination of the MPHs on y–z section, we find that TLs in this example spin neither as Case 5 nor as Case 6, but move along the path of symbol ∞. Figure 8 show the distribution of MPHs on y–z slices in about one cycle, in which two directions of ∞ shaped trajectory are clearly displayed.

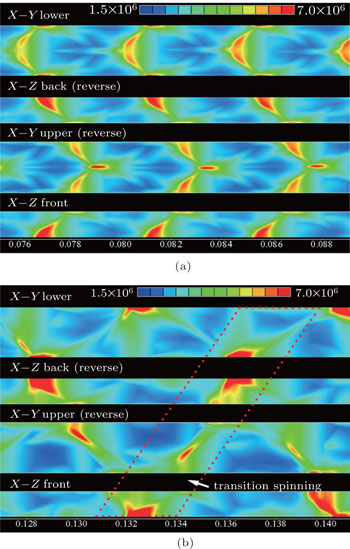Fig. 7. Cellular pattern on x–y and x–z sides in Case 12 with x ranging from 0.075 m to 0.089 m (a), and from 0.127 m to 0.141 m (b).
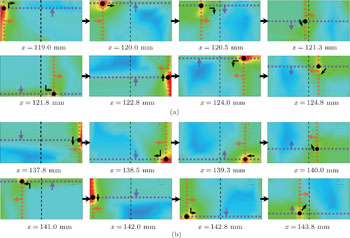Fig. 8. Two kinds of ∞ shaped trajectory of the cellular patterns on y–z slices in Case 12. (a) One direction of ∞ shaped trajectory. (b) The other direction of ∞ shaped trajectory.

The most remarkable difference between structures in Figs. 6 and 8 is the number of short TLs. In Case 12 with initially rectangular perturbation, TLs moving along y direction will eventually merge to only one line. Furthermore, as discussed in Case 11, this unique TL on shorter sides of the duct moves twice as long as the long TL does, which finally forms the ∞ shaped motion style. Another thing we are interested in is how these two motion styles displayed in Fig. 8 make a mutual transformation. Through observing the details of the whole structures on y–z slices along x direction, it is confirmed that one cycle of transition spinning exists between these two types, as shown in Fig. 7(b). This means at some special time, the motion cycle of the short TL will be equal to the long line, as in Case 5 or 6. The most obvious difference between zone before and after on the lateral walls is that the strips on x–z sides stretch in orthogonal directions.

As expected, if the AR becomes big enough, the detonation structure will degenerate to the 2D situation. Take simulation results in Case 14 as an example, in which we set AR = 4:1 with initially rectangular perturbation, as shown in Fig. 9. On the shorter side of the duct, MPHs almost do not change along z direction, and cellular patterns on the longer sides of the duct are similar to results in 2D simulations. Therefore, there are only two TLs moving along y direction with good symmetry. Additionally, Case 13 with AR = 3 is the critical situation, in which the structures start as in Fig. 9 and end at Fig. 8, never forming patterns of double spinning shown in Fig. 7(a).

Fig. 9. Pressure isosurfaces in about half a cycle in Case 14.
4. Conclusion

An in-house parallel detonation code based on the CE/SE scheme with second-order Taylor expansion as well as two-step kinetic model is used to simulate the three-dimensional detonation in rectangular ducts with premixed H2–O2 atmosphere. We chiefly obtain three well-understood types of propagation mode as well as critical structures through typical examples in square tubes, and then examine the influence of AR on detonation cellular structures in the rectangular, diagonal and spinning mode. Ultimately, the simulation reveals that: (i) the process of the rectangular or diagonal mode transforming into the spinning mode occurs with phase variation as well as decreasing of TLs; (ii) multiple cellular structures will generally consist of elementary cells in square tubes with certain phase difference or periodic inequality, or degenerate to the 2D situation when assigned a high value of AR. Based on our results, we conclude that quantitative change in size or aspect ratio of cross-section will finally make qualitative differences on the three-dimensional detonation cellular structures.

Reference
1Roy G DFrolov S MBorisov A ANetzer D W 2004 Prog. Energ. Combust. 30 545
2Denisov Y NTroshin Y1959Proc. Acad. Sci. USSR: Phys. Chem. Sec.125217
3Bennett F D 1962 Phys. Fluids 5 891
4White D RCary K H 1963 Phys. Fluids 6 749
5Strehlow R A 1968 Combust. Flame 12 81
6Strehlow R A1969Astronaut. Acta14539
7Strehlow R A1970Astronaut. Acta15345
8Hanana MLefebvre M Hvan Tiggelen P J 2001 Shock Waves 11 77
9Lin WZhou JFan X HLin Z Y 2015 Chin. Phys. 24 014701
10Taki SFujiwara T 1978 AIAA 16 73
11Oran E SWeber J WStefaniw E ILefebvre M HAnderson J D 1998 Combust. Flame 113 147
12Zhang Z CJohn Yu S THao HChang S C2001AIAA 2001-047610.2514/6.2001-476
13Montgomery C JCannon S MMawid M ASekar B2002AIAA 2002-033610.2514/6.2002-336
14Sichel MTonello N AOran E SJones D A 2002 Proc. Roy. Soc. Lond. 458 49
15Williams D NBauwens LOran E S 1996 Symp. Combust. 26 2991
16Tsuboi NKatoh SHayashi A K 2002 P. Combust. Inst. 29 2783
17Tsuboi NHayashi A K 2007 P. Combust. Inst. 31 2389
18Deledicque VPapalexandris M V 2006 Combust. Flame 144 821
19Dou H STsai H MKhoo B CQiu J X 2008 Combust. Flame 154 644
20Dou H SKhoo B C 2010 Shock Waves 20 163
21Wang CShu C WHan W HNing J G 2013 Combust. Flame 160 447
22Wang CLi PZhen GDon W S 2016 Comput. Fluids 55 351
23Weng C SGore J P 2005 Acta Mech. Sin. 21 32
24Ivanov M FKiverin A DYakovenko I SLiberman M A 2013 Int. J. Hydrogen Energ. 38 16427
25Cai X DLiang J HDeiterding RChe Y GLin Z Y 2016 Int. J. Hydrogen Energ. 41 3222
26Huang YJi HLian F STang H 2012 Chin. Phys. Lett. 29 114701
27Huang YJi HLian F STang H 2014 Shock Waves 24 375
28Shen HLiu K XZhang D L 2011 Chin. Phys. Lett. 28 124
29Chang S C 1995 J. Comput. Phys. 119 295
30Wang X YChang S CJorgenson P C E2000AIAA 2000-047410.2514/6.2000-474
31Fu ZLiu K X 2012 Chin. Phys. 21 040202
32Fu ZLiu K XLuo N 2014 Chin. Phys. 23 020202
33Chang S CWang X YChow C Y 1999 J. Comput. Phys. 156 89
34Zhang MJohn Yu S TChang S C2004AIAA 2004-007510.2514/6.2004-75
35Wang GZhang D LLiu K X 2007 Chin. Phys. Lett. 24 3563
36Wang GZhang D LLiu K XWang J T 2010 Comput. Fluids 39 168
37Shen HWang GLiu K XZhang D L 2012 Int. J. Nonlinear Sci. Numer. Simul. 13 177