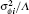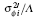† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 61308082).
When building an experimental platform for light propagation along an inhomogeneous turbulent path, it is very essential to set up the reasonable distribution of phase screen. Based on multi-layered model of phase screen, an iterative optimization algorithm of phase screen position is given in this paper. Thereafter, the optimal position of phase screens is calculated under the Hufnagel–Valley5/7 and Hefei-day turbulence profile. The results show that the positions of phase screen calculated by the iterative algorithm can fit well with the turbulence profile rather than mechanically placed phase screens at equal distance. Compared with the uniform distribution of phase screens position, the residual phase error of the iterative algorithm decreases very significantly. The similarity degree between them is minimal when number of layers is equal to two.
Atmospheric optical communication has been receiving considerable attention recently for providing secure, low-cost, rapidly deployable, dynamic data transmission at very high rates.[1] However, owing to inhomogeneity in the temperature and pressure of the atmosphere, the refractive index varies along the optical path, which in turn leads to angle-of-arrival fluctuations, intensity fluctuations, and beam broadening.[2,3] Thus, these deleterious effects of turbulence severely limit the performance of the laser communication system.
At present, a method for modeling laser beam propagation in a turbulent atmosphere by using thin phase screens along the propagation path has been studied extensively.[4–6] In the laboratory, this method can be served as a guidance for building an experimental platform for light propagation along an inhomogeneous turbulent path. The most commonly used equipment of simulating atmospheric turbulence is based on liquid-crystal spatial light modulators (SLM) and rotating glass plate, which act as the phase screen. Considering the high expenses of these experimental device, it would not be possible to set up too many phase screens in the experiment. Meanwhile, when laser beam propagation along the nearly horizontal path where the atmospheric structure constant of the refractive index is approximately equal to be constant, discrete phase screens are always distributed uniformly. But with the consideration of the vertical and sloping paths through a turbulent atmosphere, the strength of turbulence is a function of height, wind speed and meteorological parameters. If the uniform distribution of phase screens is still used in this case, the effects of atmospheric turbulence could not be simulated accurately. So a reasonable distribution of phase screens becomes very necessary. Schmidt et al. explored the effective position distribution of phase screens to avoid unnecessary complexity in the laboratory setup.[7] His method is based on the situation that one phase screen is located in the transmitter plane and the other half way to the receiver. Phillips et al. introduced different schemes of phase screen distribution in order to achieve certain values of the Rytov variance.[8] Qian et al. outlined three different methods: uniformly distributed phase screen, equivalent Rytov index-interval phase screen and equivalent Fried parameter-interval phase screen.[9] In addition, Fusco et al. presented that small number of equivalent layers (2 or 3) is required to obtain an accurate restitution of the phase in a large field of view.[10] But both efforts do not solve the problem of the position distribution of phase screens along an inhomogeneous turbulent path systematically, which means that a suitable mathematical physical model has not been put forward to solve it. Moreover, personal subjectivity in choosing the position and number of phase screens may increase uncertainty of experimental results. In our case, a number of phase screens are placed along 11 meters of light propagation path in the experimental platform to simulate the effect of atmospheric turbulence within 10 km. Although a large number of phase screens are applied in the numerical simulation, it cannot be achieved in the laboratory limited by experimental funds. So it is very necessary to explore the phase screen distribution with minimum condition along an inhomogeneous turbulent path.
In this paper, based on the multilayer model of atmospheric turbulence, an iterative optimization algorithm of phase screen position is investigated. Meanwhile, under condition of the Hufnagel–Valley5/7 and Hefei-day atmospheric turbulence profile model, the optimal distribution of phase screens and the boundary of atmospheric discrete layers are calculated respectively. The minimum condition of phase screen distribution are also introduced by the analysis of similarity degree.
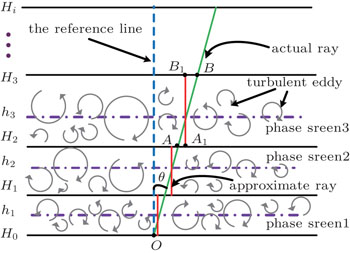
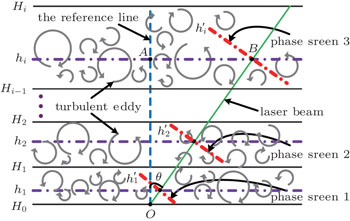
The atmospheric turbulence is modeled as a series of thin phase screens, as shown in Fig.
The angle θ between the actual laser beam (green line) and the approximate one (red line) is very small. Thus we assume that the strength of the turbulence varies little along the horizontal direction. The optical path difference (OPD) between them is given by[11]
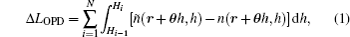
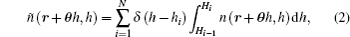
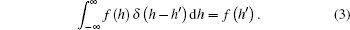
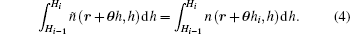

The relationship between phase difference Δϕ and optical path difference ΔLOPD can be described as
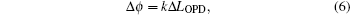
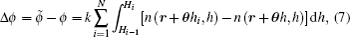
From Eq. (
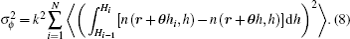
Under the Kolmogorov model, the most commonly used length scale is the Fried parameter r0. The 2D phase structure function in this case is

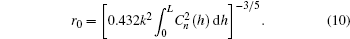
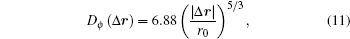
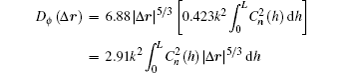
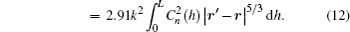
Consolidating Eqs. (
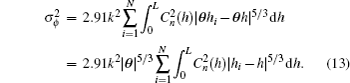
In order to assure that the effects of discrete phase screens match those of the atmospheric turbulence in reality best, the variance of residual phase error 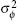
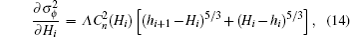
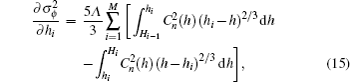
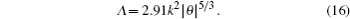

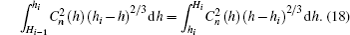
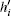
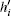
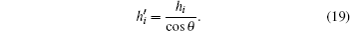
In order to better illustrate the principles of the iterative algorithm, we describe the basic steps as follows:
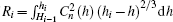
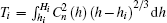
The parameter 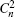
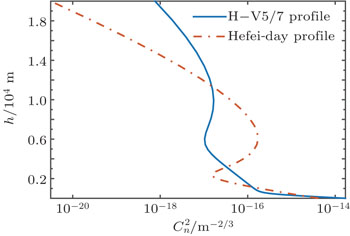
The H–V5/7 profile is given by[12]
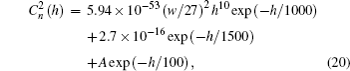
The Hefei-day profile is the observational results of the atmospheric structure parameter in Hefei (China), which is defined by[13]
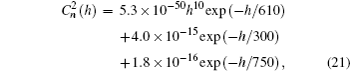
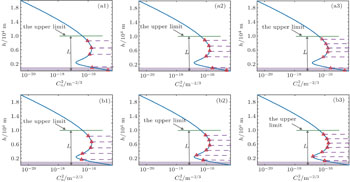
In this section, numerical calculations are carried out for the positions of phase screens and boundaries of each layer of atmosphere under H–V5/7 and Hefei-day profile. In the process of calculations, we use the ground H0 = 0, the propagation distance L = 10 km, the upper limit HN = L, and number of layers N = 1,2,3,…,7.
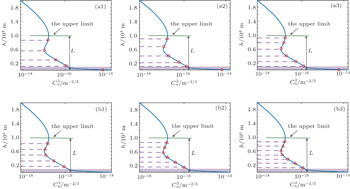
Figures
Similarly, figure
Tables
| Table 1. The thickness of each layer and positions of phase screens (PS) for the H–V5/7 profile. . |
| Table 2. The thickness of each layer and positions of phase screens (PS) for the Hefei-day profile. . |
According to Eq. (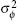
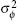
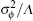
It can be seen that 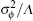
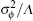
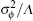
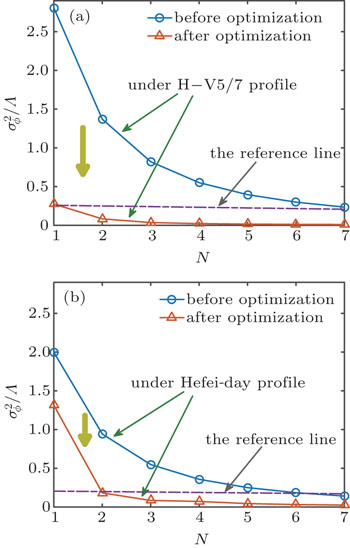
To describe the total ratio of error reduction after the iterative optimization algorithm is applied, we define the weighted mean of error reduction τ
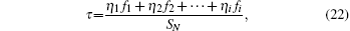
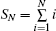

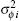
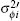
| Table 3. The single and total ratio of error reduction after optimization for the H–V5/7 profile. . |
As shown in Tables 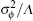
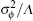
| Table 4. The single and total ratio of error reduction after optimization for the Hefei-day profile. . |
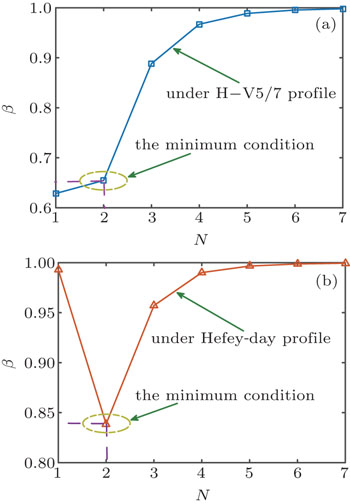
The minimum condition means that a least number of equivalent layers is required to obtain enough accuracy of multi-layered model of phase screen in the laboratory. In order to find out the minimum condition through the difference between the lines before and after optimization in Fig.
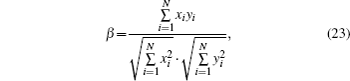
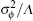
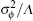
The smaller the values of the similarity degree β is, the larger deviation between γi and κi is. Figure 
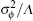
The iterative optimization algorithm of phase screen position along an inhomogeneous turbulent path has been discussed. For the H–V5/7 and Hefei-day profile, our results give the values of specific locations of phase screens, which can be used in a specific experiment. It is important to note that this iterative optimization algorithm is not limited by a certain turbulence profile. Compared with the uniform distribution of phase screens, the positions of phase screen calculated by the iterative algorithm can fit well with the specific turbulence profile. The variance of residual phase error was obviously decreased after the iterative optimization algorithm is used. The total ratio of error reduction after optimization is about 22.1 and 5.51 respectively for H–V5/7 and Hefei-day profile. Moreover, the minimum condition that the number of layers N is equal to two is also analyzed. When the scheme of this condition is used, the similarity degree of the curve before and after optimization is minimal.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 |