† Corresponding author. E-mail:
Project supported by the National Nature Science Foundation of China (Grant No. 11504318).
We propose a versatile electrostatic trap scheme using several charged spherical electrodes and a bias electric field. We first give the two-ball scheme and derive the analytical solution of the electric field. In order to make a comparison, we also give the numerical solution calculated by the finite element software (Ansoft Maxwell). Considering the loading of cold polar molecules into the trap, we give the three-ball scheme. We first give the analytical and numerical solutions of the distribution of the electric field. Then we simulate the dynamic process of the loading and trapping cold molecules using the classical Monte Carlo method. We analyze the influence of the velocity of the incident molecular beam and the loading time on the loading efficiency. After that, we give the temperature of the trapped cold molecules. Our study shows that the loading efficiency can reach 82%, and the corresponding temperature of the trapped molecules is about 24.6 mK. At last, we show that the single well divides into two ones by increasing the bias electric field or decreasing the voltages applied to the spherical electrodes.
Cold molecules play an important role in basic physics and advanced technology. Cold molecules have lots of applications, such as high-resolution spectroscopy[1] and precision measurements,[2] cold collisions and cold chemistry,[3–5] quantum computing and quantum information processing,[6] and so on. Manipulation of cold polar molecules using the interaction between their electric dipole moments with an inhomogeneous electric field has obtained great achievements in recent years. In 2000, Meijer’s group trapped the ND3 molecules in the weak-field-seeking (WFS) state using an electrostatic well for the first time. After that, they succeed in trapping OH radical[7] and metastable CO molecules[8] using the same setup. In 2005, Rempe group trapped ND3 molecules in a continuously operated electrostatic trap.[9] In 2007, Kleinert et al. confined ultracold polar NaCs molecules using thin-wire electrostatic trap.[10] In 2009, Meijer’s group reported the trapping of carbon monoxide molecules on a chip using direct loading from a supersonic beam.[11] Yin’s group has also made considerable contributions to this area.[12–18] In 2013, Wang et al. proposed an electrostatic trap with three-dimensional (3D) optical access using two charged spherical electrodes.[15] Though the optically accessible trap can catch cold polar molecules in the WFS state, it still has some shortcomings. The main drawbacks are as follows. First, the loading efficiency is only 14%. Second, as is demonstrated, double-well trap has lots of important applications in atom and molecule optics.[19–22] While in this scheme, only single trap can be formed. Last but not least, the analytical solutions for the distribution of the electric field in the ultimate scheme are not given. Though in 2015, they proposed an improved scheme,[16] the last two shortcomings still need to be overcome.
To solve these problems, we propose a versatile electrostatic trap with open optical access for cold polar molecules in the WFS state using several spherical electrodes and a bias electric field. We not only derive the analytical solution of the electric field, but also give the numerical solution calculated by the finite element software. We demonstrate the feasibility of our trap scheme using classical Monte Carlo simulations. In Section 2, we first give the two-ball scheme. In Section 3, considering the load of the cold polar molecules, we give the three-ball scheme, and give the analytical solution and numerical solution of the electric field. We perform the classical Monte Carlo simulations to better understand the dynamic behavior of cold molecules in the loading and trapping processes. We show that the single well can be divided into two halves by continuously increasing the intensity of the bias electrode field.
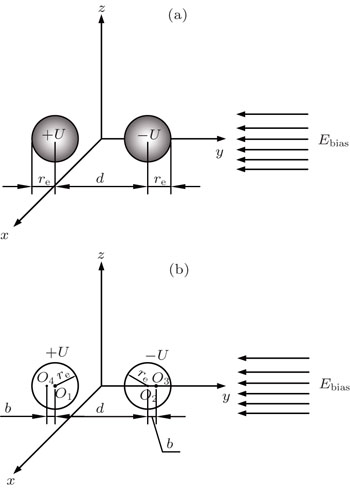
The two-ball scheme is composed of two charged spherical electrodes with a radius of re, as shown in Fig.
According to the method of image charges, as shown in Fig. 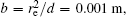
The voltages applied to the electrodes are actually achievable at current stage.[16,23–28] The charges Q1, Q2, Q3, Q4 at the points O1, O2, O3, O4 respectively are 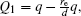
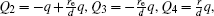
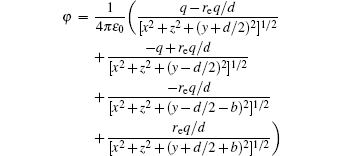
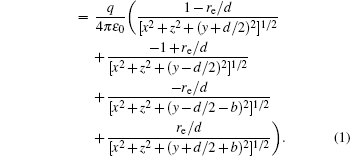
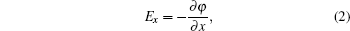
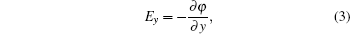
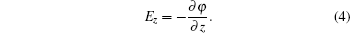

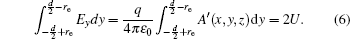
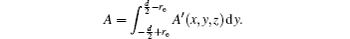
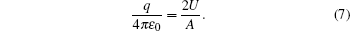

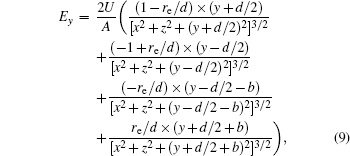


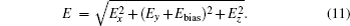
With Eqs. (
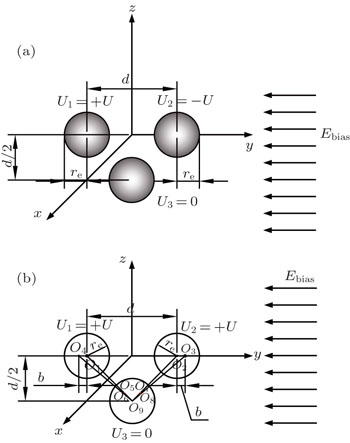
In this section, we add a spherical electrode to our double-ball scheme in –z axis to realize the efficient loading and trapping of cold polar molecules. The added sphere is the same size as the above mentioned two spheres. The coordinate of the centre of the sphere is (0, 0, –d/2). The voltages applied to the three balls are U1, U2, and U3, respectively. In the process of trapping, U3 = 0, U1 = U, U2 = −U, and Ebias ≠ 0, while in the process of loading, U3 = 0, U1 = U2 = U, and Ebias = 0. Here we use the results of the two-ball scheme to simplify the calculation. We use re = 0.004 m, d = 0.016 m, 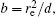
The point charges
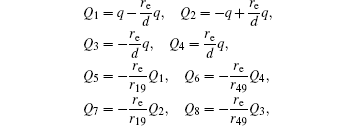
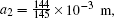
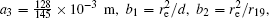

According to the Poisson equation and image charge method, we can get the electric potential by
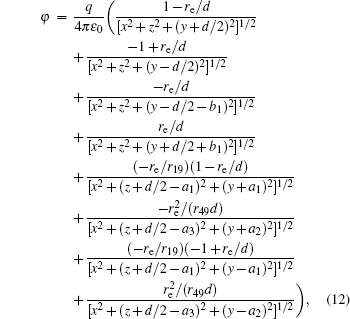



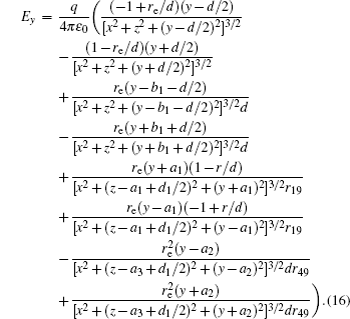
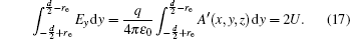
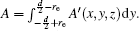

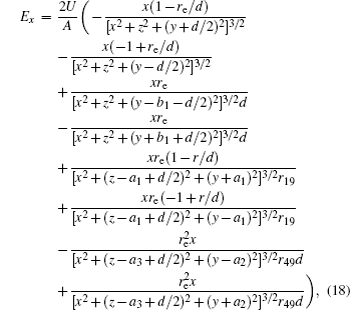
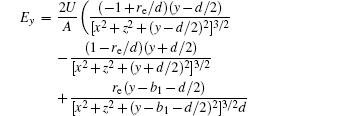
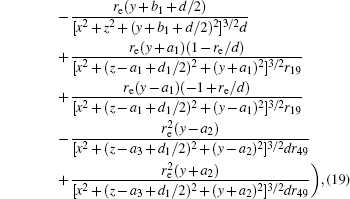
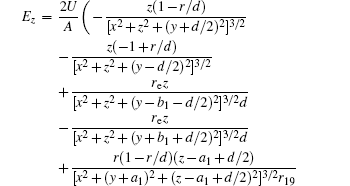
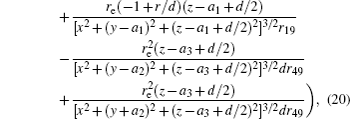
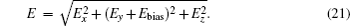
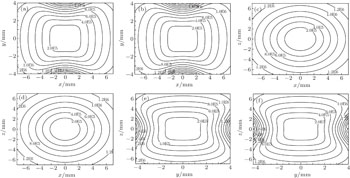
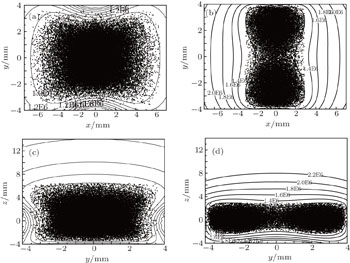
Similar to the two-ball scheme, we compare the contour distributions of the electric field calculated with Eqs. (
We calculate the spatial distribution of the electrostatic field generated by our charged-ball layout and its Stark trapping potential for ND3 molecules, and analyze the effective potential-well depth.
The ND3 molecule in the state |J,K,M〉 = |1, 1, −1〉 has a relatively large electric dipole moment (1.5 Debye). When a ND3 molecule moves in an inhomogeneous electric field, it will experience an electric dipole gradient force, and the corresponding interaction potential will be given respectively by the first-order Stark potential
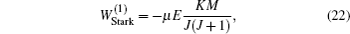
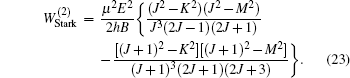
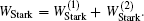
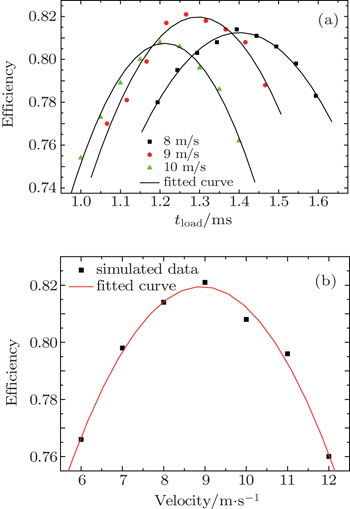
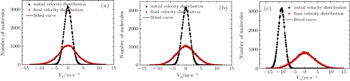
In our simulations, the number of simulated molecules is 105. The initial spatial distributions and velocity profiles of incident pulsed ND3 molecular beam are both Gaussian ones, and the transverse (x, y) and longitudinal (z) spatial sizes are 4 and 8 mm, respectively. The center velocity of cold molecular beam in the x and y directions both are 0 m/s, and the corresponding full width at half maximum (FWHM) of the velocity distributions in x, y, and z directions are all 3 m/s. The simulated conditions are actually achievable at current stage.[30–32] Here, tload is the time when we change the loading electric field to the trapping one.
Figure
Figure
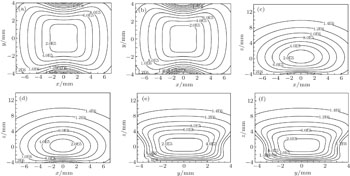
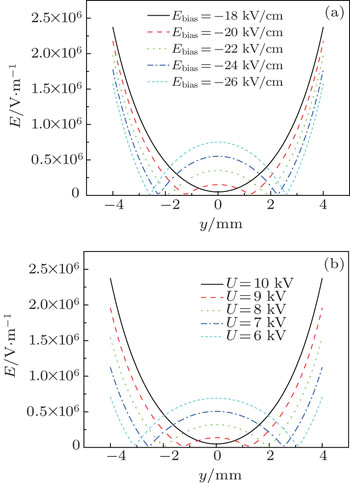
Our layout can easily realize the transition from single well to double wells by changing the values of the bias electric field and the voltages applied to the ball electrodes. When the intensity of bias field increases, the single well splits into two identical halves, shown in Fig.
First, we keep U = 10 kV unchanged and analyse how the intensity of electric field affect the formation of double wells, shown in Fig.
We have proposed a novel scheme for trapping cold WFS molecules by using several charged balls and a bias electric field. We analytically and numerically calculate the spatial distributions of the electrostatic field generated by our charged-ball layout and its Stark trapping potential for ND3 molecules. The Monte Carlo simulations for the loading and trapping processes of cold ND3 molecules are performed to study the dependences of the loading efficiency on both the loading time and the initial velocity of the incident molecular beam. The results show that the loading efficiency of our trapping scheme can reach up to 82% when the initial velocity of the molecular beam is 9 m/s, and the corresponding optimal loading time is 1.2660 ms. We also study the transition from single well to double wells by changing the value of the voltage or the intensity of bias electric field. This is of great importance to the interferometric study of molecular matter waves. With cold molecules trapped in an electrostatic well up to seconds, we can study the lifetimes of the electronic or vibrational excited states.[33,34] Trapped polar molecules also hold promise for use in quantum information systems.[35]
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 |