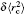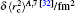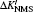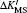Isotope shifts (ISs) of the lithium isotopes and other few-electron systems (such as helium, beryllium, boron, carbon, Li-like ions, etc.) have recently received more and more attention both theoretically and experimentally because of their important applications in atomic physics.^[1–3] There are mainly three reasons as follows. First, these few-electron systems could be used to test the fundamental atomic theory with high accuracy. Second, information about nuclear spins, magnetic dipole moments, electric quadrupole moments, hyperfine structures, and nuclear charge radii can be extracted from the high-precision measurement of ISs. Moreover, there are a certain number of halo nuclei^[4–6] in the light element isotopes. The ISs determined by high-resolution laser spectroscopy help us to understand the halo nucleus structure, and the results could be used to test different nuclear models. The halo nucleus is a weak bounding nucleus with a certain dilute nuclear matter distributed around the tightly bound core. Lithium isotope ¹¹Li is a well-known two-neutron halo nucleus, and it is described as a ⁹Li-like core with the two weakly-bound neutrons around it, like a “halo”. Some other examples of the halo nuclei are as follows: one-proton halo nuclei ⁸B and ¹³N, one-neutron halo nuclei ¹¹Be, ¹⁷C, and ¹⁹C, two-neutron halo nuclei ⁶He and ¹⁷B, four-neutron halo ⁸He, etc.

Due to the development in the laser spectroscopy during last decades it has become possible to study the nuclear properties including the spins, hyperfine structures, and charge radii of the short-lived nuclei by measuring the isotope shifts.^[7,8] In general, the IS has two contributions: the mass shift (MS) and the field shift (FS). The MS and the FS, in which different nuclear information is encoded accordingly, could not be distinguished from each other in the total IS by the experimental measurements. In order to separate the FS from the total IS, a new method of combining the atomic theory calculations and the high-resolution laser spectroscopy measurements has been developed,^[9,10] and then different experiments of the IS measurements have been carried out with different isotope sequences, such as Li, Be, Li-like Nd isotopes, etc., including the short-lived nuclei. Many theoretical and experimental schemes for other few-electron systems have also been proposed and made progress.^[11–15] The IS measurements and calculations of these few-electron systems are not only significant for nuclear properties but also important for nuclear theories.^[15–17]

As far as the lithium isotopes are concerned, the D lines between 2s²S_1/2 and 2p²P_J (J = 1/2, 3/2) have been used for the precise experiment investigations by optical pumping and NMR detection to study the nuclear properties, such as the ISs and fine structure intervals between ⁶Li and ⁷Li,^[18] nuclear magnetic and quadrupole moments of ⁸Li, ⁹Li, and ¹¹Li,^[19–21] etc. Another experiment of IS measurements for lithium isotopes has been carried out by using the two-photon transition from 2s²S_1/2 to 3s²S_1/2 and the nuclear charge radii of the short-lived lithium isotopes have been obtained.^[22] In the present paper, we calculate the ISs of the stable and short-lived lithium isotopes for the 2s²S_1/2 to 2p²P_J (J = 1/2, 3/2) atomic transition by using the multi-configuration Dirac–Hartree–Fock (MCDHF) method. We use a new version of a general relativistic atomic structure package named GRASP2K^[23] and a modified relativistic isotope shift code package^[24,25] to perform our calculations. Since lithium is a typical three-electron system, the IS calculation could be used to test the atomic computation theory. Furthermore, there are several short-lived isotopes including the brilliant halo nucleus ¹¹Li, our calculation will provide useful references for further checking the consistency among nuclear structural models.

We now outline the general isotope shift calculation theory by following Refs. [26]–[28]. The optical frequency of an atomic spectral line k linking the atomic energy levels l and u, with the level energy E_u > E_l, can be expressed as follows:

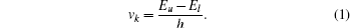
The total IS between two different isotopes A and A′ is made up of MS and FS, and is given by

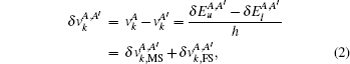
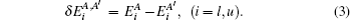
The MS is usually divided into two parts: the normal mass shift (NMS) and the special mass shift (SMS). The NMS is given by a simple replacement of the electron mass with the reduced mass of the system, and the SMS is caused by the effect of the electron correlations on the nuclear motion.

The FS in the atomic IS is produced by the difference in nuclear charge density distribution between the isotope nuclei. For the transition k between the atomic levels l and u with E_u > E_l, the FS of the different isotopes A and A′ can be written as

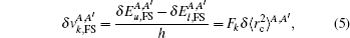
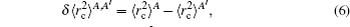
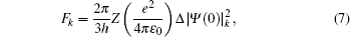
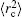
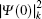
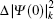
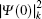
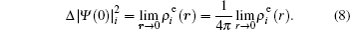
The total isotope shift could then be obtained by simply adding together the MS (including NMS and SMS) and FS contributions

The wave functions of the atomic levels in the MCDHF method are given by a linear combination of configuration state functions with the mixing coefficients, and the mixing coefficients could be obtained by the iterative method. The relativistic configuration interaction (RCI) approach^[23,24] is used in our calculations with a set of fixed pre-optimized orbitals and a set of variable mixing coefficients. We treat the nuclear motion and volume effects by the first-order perturbation theory and take into account the relativistic configuration interaction wave functions serving as zero-order functions in our calculations. The zero-order wave function is considered in terms of a configuration state expansion as follows:

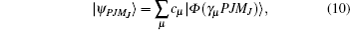
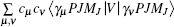
The nuclear data of the lithium isotopes, including the atomic mass, nuclear magnetic moment, and the changes in RMS nuclear radii are listed in Table 1. We give priority to the latest experimental results while collecting the nuclear data. Combining the available nuclear data with the results from the theoretical methods mentioned above, the ISs for the lithium isotopes including the MS and FS could then be obtained.

Table 1.

Table 1.

Table 1. Values of nuclear spin I, half-time τ, atomic mass M, nuclear magnetic moment μI, nuclear quadrupole moment Q, RMS nuclear charge radii r̄c, and the differences of the RMS nuclear charge radii of the lithium isotopes. . τ [29]/ms M [30]/u I [31] μI (μN)[31] Q [31]/e·fm2 r̄c [32]/fm 6Li Stable 6.01512280(2) 1 0.8220473(6) −0.083(8) 2.517(30) 0.622(38) 7Li Stable 7.01600455(9) 3/2 3.2564625(4) −4.06(8) 2.39(3) 0 8Li 838(6) 8.02248736(10) 2 1.65340(2) 3.27(6) 2.299(32) −0.427(39) 9Li 178.3(4) 9.026790(2) 3/2 3.4391(6) −2.74(1) 2.217(35) −0.796(54) 11Li 8.59(14) 11.043716(6) 3/2 3.668(3) −3.1(5) 2.467(37) 0.374(54)

Table 1. Values of nuclear spin I, half-time τ, atomic mass M, nuclear magnetic moment μI, nuclear quadrupole moment Q, RMS nuclear charge radii r̄c, and the differences of the RMS nuclear charge radii of the lithium isotopes. .

The electron correlation effects are also evaluated by the MCDHF method and the computation package. For lithium atom with two inner electrons and one valence electron, the core–valance correlation and the inner–valance correlation are involved. We use the double excitation mode to carry out our calculations and the active configurations are expanded from occupied orbitals to some active sets layer by layer. In this work, the largest principal quantum number n = 10 and the maximum orbital quantum number l = g. The relativistic mass shift parameters and field shift factors for the 2s²S_1/2 and 2p²P_J (J = 1/2, 3/2) transitions of lithium are presented in Table 2. The parameter ΔK′ is defined as ΔK′ = ΔK/h in unit of GHz·amu and the individual contributions of the relativistic normal mass shifts and specific mass shifts are presented as well. The unit of the F factors is MHz/fm².

Table 2.

Table 2.

Table 2. Values of relativistic mass shift parameter ΔK′ with the unit of GHz·amu and the field shift parameter F with the unit of MHz/fm2 for the 2s2S1/2 and 2p2PJ (J = 1/2, 3/2) transitions of lithium. The parameter ΔK′ is defined as ΔK′ = ΔK/h. . 2s–2p1/2 2s–2p3/2 This work Ref. [22] This work Ref. [22] −247.297 −247.285 −196.612 −196.639 −443.909 −444.086* −443.924 −444.103* F −2.447 −2.457 −2.447 −2.457 * Cited from Ref. [22] with the mass shifting between 6Li and 7Li.

Table 2. Values of relativistic mass shift parameter ΔK′ with the unit of GHz·amu and the field shift parameter F with the unit of MHz/fm2 for the 2s2S1/2 and 2p2PJ (J = 1/2, 3/2) transitions of lithium. The parameter ΔK′ is defined as ΔK′ = ΔK/h. .

The isotope shifts including the NMS, SMS, and FS of the lithium isotopes for the transitions between 2s²S_1/2 and 2p²P_J (J = 1/2, 3/2) are shown in Table 3 with the unit of MHz. The reference isotope is ⁶Li and the ISs in Table 2 are defined as δν^A,6 = ν^A − ν⁶ (A = 7, 8, 9, and 11), respectively.

Table 3.

Table 3.

Table 3. Lithium isotope shifts including the NMS, SMS, and FS for the 2s2S1/2 to 2p2PJ (J = 1/2, 3/2) transitions in the unit of MHz. The reference isotope is 6Li. . 2s–2p1/2 2s–2p3/2 7Li 8Li 9Li 11Li 7Li 8Li 9Li 11Li NMS 5867.97 10291.98 13722.89 18727.89 5867.68 10291.49 13722.23 18726.99 SMS 4665.29 8182.58 10910.30 14889.49 4665.93 8183.71 10911.81 14891.55 MS 10533.26 18474.56 24633.19 33617.38 10533.62 18475.20 24634.04 33618.54 FS 1.53 2.58 3.48 0.61 1.53 2.58 3.49 0.61 IS 10534.78 18477.14 24636.67 33617.99 10535.15 18477.77 24637.52 33619.15

Table 3. Lithium isotope shifts including the NMS, SMS, and FS for the 2s2S1/2 to 2p2PJ (J = 1/2, 3/2) transitions in the unit of MHz. The reference isotope is 6Li. .

We now come to compare our results with previous calculations and experimental results (see Table 4). There have been many theoretical and experimental results for D lines ISs between ⁶Li and ⁷Li, but only few theoretical values for other short-lived isotopes up to now. The results of the IS measurements for D lines of ⁶Li and ⁷Li are mainly in the vicinity of 10534 MHz, which are in good agreement with our calculations. The IS calculations in Refs. [9] and [22] are performed by the QED correction treatments, each with an additional uncertainty of ±3 MHz due to the mass-independent QED terms, which is the same for both isotopes and can be cancelled exactly. Owing to this cancellation, the ISs can be calculated to a sufficiently high accuracy. The results cited from Ref. [22], which should be added by a second uncertainty of ±0.61 MHz due to the nuclear size correction, are as follows: the mass shifts are 10532.111(6) MHz and 10532.506⁽⁶⁾ MHz for the 2s_1/2–2p_1/2 and 2s_1/2–2p_3/2 transitions, respectively, and the field shifts are both 1.94⁽⁶¹⁾ MHz. The field shifts of our results in Table 3 for the ⁷Li–⁶Li cases are all 1.53 MHz, which are different from those in Refs. [9] and [22]. The difference could be accounted for by different assumed values for the nuclear radii, and the charge radii of ⁶Li are 2.55 fm in Refs. [9] and [22], and 2.517 fm in our calculations. There is a large uncertainty of 300 MHz of the theoretical calculations in Ref. [33], which is carried out by the configuration interaction (CI) and many-body perturbation theory (MBPT). The calculations in Ref. [34] are performed by the non-relativistic multi-configuration Hartree-Fock method and the result of IS with 10528.7 MHz for the 2s–2p_1/2 transition is close to our result.

Table 4.

Table 4.

Table 4. Comparisons between previous theoretical and experimental values for the 2s2S1/2–2p2PJ (J = 1/2, 3/2) transitions (in MHz). . 2s–2p1/2 2s–2p3/2 7Li 8Li 9Li 11Li 7Li 8Li 9Li 11Li Theory This work 10534.78 18477.14 24636.67 33617.99 10535.15 18477.77 24637.52 33619.15 Ref. [9] 10534.13(7) 18472.86(12) 24631.11(16) 33615.19(24) 10534.52(7) 18473.55(12) 24632.03(16) 33616.45(24) Ref. [22] 10534.051(6) 10534.520(6) Ref. [33] 10608(300) 10607(300) Ref. [34] 10528.7 Experiment Ref. [18] 10534.215(32) 10533.352(68) Ref. [35] 10534.039(70) 10534.194(104) Ref. [36] 10533.160(68) Ref. [37] 10534.3(3) 10539.9(12)

Table 4. Comparisons between previous theoretical and experimental values for the 2s2S1/2–2p2PJ (J = 1/2, 3/2) transitions (in MHz). .

The uncertainties of our results mainly come from two parts: one part is because of the uncertainties of the atomic data listed in Table 1, such as the atomic mass and the difference between RMS nuclear charge radii used in our calculations; another part is attributed to the fact that the atomic orbitals could not be included overall, in our calculations the largest principal quantum number is n = 10. The first part gives the uncertainty contribution of about 1 MHz and the second part will lead to several MHz variations. The total uncertainty in our results are evaluated finally to be about ±5 MHz and the corresponding relative error is less than 0.05%. For lithium isotopes, the ±5 MHz derivation is too large to separate the FS contributions from the total IS. In fact, as shown in Table 2, the differences in IS parameters between our calculations and the results in Ref. [22] is very tiny, which confirms that our calculations could be used for the consistent checks of different theoretical calculation methods. We should note that the mass shift decreases rapidly approximately with increasing mass number A as A⁻² and the field shift increases in proportion to Z²A^−1/3, where Z is the nuclear charge number. Therefore, the MCDHF method and RCI approach used here could be referred to the IS calculations of other heavier Li-like ions and the IS parameters, and the individual contributions of NMS, SMS and FS could be obtained accordingly.

In this work, we present the IS calculations for the D lines of the stable and short-lived lithium isotopes using the MCDHF method and RCI approach. The new version of atomic structure package GRASP2K and a modified relativistic isotope shift code package are used to carry out our calculations. The IS parameters and the individual contributions of NMS, SMS, and FS are calculated respectively. Our results are in good agreement with previous theoretical calculations and experimental measurements. The detailed discussion and the comparison between our results and previous results are conducted. The methods and code packages used herein could be applied to the IS calculations of other heavier Li-like ions or few-electron systems.