† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 41674088, 11574254, 11272296, and 11547311), the National Basic Research Program of China (Grant No. 2011CB808201), the Fundamental Research Fund for the Central Universities, China (Grant Nos. 2682014ZT30 and 2682014ZT31), and the Fund of the State Key Laboratory of Solidification Processing in Northwestern Polytechnical University, China (Grant No. SKLSP201511).
First-principle simulations have been applied to investigate the effect of copper (Cu) or aluminum (Al) content on the ductility of Al3Ti, AlTi, AlCu, and AlTiCu2 alloys. The mechanical stable and elastic properties of Al-based intermetallic compounds are researched by density functional theory with the generalized gradient approximation (DFT-GGA). The calculated lattice constants are in conformity with the previous experimental and theoretical data. The deduced elastic constants show that the investigated Al3Ti, AlTi, AlCu, and AlTiCu2 structures are mechanically stable. Shear modulus, Young’s modulus, Poisson’s ratio, and the ratio B/G have also been figured out by using reckoned elastic constants. A further analysis of Young’s modulus and Poisson’s ratio reveals that the third added element copper content has significant effects on the Al–Ti-based ICs ductile character.
Since the early part of the last century, intermetallic compounds (ICs) have attracted considerable attention due to their unique physical properties and wide prospects in industries and electronics,[1–5] such as: mechanical help, welding alloys, alloy materials of sacrificial anodes, heat-resistant alloys, electricity, preferred material of mechanical heart valve and components.[6,7] As one potential industrial applied material, aluminum–titanium alloys possess elevated-temperature strength, low density, high melting points and strength.[8] They have been the desirable candidate-materials for structural applications, electricity and electronic devices.[9] Unfortunately, Al–Ti alloys are hard to be applied directly in practice industry for Al–Ti ICs brittleness and bad plastic deformation.[10–15] In order to improve the ductile properties of Al–Ti ICs, we put out a hypothesis added copper element into Al–Ti alloys that could improve Al–Ti ICs ductile and mechanical properties.
As we all know, Cu-based ICs have showcased for a new talent in biomechanical applications, aerospace and connectors with their perfect mechanical and physical ductile properties.[16–19] Especially, their brittleness is mainly due to the strong directional metallic-covalent bonds, which is based on the bonding mechanism by Osman et al.[20] In view of the present situation, an original plan is revised that the added element could decrease the content of Al percent, and increase the ductile character of Al–Ti alloy with the content of Cu. Of course, there are some corroborated experiments and theory evidences to support this initial hypothesis.[21] Other scientists have found that the mechanical characters can be improved due to the phase transition, especially, Al3Ti structure.[22,23] Hence, we can add the third element copper into Al–Ti alloys to make Al–Ti ICs become an eminent and ductile material. In this way, adding the third element copper into the binary systems would be an elegant way of gaining ideal Al–Ti-based alloys. At the same time, Zhang et al.[21] has proved that Cu could increase the strength of the in situ composites substantially due to the introduction of more strengthening modes and more reinforcing particles. However, there is no related evidence that the added Cu can improve Al–Ti–X ductile character.
To gain more knowledge about Al–Ti–X ductile character, this study mainly focuses on Al3Ti, AlTi, AlCu, and AlTiCu2 structural and mechanical properties. In this paper, we present a detailed study of these mechanical and physical properties of AlTiCu2 by using the first-principles plane-wave pseudopotential method.
All calculated works were done by using the Cambridge Serial Total Energy Package Code (CASTEP) based on the density functional theory (DFT) scheme and an implementation of the ultra-soft pseudo-potential plane-wave (UPPW) methods.[17–20] Exchange and correlation theory was employed with the generalized gradient approximation or called GGA.[21,22] 3s23p of Al, 3d24s2 of Ti, and 3d104s2 of Cu were considered as valence electrons. In this paper, the cutoff energy of plane-wave was 450 eV. The other parameters were set as a total energy convergence of 5.0 × 10−6 eV/atom, a maximum force of 0.01 eV/Å, a maximum stress of 0.02 GPa, and a maximum displacement of 5.0 × 10−4 Å. Al3Ti, AlTi, AlCu, and AlTiCu2 parameters were reckoned and probed by the popular Brodyden–Fletcher–Goldfarb–Shanno (BFGS) means.[23–26] For the different kinds of structures calculated, the Brillouin zone integrations were sampled with various (Γ point centered) k points which are generated by the scheme of Monkhorst–Pack grids (shown in Table
| Table 1. Lattice parameters (a and c), space groups, and k-point mesh. . |
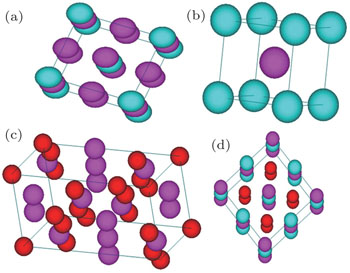
The different space groups of Al3Ti, AlTi, AlCu, AlTiCu2 are studied and shown in Fig.
Clearly, the calculated lattice constants are in good agreement with the previous experiments data. The deviations are less than 1%. Through these reliable calculated results, the structural data indicate that this method is a credible and applied method in this research work. Thereby, the GGA-PBE method and optimized lattice constant could be suited for subsequent calculations, including Al3Ti, AlTi, AlCu, AlTiCu2 mechanical properties, even other physical characters.
Elastic constants of different Laves phases are important for the actual application of our life. Simultaneously, elastic properties of solids are very closely related to various fundamental physical properties, such as bulk modulus (B), shear modulus (G), Young’s modulus (E), Poisson’s ratio (v), melting point, Debye temperature, and thermal expansion coefficient. Maybe, this is the reason why elastic constants Cij play a significant role in ICs materials. The gross energy and a small strained equation is given by[32]
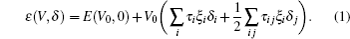

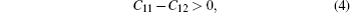
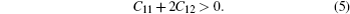


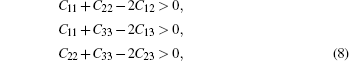
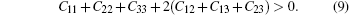





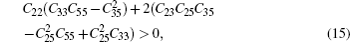
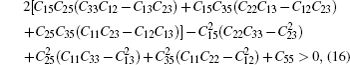
Elastic constants are shown in Table
| Table 2. Calculated elastic constants. . |
As a systematical response to Al3Ti, AlTi, AlCu, AlTiCu2 alloy material mechanical properties, bulk modulus B, shear modulus G, Young’s modulus E, and Poisson’s ratio σ are also summarized in Table
| Table 3. Calculated bulk modulus B, shear modulus G, and Young’s modulus E of Cu–Ti ICs. . |
For the cubic structure, the shear modulus G and bulk modulus B are given approximately as[33,35]
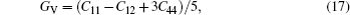


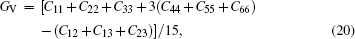
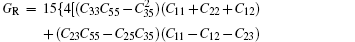
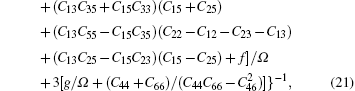
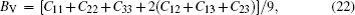
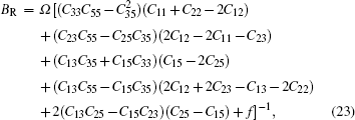
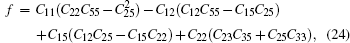
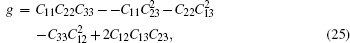
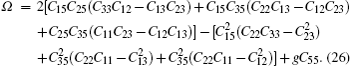
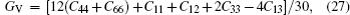
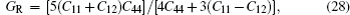
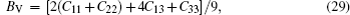
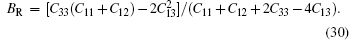
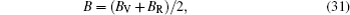
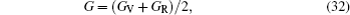
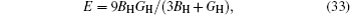
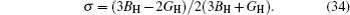
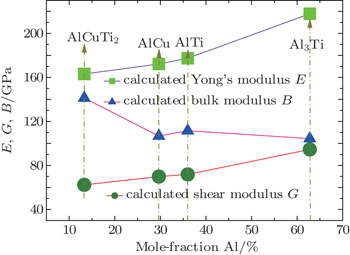
Bulk modulus B, shear modulus G, and Young’s modulus E for Al3Ti, AlTi, AlCu, AlTiCu2 are calculated according to Eqs. (
Young’s modulus is always a pretty character about the stiffness of ICs materials. The larger Young’s modulus is, the harder the material is. In Fig.
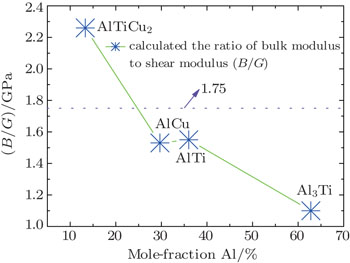 | Fig. 3. Theoretically calculated the ratio of bulk modulus to shear modulus (B/G) of Al3Ti, AlCu, AlTi, AlTiCu2as a function of Al content. |
In this part, plasticized properties of Al3Ti, AlCu, AlTi, AlTiCu2 are characterized by the ratio of bulk modulus to shear modulus (B/G), which can describe the plastic characteristic of materials.[40,45] A large B/G value means that the material tends to perform with a ductile property, while, a small value means it has a tendency to a brittleness property. The standardized value distinguishing ductile and brittle materials has been evaluated to be 1.75.[40] The B/G ratio is shown in Table
Poisson’s ratio σ is distinguished by the level of different bonds in this work. For Ionic crystal, σ is usually looked at as 0.25. While, for the value of covalent materials, σ is not equal ionic crystals (σ = 0.1).[45] The calculated σ is given in Table
In this paper, we have systemically investigated the alloying stability, the mechanical and thermodynamic properties of Al3Ti, AlCu, AlTi, and AlTiCu2 by the first-principles method. The conclusions are listed in the following points.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 |