Cite this Article
Cao Ya, Gao Fei. Cryptanalysis of quantum broadcast communication and authentication protocol with a one-time pad. Chinese Physics B, 2016, 25(11): 110305  
Permissions
Cryptanalysis of quantum broadcast communication and authentication protocol with a one-time pad
Cao Ya1, 2, Gao Fei1, †,
State Key Laboratory of Networking and Switching Technology, Beijing University of Posts and Telecommunications, Beijing 100876, China
State Key Laboratory of Cryptology, Beijing 100878, China

 

† Corresponding author. E-mail: caoshinee@126.com

Project supported by the National Natural Science Foundation of China (Grant Nos. 61272057 and 61170270).

Abstract
Abstract

Chang et al. [Chin. Phys. B 23 010305 (2014)] have proposed a quantum broadcast communication and authentication protocol. However, we find that an intercept-resend attack can be preformed successfully by a potential eavesdropper, who will be able to destroy the authentication function. Afterwards, he or she can acquire the secret transmitted message or even modify it while escaping detection, by implementing an efficient man-in-the-middle attack. Furthermore, we show a simple scheme to defend this attack, that is, applying non-reusable identity strings.

PACS: 03.67.Dd;03.67.Hk;03.67.–a;03.65.Ud
Keyword:quantum broadcast communication;quantum secure direct communication;Greenberger–Horne–Zeilinger (GHZ) state;authentication
1. Introduction

Cryptography aims at sharing secret messages between users, while revealing nothing to eavesdroppers. In classical cryptography, most schemes are conditionally secure under the assumption of computational complexity, except for the one-time pad (OTP) crypto-system. In OTP, an unconditional secure string is used to encrypt messages to be transmitted in a public way. The major difficulty of the OTP crypto-system comes from how to securely distribute key bits. Quantum key distribution (QKD) is such a mechanism to transfer an unconditional secure string. Since the first QKD protocol was proposed by Bennett and Brassard in 1984,[1] QKD has attracted a great deal of attention because of its attractive property of being unconditionally secure, and a lot of QKD protocols have been presented.[2–9] Besides QKD, a variety of quantum cryptography has been proposed, such as quantum secret sharing (QSS),[10–13] quantum signature (QS),[14–17] and quantum private queries (QPQ).[18–24] In the last few years, QPQ has become a subject of intense focus. It solves the most concerned problem of privacy of both database and users, which still needs to be further studied.

Recently, quantum secure direct communication (QSDC) appeared as a novel branch of QKD.[25–40] Different from QKD, QSDC is to realize the task of transmitting messages directly, without pre-shared secret keys. The first QSDC was presented by Beige et al. with a single photon in 2001.[25] In 2002, Boström and Felbinger put forward a ping-pong scheme with Einstein–Podolsky–Rosen (EPR) pairs.[26] However, the ping–pong scheme is proved to be quasisecure when using a perfect quantum channel.[27] Later, in order to improve the security, Deng et al. presented a two-step QSDC scheme.[28] In their paper, a sequence of ordered EPR pairs is prepared and then divided into two subsequences, where one serves as the checking string and the other as the message-encoding string. In 2004, Deng and Long presented a QSDC scheme with a one-time pad crypto-system which is more practical.[29] Thereafter, the investigation into multiparty QSDC schemes has naturally been considered.[41]

Quantum broadcast communication (QBC)[41–43] is one kind of multiparty QSDC scheme. QBC is a scheme which attempts to transmit secret messages from the sender Alice to a dynamically changing group of users (Bob, Charlie, ...) through broadcasting channels. QBC ensures only authorized users obtain subscribed information and others can learn nothing. In 2007, Wang et al. proposed three QBC schemes, where identity authentication is realized by utilizing hash function and local unitary operations.[42] Later in 2010, Yang et al. improved the scheme of Wang et al. in efficiency, and also used the hash function to authenticate identity.[43] It is known that design is an important work in cryptography. As pointed out by Lo and Ko, breaking cryptographic systems was as important as building them.[44] Cryptanalysis is also important for quantum cryptography.[45–50] It helps estimate the security of a protocol, find potential loopholes in it, and improve it to level up the security.

More recently, Chang et al. proposed a quantum broadcast communication and authentication (QBCA) protocol,[51] based on the Greenberger–Horne–Zeilinger (GHZ) state and a one-time pad crypto-system. This protocol is easier to be implemented than that referred to by Wang et al.[42] and Yang et al.[43] The reason is that Chang et al.’s protocol gives up hash functions and local unitary operations for eavesdropping detection and authentication, but applies a reusable pre-shared binary string serving as an identity string, and the classical XOR operation. However, the security requirements may not be satisfied as mentioned in Chang et al.’s protocol.

In this paper, we study and analyze the security of Chang et al.’s QBCA protocol. We implement a devised intercept-resend attack, which introduces no error. By applying this attack, a potential eavesdropper Eve can successfully deduce the identity strings, which are the symbols of authorized users. With these identity strings, Eve has the capacity to implement an efficient man-in-the-middle attack.[56] That is to say, Eve can impersonate an authorized user to communicate with the sender and obtain the transmitted message, or the sender to transfer the transmitted message or even a modified one (e.g., a useless message) to authorized users, while not being detected. To avoid this loophole, we also put forward a possible manner to help suffer the intercept-resend attack.

The rest of this paper is arranged as follows. In Section 2, we review Chang et al.’s QBCA protocol in detail. In Section 3, we introduce a devised intercept-resend attack for Chang et al.’s protocol and give an improved scheme to avoid the weakness and an analysis to prove it to be effective. Finally, we conclude this paper.

2. Review of Chang et al.’s protocol

In this section, we review Chang et al.’s protocol. Before the scheme starts, there are some assumptions. Suppose Alice is the sender, and Bob and Charlie are the two legitimate receivers. The secret message to be transmitted is a classical string. Alice pre-shares an N-bit identity string IDB and IDC with Bob and Charlie, respectively. The details of Chang et al.’s scheme are described below.

Step 1 Alice generates three sequences of quantum states, one serving as the information carrier, and the other two as decoy states. Firstly, she prepares a sequence of ordered N triplet GHZ states in the form . She then divides the N GHZ states into three ordered particle sequences S1, S2 and S3, respectively, where the subscript indicates which sequence each particle of every state belongs to. After that, she prepares N-qubit sequences SIDB and SIDC according to IDB and IDC, respectively. Taking SIDB as an example, if the i-th bit of IDB (denoted as IDBi) is 0, is randomly encrypted by qubit |0〉 or |1〉; otherwise, is randomly encrypted in state |+〉 or |−〉. SIDC is prepared in the same way.

Step 2 Alice inserts SIDB and SIDC into S2 and S3, constructing new sequences and , respectively. Concretely, if IDBi = 0, Alice inserts behind ; otherwise, she inserts it before . She constructs with the same method. Then Alice transmits and to Bob and Charlie, respectively.

Step 3 Bob and Charlie distinguish SIDB and SIDC from and with the knowledge of IDB and IDC, respectively. Then they both measure SIDB and SIDC with corresponding bases of SIDB and SIDC.

Step 4 Alice requires Bob and Charlie to declare the state of each photon in SIDB and SIDC, but not including the basis information. One possible way for Bob and Charlie is to publish bit 0 for the result |0〉 or |+〉, and 1 for |1〉 or |−〉. Then Alice authenticates them by comparing the announced information with the initial states of SIDB and SIDC. If the error rates are low enough, Alice confirms Bob and Charlie are legitimate users and believes there are no eavesdroppers. Then they proceed to the next step. Otherwise, Alice stops this communication.

Step 5 Bob and Charlie use the Z basis to measure every photon in S2 and S3, forming ordered classical sequences CS2 and CS3, respectively. Bob and Charlie both announce which photons they do not receive in S2 and S3 in order. For lost photons, Alice discards corresponding photons in S1, so do Bob and Charlie. Then Alice measures the remaining photons in S1 with Z basis forming an ordered classical sequence CS1. Suppose CS1 is an N1-bit string. Alice takes the first N1 bit from secret message M as M1, and encrypts it with CS1 using the XOR operation bit by bit to obtain encrypted message C. Then Alice publishes C.

Step 6 Bob and Charlie decrypt C with CS2 and CS3, respectively, using XOR operation bit by bit, then obtain secret message M1 and store it. Till now, Alice, Bob, and Charlie complete one communication.

3. Analysis and improvement
3.1. Security analysis of Chang et al.’s QBCA protocol

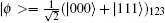
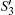
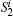
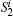
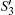
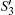
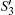
In Chang et al.’s QBCA protocol, the authors have proved the security based on the fact that the true random number CS1 used as a one-time pad is unknown to anyone else except Alice and Bob. Suppose an eavesdropper Eve, who does not know the number CS1, tries to obtain the transferred message, she will fail since the OTP is a secure system. However, is it true that Eve really cannot get the number CS1? To answer the question, we should first track the security foundation of the number CS1. CS1 is formed by measuring sequence S1 with the Z basis in order. A legal user Bob can deduce CS1 from S2. The security of S2 comes from the secure positions of the bits in S2 or SIDB, and identity string SIDB determines the positions. However, in Chang et al.’s QBCA protocol, Bob’s identity SIDB will be totally leaked out to Eve. The chance is given by that the identity string is reusable. Afterwards, we will prove it in detail.

We first introduce an intercept-resend attack to Chang et al.’s protocol to invalidate the authentication function and then implement a successful man-in-the-middle attack to obtain the transmitted message or even replace it with a modified one. It is obvious that, in Chang et al.’s protocol, the authorized users Bob and Charlie act in the same character to the sender Alice, and behave the same in the protocol. Without loss of generality, we take Bob as an example to analyze Chang et al.’s protocol.

Reviewing Chang et al.’s QBCA protocol, we find that the test for the authentication is also a test for potential eavesdroppers. Both processes functioning wells are due to the fact that just Alice and Bob know the pre-shared identity string. Without the identity IDB, an eavesdropper Eve cannot successfully cheat Alice to obtain the secret message. Since she does not know IDB, she cannot provide the proper information in Step 4, so Alice will calculate a high error rate and then detect Eve. However, in Chang et al.’s protocol, the identity string will be totally revealed. This is because of the statement that the identity string is reusable. By exploiting this little defect, we present an effective attack on Chang et al.’s protocol.

Eve attacks Chang et al.’s protocol using the following steps:

(A1) Eve enters the communication process. She impersonates one participant to contact with the other one, in order to excite the communication.

(A2) Once the communication starts, Eve intercepts every photon from Alice. Then she makes different movements to these photons, according to their positions in the sequence . If the photon is the 2i-th qubit of , Eve measures it with the Z basis and resends it to Bob; otherwise, the photon is the (2i + 1)-th qubit, and she just lets it go towards Bob. Here, i ranges from 1 to N.

(A3) Eve reveals the complete identity string IDB. When Chang et al.’s protocol proceeds to Step 4: the authentication and eavesdropping detection, Eve compares her measurement results with Bob’s announcement in order. Repeating this action for enough communications, she is able to obtain IDB, while not being detected by Alice.

Looking at Step 4 again, we find that, in , the secret qubit and decoy qubit always appear in pairs. That is, one of the (2i − 1)-th and 2i-th qubits in must belong to S2 and the other belongs to SIDB. Thus, every photon in the even position of is either a secret qubit or a decoy state corresponding to IDBi = 0. Another important point in Chang et al.’s authentication process lies in that Bob is asked to measure SIDB with the Z basis when IDBi = 0, as described in Step 4. However, secret photons should also be measured in the Z basis referring to Step 5. These two points ensure that Eve’s measurement does not disturb the process where Alice authenticates Bob.

Recalling Chang et al.’s protocol, they claimed that the legitimate receiver’s identity is a reusable classical string. That is, no matter how many times the protocol runs, Bob always use the same binary string IDB for authentication. Therefore, Eve can compare his results in many communications with Bob’s publication. As discussed above, for every even photon in , it might be a secret photon, then Eve’s measurement result will be equal to what Bob announces with probability 1/2; otherwise, it is a decoy photon whose corresponding bit in IDB is 0, then Eve’s result is always the same as Bob’s announcement. In ideal circumstances, as long as Eve finds there is one time that his measurement result is unequal to Bob’s announcement for the corresponding qubit in SIDB, he can confirm that the i-th identity bit IDBi is 1; if Eve’s measurement result is always equal to Bob’s corresponding announcement many times, he can believe IDBi is 0. In the later case, there are two situations for Eve and Bob to have equal results. However, the probability for the case that IDBi = 1 and induces the same results for n-times communications is (1/2)n, which will be smaller than 10−5 if n = 17. Hence, if there are enough times when the same results appear, Eve can confirm that IDBi is 0.

(A4) Finally, Eve obtains or modifies the secret message by implementing a man-in-the-middle attack.

After the step above, Eve holds the complete identity. When another communication happens, Eve launches it and two protocols are performed in parallel: one is between Alice and Eve, the other is between Eve and Bob. In the former one, Eve poses as a legitimate user. She just executes the protocol normally and the authentication will be passed since she holds the right identity of Bob. In the latter one, Eve acts as the sender. She prepares the necessary qubits to form a fake S2, called 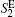, sends it to Bob, and passes the authentication. In this way, Eve achieves the man-in-the-middle attack on Chang et al.’s protocol. If Eve just wants to acquire the secret message without modifying it, an intercept-resend attack is enough. She first intercepts every photon transmitted by Alice. Then, Eve distinguishes which photon is from S2, and which one is from SIDB. If the photon comes from SIDB, she just lets it go. Otherwise, she measures it with the Z basis, and then sends it to Bob. Since Eve does nothing to the decoy states, the detection is not disturbed. So Alice’s test will be passed. On the other hand, CS2, which decrypts the secret message, is constructed by measuring S2 with the Z basis. So Eve’s measurement will then reveal the secret message M.

As a result, we successfully make our intercept-resend attack on Chang et al.’s protocol. With this attack, Eve acquires the secret identity string SIDB, while introducing no error. On the one hand, she can obtain the secret message which is transferred to authorized user Bob. On the other hand, she will not be detected by the sender Alice. Moreover, by implementing a man-in-the-middle attack, she can impersonate Alice and send Bob a fake message instead of the right one, but Bob will be unaware of it. As mentioned earlier, if we substitute Charlie for Bob in the above process, the analysis and results will be all the same. Furthermore, since Chang et al.’s protocol can be generalized to a multi-party one, our attack also works on the generalized one.

3.2. Improvement of Chang et al.’s protocol

Now we consider how to improve Chang et al.’s protocol. As we have emphasized, the reason why Chang et al.’s protocol is fragile lies in that the identity string is claimed to be reusable. This gives an eavesdropper Eve a chance to play the intercept-resend attack successfully and obtain the secret identities. To plug this loophole, the sender should not pre-share a reusable identity with the user. We modify the protocol as follows.

(R1) Before the protocol starts, we made a substituted supposition that Alice pre-shares an identity store IDB = {IDB1, IDB2,...}, with Bob and IDC = {IDC1, IDC2,…} with Charlie. Here, each element from IDB and IDC is a string encoded Bob’s and Charlie’s identity, respectively. They fix a rule to decide the order where these identities are to be used.

The simplest rule is that they agreed to use the identity in order. That is to say, in round 1, Alice uses IDB1 to run the protocol with Bob, and IDC1 with Charlie, and Bob and Charlie choose IDB1 and IDC1, respectively; in round 2, Alice picks IDB2 and IDC2. Meanwhile, Bob uses IDB2, and Charlie uses IDC2; etc. They also can make the rule more complex by applying a hash function. A possible way is that Alice, Bob, and Charlie share the same hash function H. They count the run number x, and pick the H(x)-th identity, respectively.

(R2) When the protocol begins, Alice picks out identities IDBi and IDCi from the identity stores according to the agreed rule, and Bob and Charlie choose the corresponding identity, respectively.

The following steps in Chang et al.’s protocol are not necessary to be amended. With our strategy, the modified version is able to suffer from the presented intercept-resend attack. In our scheme, we abandon the reusable identity, but utilize a non-reusable identity store. As we have analyzed before, an eavesdropper Eve cannot deduce one bit of the identity if she gets the same result to what Bob announced, for the reason that she is not sure whether this bit corresponds to a qubit from SIDB or S2. However, this bit is certainly from SIDB corresponding to an identity bit 1, when Eve finds her result is different from that of Bob. On the one hand, for one communication, it is obvious that this attack cannot reveal the complete identity. On the other hand, one may consider whether he can do more with this imcomplete identity or not. However, as pointed out in the Ref. [34], it is not sufficient for him to perform a man-in-the-middle attack or generate fake photons. Furthermore, we update the identity in each communication, so the revealed identity information cannot provide efficient information for the next communication. Thus comparing results from multi-communications is also not an available way for Eve to attack this modified version. Therefore, the modified protocol with non-reusable identity is successful.

To illustrate our analysis in more detail, we make a comparison between the reusable version and the modified one about the information leakage by giving an example. Considering Bob, the simplest case is that there are only two identity strings in IDB, IDB1 and IDB2. However, the protocol with a reusable identity just has IDB1. Suppose each identity concludes one bit, and let IDB1 = 1 and IDB2 = 0. As shown in Table 1, the probability for the modified version to leak a bit is 1/4; however, this probability is 1/2 in the reusable one.

Table 1.

Comparison between reusable and non-reusable version. ID denotes the corresponding bit of IDB1 and IDB2. represents the possible states of after Eve’s and Bob’s measurement.

.
4. Conclusion

In this paper, we have pointed out that there is a loophole in Chang et al.’s QBCA protocol, where an eavesdropper can impersonate any legitimate participants in communication and not be detected. Eve first obtains the secret identity strings of legitimate receivers through an intercept-resend attack without being detected. Then she is able to obtain or modify the transmitted message by impersonating both the sender and legitimate receivers, while not disturbing the protocol. Besides, we present a simple strategy to avoid this loophole by sharing secret identity stores between the sender and authorized users. The security analysis shows the improved scheme is capable of surviving this intercept-resend attack. This makes the improved one more secure.

Reference
1BennettC HBrassardG1984Pro. IEEE Int. Conf. on Computers, Systems and Signal ProcessingNew YorkIEEE175
2SunYWenQ Y 2010 Phys. Rev. 82 052318
3WangC ZGuoHRenJ GCaoYPengC ZLiuW Y 2014 Science China Physics, Mechanics and Astronomy 57 1233
4LuX MZhangL JWangY GChenWHuangD JLiDWangSHeD YYinZ QZhouYHuiCHanZ F 2015 Science China Physics, Mechanics and Astronomy 58 120301
5LiYBaoW SLiH WZhouCWY 2015 Chin. Phys. 24 110307
6WangLZhaoS MGongL YChengW W 2015 Chin. Phys. 24 120307
7LiYBaoW SLiH WZhouCWY2015Chin. Phys. B2510305
8AnX BYinZ QHanZ F 2015 Acta Phys. Sin. 64 140303 (in Chinese)
9SunYZhaoS HDongC 2015 Acta Phys. Sin. 64 140304 (in Chinese)
10DengF GLiX HZhouH YZhangZ J 2005 Phys. Rev. 72 044302 (in Chinese)
11QinS JGaoFWenQ YZhuF C 2006 Phys. Lett. 357 101 (in Chinese)
12YangY GChaiH PWangYTengY WWenQ Y 2011 Science China Physics, Mechanics and Astronomy 54 1619
13SunYGaoFYuanZLiY BWenQ Y 2012 Quantum Information Processing 11 1741
14ChoiJ WChangK YHongD 2011 Phys. Rev. 84 062330
15ZhangK JSongT TZuoH JZhangW W 2013 Physica Scripta 87 045012
16YuC HGuoG DLinS 2014 Science China Physics, Mechanics and Astronomy 57 2079
17WangT YCaiX QRenY LZhangR L 2015 Sci. Rep. 5 9231
18GaoFLiuBWenQ YChenH 2012 Opt. Commun. 20 17411
19ZhangJ LGuoF ZGaoFLiuBWenQ Y 2013 Phys. Rev. 88 022334
20WeiC YGaoFWenQ YWangT Y 2014 Sci. Rep. 4 7537
21YangY GSunS JXuPTianJ 2014 Quantum Information Processing 13 805
22GaoFLiuBHuangWWenQ Y 2015 IEEE Journal of Selected Topics in Quantum Electronics 21 98
23LiuBGaoFHuangWWenQ Y 2015 Science China Physics, Mechanics and Astronomy 58 100301
24WeiC YWangT YGaoF 2016 Phys. Rev. 93 042318
25BeigeAEnglertB GKurtsieferCWeinfurterH 2002 Journal of Physics A: Mathematical and General 35 L407
26BoströmKFelbingerT 2002 Phys. Rev. Lett. 89 187902
27WójcikA 2003 Phys. Rev. Lett. 90 157901
28DengF GLongG LLiuX S 2003 Phys. Rev. 68 042317
29DengF GLongG L 2004 Phys. Rev. 69 052319
30ZhangZ JLiuJWangDShiS H 2007 Phys. Rev. 75 026301
31LinSWenQ YGaoFZhuF C 2008 Phys. Rev. 78 064304
32QinS JWenQ YMengL MZhuF C 2009 Science in China Series G: Physics, Mechanics and Astronomy 52 1208
33LiuDPeiC XQuanD XZhaoN 2010 Chin. Phys. Lett. 27 050306
34GaoFQinS JGuoF ZWenQ Y 2011 Chin. Phys. Lett. 28 020303
35HuangWWenQ YJiaH YQinS JGaoF 2012 Chin. Phys. 21 100308
36ChangYXuCZhangSYanL 2014 Chin. Sci. Bull. 59 2541
37ZouX FQiuD W 2014 Science China Physics, Mechanics and Astronomy 57 1696
38ZawadzkiP 2015 Quantum Information Processing 14 2589
39MaH YQinG QFanX KChuP C 2015 Acta Phys. Sin. 64 160306 (in Chinese)
40LiX H 2015 Acta Phys. Sin. 64 160307 (in Chinese)
41DengF GLongG LWangYXiaoL 2004 Chin. Phys. Lett. 21 2097
42WangJZhangQTangC J 2007 Chin. Phys. 16 1868
43YangY GWangY HWenQ Y 2010 Chin. Phys. 19 070304
44LoHKoT2005Quantum Information Processing541
45DengF GLiX HZhouH YZhangZ j 2005 Phys. Rev. 72 044302
46GaoFGuoF ZWenQ YZhuF C 2005 Phys. Rev. 72 036302
47QinS JGaoFWenQ YZhuF C 2007 Phys. Rev. 76 062324
48GaoFQinS JGuoF ZWenQ Y 2011 Phys. Rev. 84 022344
49WangT YLiY P 2013 Quantum Information Processing 12 1991
50HuangWYangY HJiaH Y 2015 Quantum Information Processing 14 2211
51ChangYXuC XZhangS BYanL L 2014 Chin. Phys. 23 010305
52LiC YZhouH YWangYDengF G 2005 Chin. Phys. Lett. 22 1049
53DengF GLiX HLiC YZhouPLiangY JZhouH Y 2006 Chin. Phys. Lett. 23 1676
54LiX HLiC YDengF GZhouPLiangY JZhouH Y 2007 Chin. Phys. Lett. 24 23
55ZhengCLongG F 2014 Science China Physics, Mechanics and Astronomy 57 1238
56LinT HHwangT 2014 Quantum Information Processing 13 917