† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant Nos. 11204156, 61178012, 11304179, and 11247240) and the Specialized Research Fund for the Doctoral Program of Higher Education of China (Grant No. 20133705110001).
We analyze universal conditions where the l1 norm and relative entropy of coherence are amplified and frozen under identical bit-flip channels; that is, using pre-measurements (quantum weak measurements or quantum measurement reversals) on the systems before undergoing local bit-flip channels. With the option of quantum weak measurements or quantum measurement reversals, the measurement strength and the success probability are all determined by the initial state of the quantum system.
Quantum coherence is a fundamental feature of quantum mechanics, describing the quantum interference phenomena of a quantum system. It has been widely used as a resource and root concept, such as quantum information processing,[1] quantum metrology,[2–5] entanglement creation,[6,7] thermodynamics,[8–12] and quantum biology.[13–16]
Only very recently have there been achievements towards developing a rigorous theory of coherence as a physical resource,[17–19] and necessary constraints have been put forward to assess the valid quantifiers of coherence.[17] A number of coherence measures based on various physical contexts have been put forward, such as the l1 norm of coherence and the relative entropy of coherence,[17] skew information,[20,21] and coherence measures based on entanglement.[22]
Quantum coherence is a useful physical resource but the coherence of a quantum state is often destroyed by noise. A challenge in exploiting the resource is to protect coherence from the decoherence caused by noise. Studies on this topic have been started in Ref. [23], where the authors found that the coherence measurements based on distances are frozen for some initial states of a quantum system undergoing local identical bit-flip channels. This finding illustrates that there exist such quantum states of which some coherence measures remain constant in certain noisy channels. However, the conditions of frozen coherence are not same for single qubit and multi-qubit and nontrivial universal freezing of the relative entropy of coherence is impossible for the dynamics of a single qubit under paradigmatic incoherent maps. Then, we ask whether there is a universal method to amplify and freeze coherence for single-qubit and multi-qubit, and for the l1 norm and the relative entropy of coherence measure.
Intuitively, both coherence and entanglement capture the quantumness of a physical system, and it is well known that entanglement stems from the superposition principle, which is also the essence of coherence. In practice, decoherence can severely undermine the quantum features in quantum information processing, and quantum entanglement is fragile to environmental noises. An idea is proposed to protect quantum states and quantum entanglements from decoherence using a weak measurement and measurement reversal.[24,25] Recently, reference [26] proved that using a weak measurement and measurement reversal can suppressing the amplitude damping decoherence.
Therefore, we can optimize quantum states and freeze coherence from decoherence using a weak measurement and measurement reversal.
The rest of this paper is organized as follows. In Section 2, we briefly discuss the measures of quantum coherence used in this study, describe the methodology for investigating their dynamics in the presence of local noise, introduced the weak measurement and quantum measurement reversal. In Section 3, we conclude the necessary and sufficient conditions for amplifying and freezing the quantum coherence of quantum systems undergoing local identical bit-flip channels using a weak measurement and measurement reversal. Section 4 compares the different methods of using measurement to protect the quantum coherence and entanglement when a quantum system undergoes incoherent channels. Section 5 contains the concluding remarks.
We first need to review some notions, such as incoherent states, incoherent operations, and coherence measures. For an N-qubit system associated with a Hilbert space C2N, we fix the computational basis {|0〉, |1〉}⊗N as the reference basis, and we define incoherent states as those whose density matrix δ is diagonal in such a basis,
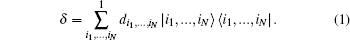
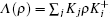
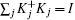

We will consider paradigmatic instances of incoherent channels that embody typical noise sources in quantum information processing,[1,17] whose action on a single qubit is described as follows, in terms of a parameter q ∈ [0,1], that encodes the strength of the noise and depends explicitly on time t. The bit-flip, bit + phase-flip, and phase-flip channels are represented in Kraus form by
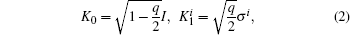
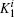
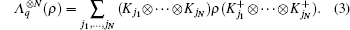
We now recall known measures of coherence.[17] The l1 norm quantifies coherence in an intuitive way via the off-diagonal elements of a density matrix ρ in the reference basis 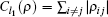
Theoretically, a weak measurement on a qubit can be done by monitoring its environment via an ideal detector. Whenever there is an excitation in the environment, the result is discarded. In the case of no excitation, the qubit state is just renormalized and allowed to evolve. The null-result weak measurement on a qubit maps as follows:
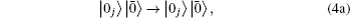
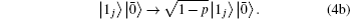
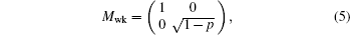
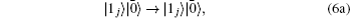
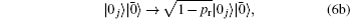
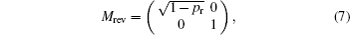
We now analyze conditions such that the l1 norm and the relative entropy of coherence are all invariant during the evolution of a quantum system under any of the noisy channels Λq described above.
Bromley et al. proved that only the bit and bit + phase-flip channels allow for nonzero frozen coherence (in the computational basis), while all the other considered incoherent channels leave coherence invariant only trivially when the initial state is already incoherent.[23] We focus our attention on the bit-flip channel.
For a single-qubit state in general as ρ = (I + ∑jnjσj)/2, in terms of its Bloch vector
We consider a single-qubit pure state
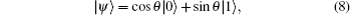
We now analyze the universal freezing of coherence for specific initial states (excluding the θ = {0,π/4,π/2,3π/4,π} in the above state, only n2(0) = 0) under bit-flip channels using a prior weak measurement or prior measurement reversal.
On the one hand, we perform prior weak measurements on a single-qubit state |ψ〉 = cosθ|0〉 + sinθ|1〉, and the initial state of the qubit becomes

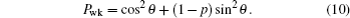
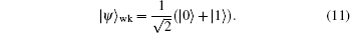
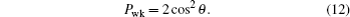
On the other hand, we perform a prior measurement reversal operator on a single-qubit state |ψ〉 = cosθ |0〉 + sinθ |1〉, the state of the qubit becomes
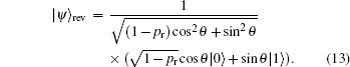
The success probability is
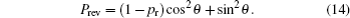
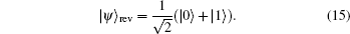
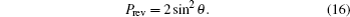
We now consider a single-qubit mixed state ρ = (I + ∑j njσj)/2, and assume its Bloch vector is 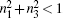
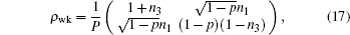
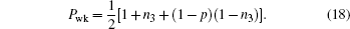
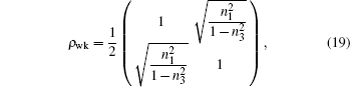
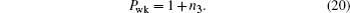
On the other hand, we perform prior measurement reversal operator on one qubit of state ρ and the state of the qubit becomes
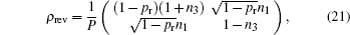
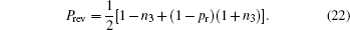
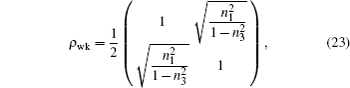
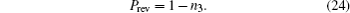
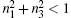
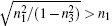
In conclusion, when using prior weak measurements or prior measurement reversal, nontrivial universal freezing of coherence is possible for the dynamics of a single qubit under paradigmatic incoherent maps. Furthermore, this method can amplify the coherence of the state.
We will show that the l1 norm and relative entropy of coherence manifest freezing forever in the case of two qubits undergoing local identical bit-flip channels starting from conditions of using prior weak measurements or prior measurement reversals.
For two-qubit states with maximally mixed marginals (M32 states), also known as Bell-diagonal states,[27] which are identified by a triple 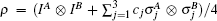
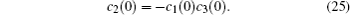
We consider the two-qubit Bell-like state
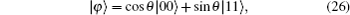

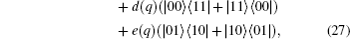

If θ = {0,π/2,π}, then the initial state is the incoherent state, the evolved state is also an incoherent state. If θ = {π/4,3π/4}, then the initial state is the Bell state c2(0) = −c1(0)c3(0) = −1. The state coherence is frozen for both coherence measurements under bit-flip channels, if θ is other values that manifest frozen coherence as measured by Cl1 under local bit-flip channels; however, the same does not hold for Cr.[23]
We apply prior weak measurements or prior measurement reversals in specific initial states |φ〉 (excluding θ = {0,π/4,π/2,3π/4,π}) to realize the freezing of the coherence of both coherence measurements under bit-flip channels. We perform prior weak measurements on one qubit of state |φ〉 = cosθ |00〉 + sinθ |11〉, and the initial two-qubit state becomes
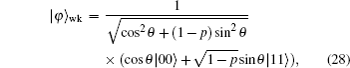
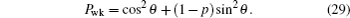

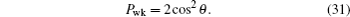
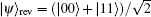
As can be seen from above, using prior weak measurements or prior measurement reversals, the two-qubit state can be amplified and frozen into the coherence of both coherence measurements under local identical bit-flip channels.
We will show that both measurements of quantum coherence manifest freezing forever in the case of N qubits undergoing local identical bit-flip channels on the conditions of using prior weak measurements or prior measurement reversals.
For N-qubit states
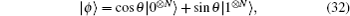
For θ ∈ (π/4,π/2) or θ ∈ (π/2,3π/4), we perform prior weak measurements on one qubit of state |ϕ〉 = cosθ|0⊗N〉 + sinθ|1⊗N〉, and the initial N-qubit state becomes
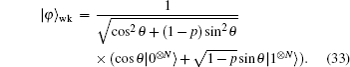
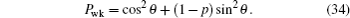
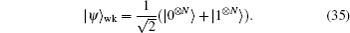

Similarly to single qubit case, for θ ∈ (0,π/4) or θ ∈ (3π/4,π), we perform a prior measurement reversal on one qubit of state |ϕ〉 = cosθ|0⊗N〉 + sinθ|1⊗N〉. When p = 1−tan2θ, the state becomes 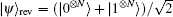
Similar to one qubit and two qubits, using prior weak measurements or prior measurement reversals, the l1 norm and relative entropy of coherence can be amplified and frozen forever in the case of N qubits undergoing local identical bit-flip channels.
Quantum coherence and quantum entanglement are all useful physical resources; furthermore, they are often destroyed by noise. The amplifying and freezing conditions established here for coherence have been identified. Now, we need to determine if these conditions can promote and protect entanglement. Focusing on the two-qubit case for clarity, we note the state |φ〉 = cosθ |00〉 + sinθ |11〉, using prior weak measurements on the one qubit of state |φ〉, we let the two-qubit enter the bit-flip channels. If θ ∈ (0,π/4) or θ ∈ (3π/4,π), when p = 1 − tan2θ, the state evolves to
It is thus evident that coherence is easier to control and protect than entanglement when the qubits undergo identical bit-flip channels. Therefore, quantum coherence may be a more useful physical resource than entanglement for performing communication and computational tasks.
We have determined conditions that any coherence measurements of quantum coherence are dynamically amplified and frozen. This occurs for an arbitrary number of qubits, initialized in a particular class of states using the pre-measurements (weak measurements or quantum measurement reversals) on one qubit of the quantum states before undergoing local independent and identical nondissipative flip channels. We find that the option of quantum weak measurements or quantum measurement reversals is determined by the initial state and the measurement strength is also determined by the initial state of the quantum system. We have shown that general agreements on amplifying and freezing conditions are both for the l1 norm and the relative entropy of coherence. These universal freezing conditions ensure a durable physical exploitation of coherence, regardless of how it is quantified. It will be interesting to explore the practical realizations of such dynamical conditions. Compared with increasing entanglement and trapping conditions by using the weak measurement and quantum measurement reversal, we can conclude that quantum coherence may be a more useful physical resource than entanglement.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 |


