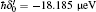† Corresponding author. E-mail:
‡ Corresponding author. E-mail:
Project partially supported by the National Natural Science Foundations of China (Grant Nos. 11374039 and 11174042) and the National Basic Research Program of China (Grant Nos. 2011CB922204 and 2013CB632805).
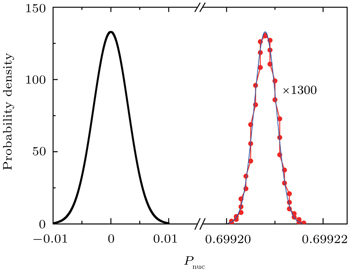
Hyperfine interaction between electron spin and randomly oriented nuclear spins is a key issue of electron coherence for quantum information/computation. We propose an efficient way to establish high polarization of nuclear spins and reduce the intrinsic nuclear spin fluctuations. Here, we polarize the nuclear spins in semiconductor quantum dot (QD) by the coherent population trapping (CPT) and the electric dipole spin resonance (EDSR) induced by optical fields and ac electric fields. By tuning the optical fields, we can obtain a powerful cooling background based on CPT for nuclear spin polarization. The EDSR can enhance the spin flip–flop rate which may increase the cooling efficiency. With the help of CPT and EDSR, an enhancement of 1300 times of the electron coherence time can be obtained after a 10-ns preparation time.
The dynamics of nuclear spins in semiconductor quantum dot (QD) and their coupling to electron spins is fundamentally different from that in semiconductor bulk or quantum well structures due to the increased fluctuations from the strong localization of the electron wave function. A single electron in QD interacts with about 105∼106 nuclei and this interaction has been identified as the main source of electron spin decoherence. However, its insensitivity to electron noise has been also noted. Therefore, electron spin degrees of freedom are widely considered to be promising candidates for storing information. The nuclear spin bath itself, with long nuclear spin coherence time, could be turned into an asset, such as a resource for quantum computation and quantum memories.[1,2] The manipulation of the nuclear spins will not only help us to understand the fundamental physics, but also directly improve the coherence time of electron spins.[3–7]
A number of experimental[8–10] and theoretical[11–16] studies reveal that the predominant decoherence mechanism in QD is the hyperfine coupling between the electron spin and the nuclear spins in the host material. To suppress the decoherence effects, one may either establish highly polarized nuclear spin states or nuclear spin states with narrow distribution of the polarization.[16] One basic approach to suppress the nuclear spin fluctuation is the feedback control by coupling the nuclear spins to a “background” of electron spin in specific configuration. One effective way of preparing such electron “background” for cooling the nuclear spins is to use the coherent population trapping (CPT), which is at the heart of a number of key advances in quantum optics.[17–22] Two circularly polarized laser fields/lights tuned to satisfy two-photon resonance could be used to deterministically prepare a nuclear-spin environment with ultranarrow Overhauser-field (OF) distribution by using CPT.[23–26] In turn, polarized nuclear spins induce an energy shift of the electron spin states, which can be described as an effective magnetic (Overhauser) field. Under a large (effective) magnetic field, the direct electron–nuclear flip–flop processes are strongly suppressed due to the large mismatch in the electronic and nuclear Zeeman splitting, which reduces the “cooling” efficiency.
In this paper we propose to use two optical fields to realize CPT with fixed electron spin polarization, which leads to highly polarized nuclear spin. In addition, we add an ac electric field to realize electric dipole spin resonance (EDSR),[27–30] which may increase the cooling efficiency by compensating the energy difference of electron states with different spins and enhancing the electron–nuclear spin flip–flop rate. Compared with the electron-spin-resonance with time-dependent magnetic field, the EDSR promises higher efficiency and strong local electric fields are easier to obtain than strong local magnetic fields. The EDSR enhanced feedback control of the nuclear spin bath (dynamical nuclear spin polarization) leads to interesting physics, such as the nontrivial dependence on the static magnetic field, the new condition of dark state, and the multiple ways to reach the dark state. By the combination effects of the optical fields and the ac electric fields, we are able to greatly prolong the electron spin decoherence time of 1300 times.
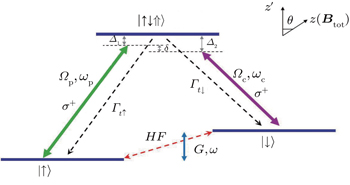
We explore the feedback control of the nuclear spin bath in a semiconductor QD, which includes the nuclear spin states, the Zeeman-split electron ground states and the negatively charged exciton (trion) |t〉 = | ↑↓⇑〉 (| ↑〉, |↓〉, |⇑〉 the electron spin-up, spin-down states and heavy hole state with Jz′ = 3/2). We manipulate the electron–nuclear dynamics by the optical fields and an ac electric field. The lowest electronic states in a QD formed in GaAs semiconductor are optically active under σ+ circularly polarized excitation. |t〉 = | ↑↓⇑〉 is the only optically excited state (transitions to Jz′ = −3/2 are forbidden due to the optical selection rules) (Fig. 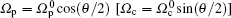


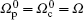
A large magnetic field in the order of Tesla is applied to suppress the dipole interaction among nuclear spins.[7,31] The large magnetic field
The Hamiltonian for the system of coupled electron spin-nuclear spin is H = H0 + Hlaser + Hhf + Hel. Here
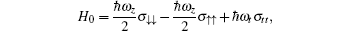
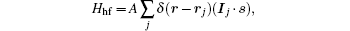
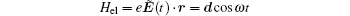
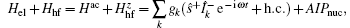
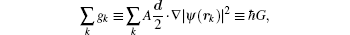
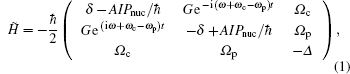

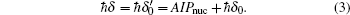
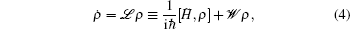
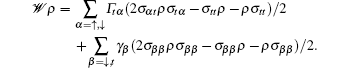
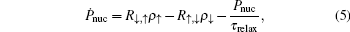
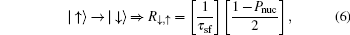
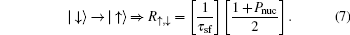

In this section, we present our results on the condition of dark state and the dynamic of nuclear spins when we change the direction of the magnetic field. The nuclear spin fluctuation suppression modulated by the optical fields and the ac electric field will be discussed in detail. In our system, the two laser fields may generate an electron dark state of fixed electron spin components, which provides the nuclear spin cooling background. The ac electric field leads to EDSR, which may enhance the cooling efficiency by increasing the effective spin flip–flop rate.
We first consider the electron dark state. Under the condition of the dark state, the electron spin arrives at the dark state and the nuclear spin polarization reaches the value set by electron spin polarization in the long time limit. In other words, 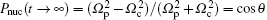
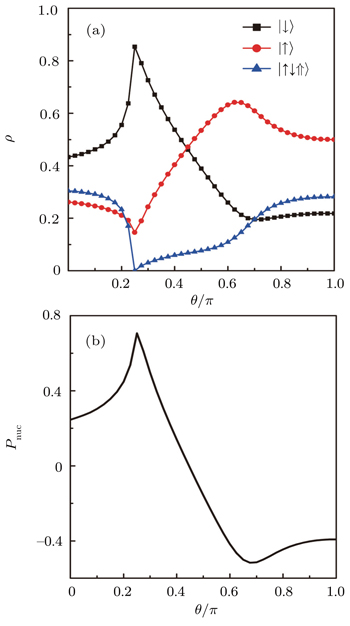
In general, the electron spin state population will change with the rotation of the magnetic field as shown in Fig.
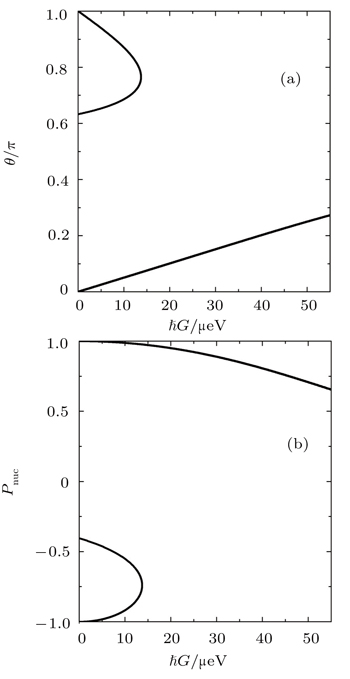
Then, we analyze the condition of dark state versus the Rabi frequency G induced by the ac electron field theoretically. Through the above analysis, we know that the θ should fit the equation 
Figure
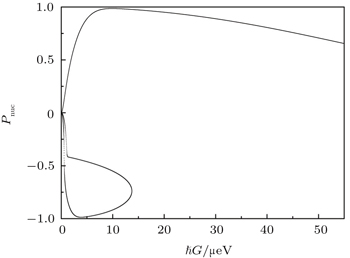 | Fig. 4. The nuclear polarization after a preparation time of 100 ns under the condition of dark state. The parameters are the same as those in Fig. |
The very low nuclear spin polarization for very small ħG is due to the weak effective interaction between electron and nuclear spins. But if the ħG is too large (the cooling efficiency is good enough), the polarization of electron spin states is not too high (the background is not “cold” enough), which will lead to rapid decline of nuclear spin polarization. Therefore, there is an optimal ħG for achieving a highly polarized nuclear spin state.
Under experimentally achievable temperature, the nuclear spin orientation in a thermal distribution is highly random because of its small energy scale. Thus, the configurations of the nuclear spin bath have large statistical fluctuations, which give rise to a large inhomogeneous broadening of statistical distribution of the nuclear spins. In a large external magnetic field, the statistical fluctuations of the nuclear spins give rise to pure dephasing of the electron spin. We assume a Gaussian distribution of the nuclear spins 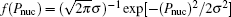
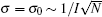
We have studied the electron spin-nuclear spin dynamics in the presence of optical fields and ac electric fields, paying particular attention to the dependence of the direction of the static magnetic field. We have found the general condition of dark state, which provides the efficient cooling background. By using CPT (induced by the optical fields) and EDSR (induced by the ac electron fields), we can have the electron spin dark state and polarize the nuclear spins through the interaction between electron spin and nuclear spins. We are able to find the optimal condition to obtain the highly polarized nuclear spins with much narrower distribution width. This cooled nuclear spin background is very useful in the enhancement of electron spin coherent time, which is at the forefront of quantum computation and quantum information.[4–7]
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 |