† Corresponding author. E-mail:
Project supported by the National Natural Science Foundation of China (Grant No. 11364028), the Major Projects of the Natural Science Foundation of Inner Mongolia Autonomous Region, China (Grant No. 2013ZD02), and the Project of “Prairie Excellent” Engineering in Inner Mongolia Autonomous Region, China.
The polaron effect on the optical rectification in spherical quantum dots with a shallow hydrogenic impurity in the presence of electric field is theoretically investigated by taking into account the interactions of the electrons with both confined and surface optical phonons. Besides, the interaction between impurity and phonons is also considered. Numerical calculations are presented for typical Zn1−xCdxSe/ZnSe material. It is found that the polaronic effect or electric field leads to the redshifted resonant peaks of the optical rectification coefficients. It is also found that the peak values of the optical rectification coefficients with the polaronic effect are larger than without the polaronic effect, especially for smaller Cd concentrations or stronger electric field.
Nonlinear optical properties in low-dimensional semiconductor nanostructures such as quantum wells, quantum wires, and quantum dots (QDs) have aroused much interest in the past few years.[1–16] In these systems, QDs can confine charge carriers in all spatial dimensions and their sizes, shapes, and other properties can be controlled experimentally. Furthermore, there exists a strong quantum confinement effect in QDs, which induces a dramatic enhancement in optical nonlinearities compared with bulk materials. This property leads to potential applications in electronic and optoelectronic devices.[17–19] Therefore, it is necessary to study the nonlinear optical properties of QDs due to their unique physical properties and their potential applications.
Because the electron–phonon interaction plays an important role in the nonlinear optical properties, the polaron effects on linear and nonlinear optical properties have been widely studied.[20–25] In nonlinear optical properties, nonlinear optical rectification (OR) in semiconductor heterostructure and nanostructure is a second-order nonlinear optical effect which is important for investigating their electronic structures. Due to the fact that the polaron effect can induce a very large enhancement effect, a lot of authors have devoted themselves to the issue about the polaron effect on the OR coefficient. For instance, Zhang and Guo[26] investigated the effect of the electron–phonon interaction on the OR in a semi-parabolic quantum well and found that the electron–phonon interaction increases the OR up to a factor of 6–13. Wu et al.[27] investigated the polaron effect on nonlinear OR in asymmetrical Gaussian potential quantum well, and revealed that the OR coefficients are strongly dependent on the confinement potential and the electric field, and greatly enhanced by considering the polaron effect. Xiao et al.[28] investigated the polaron effect on the OR in an asymmetrical semi-exponential quantum well, and they reported that when considering the electron-LO-phonon, the resonant peak of the OR is enhanced, and the blue shifts are also observed. Liu et al.[29,30] studied the polaron effect on the OR in cylindrical quantum dots in the presence of electric and magnetic fields and found that the OR coefficient is greatly enhanced, with the polaron effect taken into account. All relative research results reveal that electron–phonon interaction plays a very important role in nonlinear optical properties.
Due to the difference in the dielectric constant of the material between inside and outside the QDs, besides the confined optical (CO) phonons, there exist surface optical (SO) phonons in the structure, and it depends strongly on the QD shape and electric field.[31] In some investigations, the QD shapes were approximated as various forms: cylinders,[29,30] cones,[32] lens,[33,34] pyramids,[35] ellipses,[36,37] spheres,[38–40] and the polaronic effect has been studied in some works. Unfortunately, in most of the research mentioned above the impurity–phonon interaction is either ignored or not discussed. In fact, the contribution from impurity–phonon interaction is very important and generally larger than that from electron–phonon interaction.[41,42] To the best of our knowledge, there are fewer research studies related to the polaron effect on the OR in spherical quantum dots with taking into account both electron–phonon and impurity–phonon interaction. For these reasons, the polaron effect is important to the OR of QDs and should be considered in the relevant work.
In this paper, polaron effect on the OR in a spherical quantum dot in the presence of the electric field is theoretically investigated by using a variational approach, with the electron–phonon and impurity–phonon interactions taken into account, including CO and SO phonon modes. To make it closer to the real situation, the electronic confinement is modeled by a finite potential well. The rest of this paper is organized as follows. In Section 2, the electron–phonon interaction and the nonlinear OR coefficients are described. In Section 3, the numerical results and discussions are performed. Finally, some conclusions are briefly drawn from the present study in Section 4.
We consider the electron interacting with the optical phonons in a spherical quantum dot comprised of Zn1−xCdxSe/ZnSe with radius R. When the electron is inside (r < R) the QD, it will interact with the internal LO phonons, we call it CO phonons. When the electron is close to the QD boundary (r ≈ R), it will interact with the SO phonons. Within the framework of effective mass approximation, the Hamiltonian of the system in the presence of an applied electric field along the z direction is given by
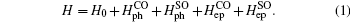

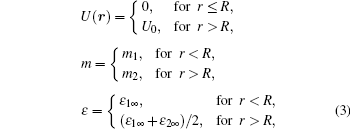



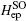
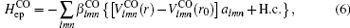
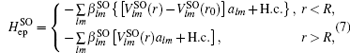
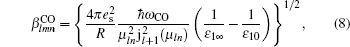


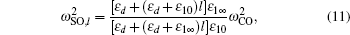

Firstly, it is necessary to eliminate the contribution of the impurity–phonon interactions to the total electron energy. It can be obtained by using a first unitary transformation to displace the equilibrium position of the ions as follows:

Subsequently, the Hamiltonian can be transformed into the following form:


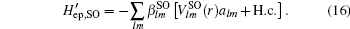
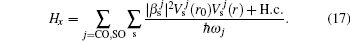
The effect of the electron–phonon interaction is to displace further the equilibrium positions of the ions within the adiabatic approximation. This can be obtained by the following unitary transformation:



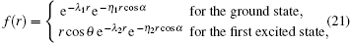

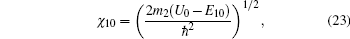

After some calculations, the expectation value of the system Hamiltonian in the phonon–vacuum state is given by



Finally, inserting Eqs. (
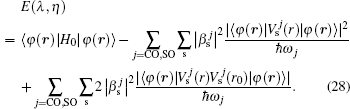
The analytical expression for the nonlinear optical rectification coefficient can be obtained by a density matrix approach and an iterative procedure[46,47]
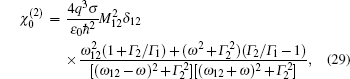
The maximum value of 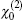

In this section, we will discuss the OR coefficients in a spherical quantum dot with the electric field in the presence of the electron–phonon and impurity–phonon interactions. The parameters used in our calculations are as follows:[48–50] σ = 5.0 × 1024 m−3, nr = 2.4, T1 = 1 ps, T2 = 0.1 ps; m1 = 0.13m0, ε10 = 9.3, ε1∞ = 6.1 for CdSe; m1 = 0.171m0, ε10 = 8.33, ε1∞ = 5.9, εd = 2.25 for ZnSe, where m0 is the bare electron mass. The parameters for Zn1−xCdxSe are obtained by linear interpolation from the corresponding values for ZnSe and CdSe. The value of the conduction band offset U0 is assumed to be 80% of bandgap mismatch.[43]
In Fig. 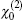
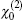
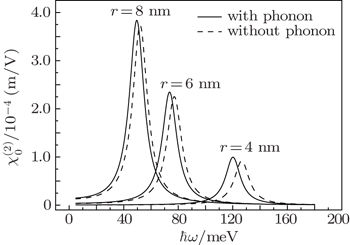 | Fig. 1. Variations of OR coefficient 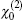 |
Figure 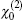
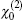
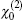

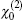


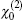
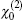
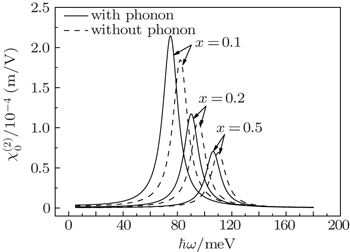 | Fig. 2. Plots of OR coefficients 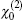 |
 | Fig. 3. Variations of geometrical factor  |
Figure 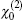
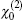

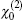
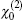
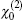


 | Fig. 4. Variations of OR coefficient 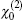 |
In this paper, we study theoretically the polaron effect on the OR in a Zn1−xCdxSe/ZnSe spherical quantum dot with electric field in detail, with the electron–phonon and impurity–phonon interactions taken into account. Our calculations mainly focus on the dependences of the OR on external electric field F, Cd concentration x, and QD radius R. The calculated results show that the polaronic effect or electric field leads to the redshifted resonant peaks of the OR coefficients. Our result also reveals that the peak values of 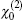
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 |



