† Corresponding author. E-mail:
The Monte Carlo simulation is used to investigate the magnetic properties of ferromagnetic superlattices through the Ising model. The reduced critical temperatures of the ferromagnetic superlattices are studied each as a function of layer thickness for different values of exchange interaction. The exchange interaction in each layer within the interface and the crystal field in the unit cell are studied. The magnetic coercive fields and magnetization remnants are obtained for different values of exchange interaction, different values of temperature and crystal field with fixed values of physical parameters.
Magnetism in ultrathin film is now a fairly well established field of research, and has attracted much attention, both experimentally and theoretically.[1–4] The magnetic properties of hexagonal compact superlattices of materials A and B: a helimagnetic and a ferromagnetic phase, at low temperature, were studied in Ref. [5]. The ferromagnetic/antiferromagnetic superlattices, which are composed of a spin-1/2 ferromagnetic monolayer and a spin-1 antiferromagnetic monolayer with a single-ion anisotropy, respectively, have been investigated in Ref. [6]. The magnetization in (Fe 3 nm/Dy 2 nm) multilayers have been studied experimentally and numerically in Ref. [7]. The influences of the exchange coupling and single-ion anisotropy parameters in the model Hamiltonian on the martensitic–austenitic transformations were studied and analyzed in comparison with the results for hexagonal nanoparticles in Ref. [8]. To analyze the dependence of the critical temperature TC on size, some authors[9–13] have considered the ferromagnetic nearest-neighbor Ising model of the simple cubic lattices for film of c layer. The magnetic coupling at the surface, JS, may be identical with or different from that in the bulk, Jb. Transition temperature of a multilayer consisting of spin-1/2 and spin-3/2 ferromagnetic Ising layers has been computed by using the effective field theory[14–16] in order to explain the experimental data of rare earth/transition metal multilayer films, respectively. Mean-field theory has also been used to study magnetic properties of rare earth/transition multilayers,[17] but very few Monte Carlo studies dealt with the rare earth/transition metal multilayer systems. The phase transition and magnetic properties of a ferromagnet spin-S, a disordered diluted thin and semi-infinite film with a face-centered cubic lattice are investigated by using the high temperature series expansions technique extrapolated with Padé approximants method for Heisenberg, XY and Ising models in Ref. [18]. The magnetic properties of ferromagnetic Ni/Au core/shell have been studied by using Monte Carlo simulations within the Ising model in Ref. [19]. Hysteresis loops, micromagnetic structures, and hysteresis loop area curves, as well as dynamic correlation between the magnetization and the external field have been studied each as a function of the field and film parameters in Ref. [20]. Recently, we have used the Monte Carlo simulations to study the magnetic properties of a nanowire system based on a honeycomb lattice in the absence and presence of both an external magnetic field and crystal field.[21] The purpose of this work is to explore the variations of magnetization and magnetic susceptibility with the reduced temperature, exchange interaction between bilayers and zero crystal field for a fixed value of exchange interaction in surface and in bulk with different sizes. The critical temperatures are obtained for different values of size la and for different values of exchange interactions between bilayers. The magnetic hysteresis cycle with reduced crystal field, exchange interaction between bilayers and reduced critical temperatures are established. From these curves we deduce the coercive field and magnetization remnant.
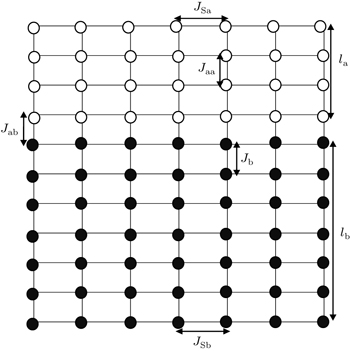
We consider superlattices of ferromagnetic materials a and b, with a simple cubic structure. The la and lb are the corresponding numbers of atomic layers in materials a and b, respectively. l = la + lb is the thickness of the unit cell (see Fig.
The Hamiltonian for the a and b ferromagnetic superlattices includes the interactions between the nearest neighbors, external magnetic field, and the crystal field is given as
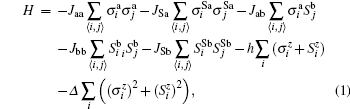
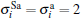

The ferromagnetic materials a and b superlattices are assumed to reside in the unit cells and the system consists of the total number of spins N = (la + lb)l, with l = 8, lb = 7 and la = 5, 7, 9, 11 where (la + lb) is the system size as given in Fig.
the magnetization of superlattices
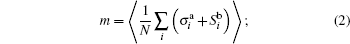
the internal energy E per site
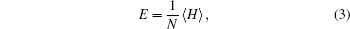
the magnetic susceptibility
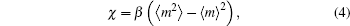
The superlattices of ferromagnetic materials a and b are investigated by Monte Carlo simulation. The transition temperatures each as a function of surface exchange constant are studied. Figure
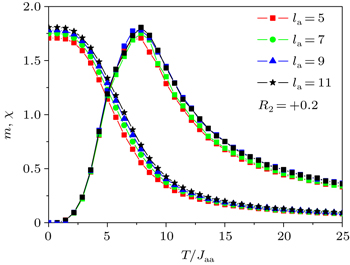 | Fig. 2. Variations of magnetization and magnetic susceptibilities with reduced temperatures T/Jaa for R2 = 0.2 with Δ/Jaa = 0.0 and h/Jaa = 0.4. |
Figure
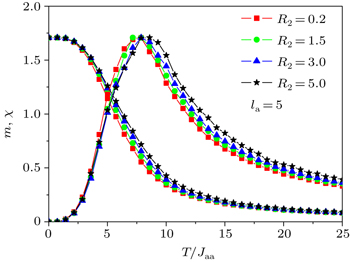 | Fig. 3. Variations of magnetization and magnetic susceptibility with reduced temperature T/Jaa for R2 = 0.2, 1.5, 3, 5 with Δ/Jaa = 0.0 and h/Jaa = 0.4. |
Figure
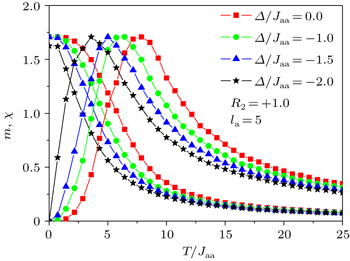 | Fig. 4. Variations of magnetization and magnetic susceptibilities with reduced temperature T/Jaa for Δ/Jaa = 0.0, −1.0, −1.5, −2.0, R2 = 1, h/Jaa = 0.4, and la = 5. |
 | Fig. 5. Variations of magnetization with reduced exchange interaction R2: (a) for Δ/Jaa = 1.0, 1.5, 2.0, 2.5, la = 7 and (b) for la = 5, 7, 9, 11, T/Jaa = 1.5, and h/Jaa = 0.4. |
| Table 1. Values of reduced critical temperatures for different values of crystal field Δ with la = 5 and R2 = 1. . |
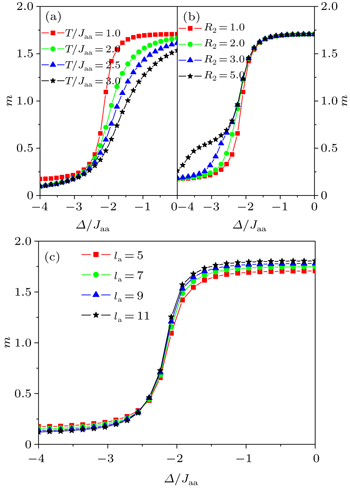
The variations of magnetization with reduced crystal field Δ/Jaa for (T/Jaa = 1, 2, 2.5, 3, R2 = 1 and la = 5), for (R2 = 1, 2, 3, 5, T/Jaa = 1 and la = 5) and for (la = 5, 7, 9, 11, T/Jaa = 1 and R2 = 1), are given in Figs.
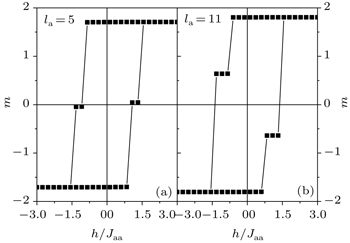
The magnetic hysteresis cycles with the reduced exchange interactions R2 = 0.4, 3.0, for a zero reduced crystal field and T/Jaa = 1 are shown in Figs.
 | Fig. 7. Magnetic hysteresis cycles with the reduced exchange interaction R2 = 0.4 (a), 3.0 (b) for a zero reduced crystal field, T/Jaa = 1 and la = 5. |
 | Fig. 8. Magnetic hysteresis cycles with the reduced crystal field Δ/Jaa = 0.0 (a), −1.0 (b) for R2 = 0.4, T/Jaa = 3, and la = 5. |
The Monte Carlo simulations are used to investigate the magnetic properties of the Ising model of infinite a and b ferromagnetic superlattices having simple cubic crystal structure. The effects of the reduced interlayer exchange coupling R2, crystal field and the thickness of the unit cell on a and b ferromagnetic superlattices are given. The transition temperatures as a function of exchange interaction constants and crystal field are calculated. The obtained values are comparable to those given by the other theoretical results. The coercive field and the remnant magnetization have no influence when increasing the reduced exchange interaction R2. The coercive field decreases with increasing the reduced crystal field and increases with increasing the size of the system.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 |