† Corresponding author. E-mail:
Particle swarm optimization (PSO) and invasive weed optimization (IWO) algorithms are used for extracting the modeling parameters of materials useful for optics and photonics research community. These two bio-inspired algorithms are used here for the first time in this particular field to the best of our knowledge. The algorithms are used for modeling graphene oxide and the performances of the two are compared. Two objective functions are used for different boundary values. Root mean square (RMS) deviation is determined and compared.
The dielectric materials play an important role in optical devices. The permittivity values of all dielectric materials are frequency-dependent. In order to simulate real materials, it is required to incorporate the frequency dependent properties of the materials in a well-defined way whenever optical structures are expected to operate over a wide range of frequency. The well-known parametric models such as Debye model, Lorentz model, Lorentz–Drude model, modified-Debye model, Brendel–Bormann model, etc. can be used to generate such optical properties by fitting them to experimental data using nonlinear optimizer. Electromagnetic simulations with arbitrary geometries and inhomogeneous materials are often accomplished by using computational electromagnetic methods such as the finite difference time-domain (FDTD)[1] method in which the parametric models are required in order to integrate the dispersive properties of different materials. However, an efficient optimization technique is needed to extract the parameters of the different models to fit both the real and imaginary parts of the complex permittivity in order to reduce the computational cost and obtain accurate results.
Several optimization techniques have been used to model the frequency dependent properties of the materials in optical range. Researchers have been working on different novel materials with aiming to find out the precise modeling parameters using different models. Rakic et al.[2] determined the dielectric parameters for different metals by using Brendel–Bormann and Lorentz–Drude models through using simulated annealing algorithm technique.[2] Pernice et al. used an adaptive nonlinear least square algorithm to extract the parameters for metal.[3] Particle swarm least squares optimization technique was utilized by Kelley et al. to fit the Debye model function.[4] Saber et al.[5] used a genetic algorithm based technique for extracting optical parameters. Sagor et al.[6] presented a comparative study of the performances of different mathematical models for some materials. Other traditional and bio-inspired algorithms have also been used in this field by several researchers.[4,7–10]
Most of the efforts have been made to compare different material models by using single optimization methods. However, the comparison of different optimization techniques for a particular model to reduce the computational cost while using the material in different simulators is yet to be done. Recently, particle swarm optimization (PSO) and invasive weed optimization (IWO) have received increased interest in the field of optimization. These techniques have shown great ability in numerous real-world applications.[11–13] Researchers made a lot of efforts to compare these algorithms to validate that one algorithm outperforms another in a specified set of problems. However, to the best of our knowledge, a detail comparative study of different optimization techniques on complex material modeling has never been made before.
In this paper, we present a comparative study of PSO and IWO to extract the parameters for dielectric materials in optical range by using Debye model. The dielectric material used here is graphene oxide in a spectral range of 350 nm–800 nm. It is observed that the performances of IWO and PSO depend on the mathematical definition of the objective function used and also on the chosen boundary conditions. We work with two different objective functions and three different boundary conditions for each objective function. The observations show the relative suitability of the objective functions and the boundary conditions under different circumstances.
Several studies in the literature can be found where Debye function expansions of complex permittivity are considered.[4] The Debye model refers to dielectrics in terms of electric dipoles. The applied electric field causes the dipoles to respond accordingly. Oscillating frequency governs the polarization of the material.
The general equation for Debye model can be written as
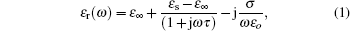
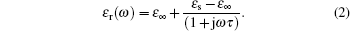
Kennedy and Eberhart introduced PSO in 1995.[15] It was inspired by the swarming behavior as displayed by a flock of birds, a school of fish, or even human social behavior influenced by other individuals.[16] It shows several similarities with evolutionary algorithm based optimization approaches, i.e. genetic algorithm (GA), especially in the case of population (particle) initialization. But unlike GA it does not employ any evolutionary operator like crossover and mutation while updating the population for the next iteration. The particles travel within a predefined search space and shifts closer to the optimal solution with each iteration.
PSO begins with a population of random solution in an N-dimensional constrained search space. The constraints are imposed on the solution space to mimic the limitation of real world scenario. The i-th particle of the population is represented by Xi = (xi1, xi2,…, xiN). Each particle keeps record of its location in the solution space associated with the fittest solution it has achieved thus far. The fitness value for particle ‘i’ is also stored as Pi = (pi1, pi2,…, piN). The global tracker of the PSO keeps the track of the overall best value and its corresponding location, obtained thus far by any particle in the population. In each iteration the velocity and position of particles are updated by the following relations:
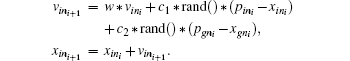
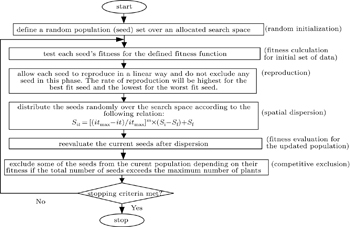
Invasive weed optimization (IWO) is a recent meta-heuristic search algorithm which is inspired from the weed colonizing technique. Mehrabian and Lucas introduced the concept in 2006.[17] It is a numerical stochastic optimization algorithm that replicates the natural behaviors of weeds in colonizing and finding suitable place for growth and reproduction. Some of the distinctive properties of IWO in contrary to other evolutionary algorithms are the manner of reproduction, spatial dispersal after reproduction and competitive exclusion. The working procedure of the IWO algorithm is provided here in the form of flow chart, as shown in Fig.
Graphene oxide is chosen for evaluating PSO and IWO by using Debye model. The experimental data of the complex permittivity of graphene oxide are obtained from Ref. [18] in a spectral range of 350 nm–800 nm. The performances of the optimization methods are evaluated by using two objective functions as follows:

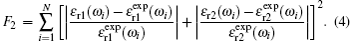
Boundary 1:
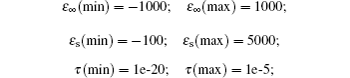
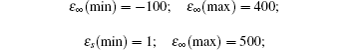


The experimental values of refractive index, n and extinction coefficient, k for graphene oxide at different frequencies are obtained from Jung et al.’s work.[18] From these values the real and imaginary parts of complex permittivity are calculated as follows:
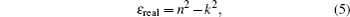

For different population sizes, the curves of fitness versus iteration number for different boundary conditions and objective functions are shown in Figs.
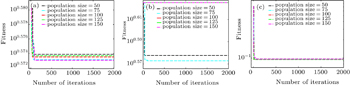 | Fig. 2. Variations of fitness with the number of iterations for different population sizes for IWO working with objective function 1 and boundary conditions (a) 1, (b) 2, and (c) 3. |
 | Fig. 3. Variations of fitness with the number of iterations for different population sizes for IWO working with objective function 2 and boundary conditions (a) 1, (b) 2, and (c) 3. |
 | Fig. 4. Variations of fitness with the number of iterations for different population sizes for PSO working with objective function 1 and boundary conditions (a) 1, (b) 2, and (c) 3. |
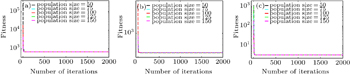 | Fig. 5. Variations of fitness with the number of iterations for different population sizes for PSO working with objective function 2 and boundary conditions (a) 1, (b) 2, and (c) 3. |
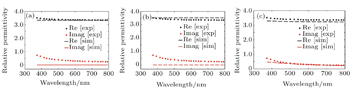 | Fig. 6. Comparisons between the experimental and fitted permittivities of graphene oxide for IWO working with objective function 1 and boundary conditions (a) 1, (b) 2, and (c) 3. |
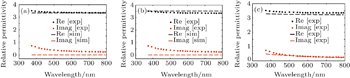 | Fig. 7. Comparisons between the experimental and fitted permittivities of graphene oxide for IWO working with objective function 2 and boundary conditions (a) 1, (b) 2, and (c) 3. |
 | Fig. 8. Comparisons between the experimental and fitted permittivities of graphene oxide for PSO working with objective function 1 and boundary conditions (a) 1, (b) 2, and (c) 3. |
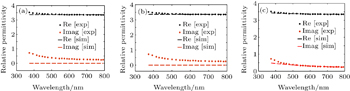 | Fig. 9. Comparisons between the experimental and fitted permittivities of graphene oxide for PSO working with objective function 2 and boundary conditions (a) 1, (b) 2, and (c) 3. |
From Table
| Table 1. Performance parameters of the PSO and IWO algorithms in optical parameter extraction for first objective function. . |
| Table 2. Performance parameters of the PSO and IWO algorithms in optical parameter extraction for second objective function. . |
From Table
For IWO working with the first objective function, the change in RMS deviation is very minute between boundary conditions 1 and 2. For the first boundary condition the RMS deviation is 0.0916 and for the second boundary condition it is 0.1308. But for the third boundary condition, it comes down to around 0.029. The objective function value remains within the range of 3.74–4.22 for the first two boundary conditions but decreases to around 0.0935 for the third boundary condition. So, for the first objective function, IWO performs better for boundary condition 3 which is the smallest boundary. This agrees with the common intuition that the smaller the search area, the easier it is to find the solution.
For the second objective function, a change in boundary condition in PSO does not cause any significant variation in the RMS deviation (it changes slightly around 0.073) and the value of the objective function (it remains within 685–690). So, for this objective function, the choice of boundary condition has no significant effect on the performance of PSO.
For IWO using the second objective function, it is observed that the RMS deviation (0.0916) for the first boundary condition is very close to those for the other two boundary conditions (for both these condition, the deviations are both 0.1308). Besides, the objective function value for the three boundary conditions remain within a range of 3.74–4.22. So, for IWO working with the second objective function, the choice of boundary condition has little effect on the performance of the algorithm, an observation which is similar to that for PSO working with the same objective function.
So, the use of the second objective function makes the performances of IWO and PSO less dependent on the chosen boundary conditions.
Moreover, we observe that for PSO, the function value for the first objective function is smaller (around 0.0965–3.74) than that for the second objective function (around 690) while the RMS deviations for the two are comparable, irrespective of the boundary condition. So, the performance of PSO is better if the first objective function is used.
For IWO, the two objective functions have comparable outputs for the first two boundary conditions. But as the boundary size in condition 3 decreases, the first objective function gives a much lower objective function value (around 0.0935) than the second one (around 3.74–4.22). So, for smaller boundaries, IWO performs better with the first objective function.
Furthermore, for the second objective function, it can be observed that there are no differences in RMS deviation and objective function value obtained for boundaries 2 and 3 for both PSO and IWO. This gives an indication that reducing the boundary size beyond a certain extent may have no effect on the optimization performance.
In this work, we choose single pole-pair Debye model over multi-pole pair models since it is found to be adequate to model the variation in permittivity of graphene oxide with reasonable accuracy. Besides, the use of a single pole-pair model would result in a smaller computational time. However, multi-pole pair models have to be used in the cases where a single-pole pair model is not able to provide reasonable optimization.
To the best of our knowledge, a comparative study of PSO and IWO in extracting optical parameters has not been published before. In this work we analyze the performances of these two algorithms for extracting the parameters required to model the frequency dependent permittivity of graphene oxide using single pole-pair Debye model for two different objective functions and three boundary conditions, thus working with six different sets of choices. After comparing the performance of the two algorithms, we find relative advantages of the objective functions for different choices. This study shows that both PSO and IWO are robust in extracting mathematical parameters required to model the experimental variation of permittivity of graphene oxide. Optical properties of other materials can also be replicated based on other models using these algorithms.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 |