† Corresponding author. E-mail:
‡ Corresponding author. E-mail:
Project supported by the National Basic Research Program of China (Grant No. 2012CB921504), the National Natural Science Foundation of China (Grant Nos. 11574148, 11474162, 1274171, 11674172, and 11674175), and the Specialized Research Fund for the Doctoral Program of Higher Education, China (Grant Nos. 20110091120040 and 20120091110001).
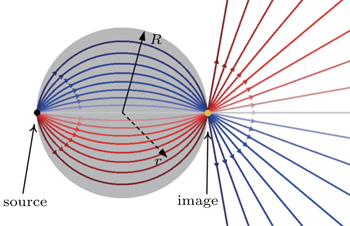
We have proposed a two-dimensional acoustic Maxwell’s fish-eye lens by using the gradient-index metamaterials with space-coiling units. By adjusting the structural parameters of the units, the refractive index can be gradually varied, which is key role to design the acoustic fish-eye lens. As predicted by ray trajectories on a virtual sphere, the proposed lens has the capability to focus the acoustic wave irradiated from a point source at the surface of the lens on the diametrically opposite side of the lens. The broadband and low loss performance is further demonstrated for the lens. The proposed acoustic fish-eye lens is expected to have the potential applications in directional acoustic coupler or coherent ultrasonic imaging.
Acoustic gradient index (GRIN) media in which the refractive index can be varied from point to point have received intensive interest for its significant applications in ultrasonic medical instruments, secret communication, acoustic detection, etc.[1–4] Rather than the conventional material, acoustic GRIN media show a spatial variation of the refraction index and then could flexibly manipulate acoustic wave in a variety of circumstances. Although acoustic GRIN media have significant potential advantages, they are far less prevalent in practical applications due to the fact that there are still challenges in the practice fabrication. Recent advances in acoustic metamaterials have promised a way to realize unusual material parameters unavailable in nature, giving the possibility in designing novel devices such as acoustic cloak,[5–7] superlens,[8–10] hyperlens,[11,12] and GRIN lens.[13–21] For example, it has been demonstrated that a metamaterial-based acoustic GRIN lens could modify sound radiation patterns with a deep-subwavelength thickness range.[14] Based on tapered labyrinthine metamaterials, Xie et al. also experimentally demonstrated an acoustic metasurface capable of general wavefront modulation.[15]
Among different GRIN devices with fascinating features, an optical Maxwell’s fish-eye (MFE) lens is of special interest, in which a gradient of decreasing refractive index is radially out from the lens center and a point source located at the edge of the lens can be focused on the diametrically opposite side.[22,23] Recently, Liu et al. have implemented an optical MFE lens with an ideal index gradient based on a two-dimensional (2D) inhomogeneous artificial dielectric medium.[24] A thickness-variations-based MFE lens for flexural wave in a thin plate has been further proposed and demonstrated by simulations.[25] Subsequently, Lefebvre et al. experimentally demonstrated the MFE lens for flexural wave based on a thin duraluminium plate with varying thickness.[26] It would be of interest to generalize the concept of the MFE lens to acoustic wave, which may offer opportunities in application in directional acoustic coupler or coherent ultrasonic imaging.
In this paper, we have proposed a 2D acoustic Maxwell’s fish-eye (AMFE) lens by using the space-coiling acoustic metamaterials (SAM) with a radius-dependent gradient refractive index. The numerical results show that the proposed lens can successfully function as an AMFE lens and has the capability to image the acoustic wave irradiated from a point source located at its surface to the diametrically opposite side of the lens. The broadband and low loss performance of the lens is further demonstrated.
The conventional 2D AMFE lens can be shown by a cylindrical lens of a radius R, in which the refraction index varies according to the corresponding spatial position, n = 2/[1+(r/R)2], (0 ≤ r ≤ R), where r is the distance from the observing point to the lens center. Figure
We continue to realize the 2D AMFE lens by using the SAM, which has been proposed[27] and used in the design of metamaterial devices such as the GRIN lens.[18,28] Here, the SAM is adapted as the fundamental unit to compose the AMFE lens, as illustrated in Fig.
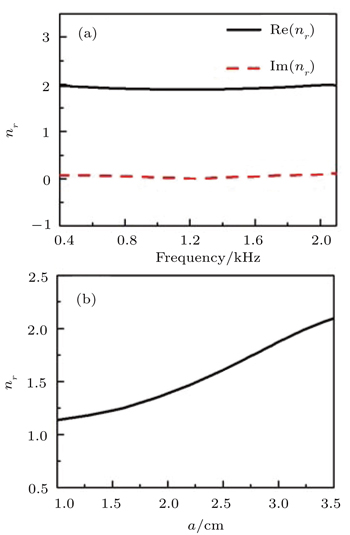
At low frequency, the SAM unit can be treated as an effective medium, which can be characterized by the relative effective refractive index nr and the relative effective acoustic impedance Zr. nr and Zr can be obtained by a standard retrieval procedure.[29] Note that the scalar sound waves propagate along the zigzag channels instead of a straight line from the inlet to the outlet. Correspondingly, the propagating phase should be heavily delayed and the extent of phase delay is dependent on the SAM structure. The space is effectively coiled up and the acoustic propagation becomes effectively slow when the wave passes through the SAM. Therefore, by adjusting the structural parameters of the SAM unit, nr can be easily modulated and then the gradually-varied refractive index that the AMFE lens needed can be flexibly obtained. It is noted that nr should be enhanced by adding more folds into the unit. Thus the SAM may have great potential application in tunable materials.
Figure
Figure
The desired AMFE lens has a cylindrical symmetry, where the refractive index is required to be equal at each circle with the same radius. However, due to the square profile of the SAM unit, we have to make discretization in the whole circular region and arrange the units properly according to the requirement of the refractive index. As a particular example, we choose R = 40 cm. In theory, the more finely the profile is discretized, the better the performance of the lens. Here, the designed lens is finally discretized in 10 rings of the SAM and hence the spacing between two neighbouring rings in the radial direction is 4 cm. Figure
Figure
 | Fig. 5. Schematic view of the proposed AMFE lens. The proposed AMFE lens is fabricated by gradually decreasing the a-value, and the total number of the SAM units is 289. |
We have further performed the full-wave simulations to describe the acoustic property of the AMFE lens by using a finite-element method. Figure
 | Fig. 6. Distribution of the simulated acoustic pressure fields for the AMFE lens: (a) f = 1 kHz, (b) f = 1.5 kHz, and (c) f = 2 kHz, in which the solid circle indicates the boundary of the lens. |
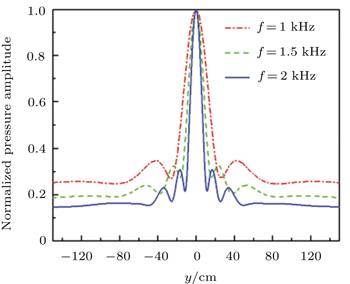
We have further calculated the transverse profiles of the pressure amplitude passing through the focal spot at x = 40 cm for the designed AMFE lens with different frequencies, as shown in Fig.
We have proposed a two-dimensional acoustic Maxwell’s fish-eye lens based on the space-coiling acoustic metamaterials. The gradually-varied refractive index is obtained by adjusting the structural parameters of the space-coiling acoustic units to design the lens. We further simplify the fabrication process of acoustic Maxwell’s fish-eye lens. The proposed lens has the capability to focus the acoustic wave irradiated from a point source at the surface of the lens on the diametrically opposite side of the lens. The broadband and low loss performance of the lens is further confirmed. The proposed acoustic fish-eye lens is expected to have the potential applications in directional acoustic coupler or coherent ultrasonic imaging.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 |