† Corresponding author. E-mail:
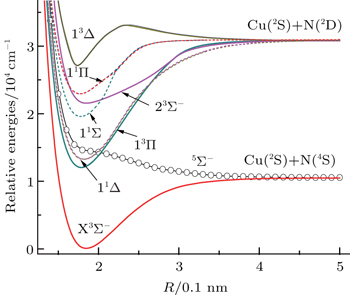
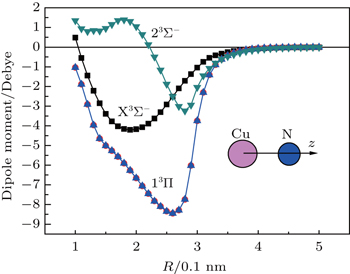
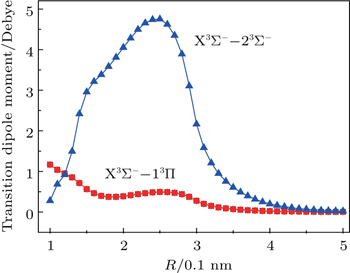
The high accuracy ab initio calculation method of multi-reference configuration interaction (MRCI) is used to compute the low-lying eight electronic states of CuN. The potential energy curves (PECs) of the X3Σ−, 13Π, 23Σ−, 13Δ, 11Δ, 11Σ−, 11Π, and 5Σ− in a range of R = 0.1 nm–0.5 nm are obtained and they are goodly asymptotes to the Cu(2Sg) + N(4Su) and Cu(2Sg) + N(2Du) dissociation limits. All the possible vibrational levels, rotational constants, and spectral constants for the six bound states of X3Σ−, 13Π, 23Σ−, 11Δ, 11Σ−, and 11Π are obtained by solving the radial Schrödinger equation of nuclear motion with the Le Roy provided Level8.0 program. Also the transition dipole moments from the ground state X3Σ− to the excited states 13Π and 23Σ− are calculated and the result indicates that the 23Σ−–X3Σ− transition has a much higher transition dipole moment than the 13Π–X3Σ− transition even though the 13Π state is much lower in energy than the 23Σ− state.
Transition metal compounds are very important in organometallic chemistry, surface science, astrophysics, catalysis process, and others.[1–3] The knowledge of the electronic states as well as the potential energy curves (PECs) are crucial information for experimental spectroscopic studies, and they are also important for depositing the nanoscale function material films.[4] But the compounds, even though the diatomic transition-metal mononitride, are electronically complex and very difficult to treat theoretically because of the extent of electron correlation. In experiments, almost no experimental studies for CuN were conducted until recently O’Brien et al.[5] produced the gas phase CuN molecules by using a copper hollow cathode in a plasma discharge. Through the intracavity laser absorption spectroscopy, they observed the electronic transition spectrum of CuN in the near infrared with red-degraded bandheads at 13005, 12963, 12957, and 12948 cm−1. They tentatively attributed these transitions to being due to the absorption from the X3Σ− ground state of CuN. But a strong perturbation was also observed in one of the excited states. Theoretically, there are several studies devoted to predicting the electronic structures of CuN and CuN+ species.[6–9] Ferrao et al.[6] studied the spectroscopic properties of the ground electronic state for CuN by the CCSD(T) approach and DFT (BP86, BPW91, B3LYP) methods through using the Wachters+f basis sets for the Cu atom and aug-cc-pVTZ basis set for the N atom, and the bond distances, harmonic vibrational frequencies, dissociation energies, ionization potentials, and electron affinity were obtained. Wu[7] also studied the electronic ground state of CuN (cation, neutral, and anion) species by various DFT methods (B3LYP, BLYP, BHLYP, BPW91, and B3PW91). Xu et al.[8] obtained the potential energy curve for the ground state of the CuN molecule by the density function theory (B3LYP) method where the effective core basis set of LANL2DZ for Cu atom and Pople’s basis set of 6-311+(d) for the N atom were used. Daoudi et al.[9] reported the electronic structure and bonding calculations for low-lying states of CuN and CuN+ with CIPSI (configuration interaction by perturbation of a multiconfiguration wave function selected iteratively) method, and indicated that the ground state of CuN is X3Σ− and the first low-lying excited state is 1Δ located at 1.45 eV.
However, the structure of the excited electronic states of CuN in the gas phase seems to be not well understood. In this paper, we focus on the eight low-lying electronic states of CuN, which are corresponding to the two dissociation limits Cu(2Sg) + N(4Su) and Cu(2Sg) + N(2Du), and the PECs of these states are obtained by using the multi-reference configuration interaction (MRCI) method where the Ahlrichstype basis set of def2-tzvp is selected for both Cu atom and N atom. The properties of PECs, vibrational levels, rotation constants, spectral constants, and transition dipole moments for the electronic states of CuN are discussed.
The MRCI method is considered to be one of the most reliable methods of studying electronic excited states due to the electron correlation energy to be fully considered in calculations. In this paper, the ORCA program package[10] is used for the PEC calculations as in our calculations of BeCl[11] and CuC.[12] The reference wave functions for the multireference calculations are of the state-averages complete active space self-consistent field (CASSCF) type.[13,14] The Ahlrichs triple-zeta valence with new polarization function basis set def2-TZVP[15] is used for both transition metal atom Cu and the ligand atom N, where the {17s11p7d1f} atomic orbitals of the Cu atom are contracted to {6s4p4d1f} pattern {842111/6311/4111/1}, and the {11s6p2d1f} orbitals of the N atom are contracted to {5s3p2d1f} pattern {62111/411/11/1}. The final total number of contracted basis functions is 76.
Our calculations focus on the low-lying electronic states which correspond to the dissociation limits Cu(2Sg) + N(4Su) and Cu(2Sg) + N(2Du), where the Cu keeps in the ground state 2Sg. The ratio of the expectation values of the 4s and 3d radii of Cu is 〈r4s〉/〈r3d〉 ≈ 3.4 at the Hartree–Fock numerical level,[16] and the Hartree–Fock energy levels of 3d and 4s orbital of Cu are (−13.32) eV and (−6.54) eV. Considering the dissociation limits of Cu(2Sg) + N(4Su) and Cu(2Sg) + N(2Du) to be little related to the 3d electron of Cu, it is appropriate to choose only the 4s1 electron of Cu and the 2s22p3 electrons of N as the active electrons and the corresponding orbitals of 4s(Cu), 4p(Cu), 2s(N), and 2p(N) as the active orbitals. So a 6-electron, 8-orbital complete active space multiconfiguration SCF calculation is performed, which is usually abbreviated as CAS(6,8).
The following MRCI calculation is performed by using the CAS(6,8) reference wave functions and estimating the higher-order excitations through the Davidson correction.[17] The excitation type is selected as CISD (single, double excitation configuration interaction), the threshold for the 0th order approximation to the target state is set to be Tsel = 10− 6 Hartree (1 Hartree = 2 Ry = 27.2114 eV), and the second threshold to the 0th order state is set to be Tpre = 10− 4, which is dimensionless and refers to the weight of a given initial reference space.
The scanning step for the PECs is 0.01 nm in a range from 0.10 nm to 0.50 nm. Based on the calculated PECs with the MRCI +Q method, the radial Schrödinger equation of nuclear motion is solved by using the Le Roy provided Level 8.0 program,[18] and the all possible vibrational energy levels are calculated and spectroscopic constants are obtained for each electronic bound state.
According to the diatomic molecular structure theory,[19] each electronic state of CuN is related to a specific dissociation limit of Cu + N. For the lowest dissociation limit Cu(2Sg) + N(4Su), only two molecular electronic states are derived in accordance with the Wigner–Witmer rules, where the atomic state 2Sg of Cu corresponds to 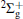
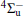
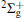
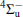

Figure
| Table 1. Some important parameters for the low-lying electronic states of CuN calculated with MRCI +Q method. . |
It is clear that the ground state is the X3Σ− state and the bond length is Re = 0.1836 nm with the lowest energy (−1693.83048) Hartree. We have set this energy to be the reference zero energy level in Fig.
Owing to the ground state of CuN being a triplet state, the allowed electronic transitions between the low-lying excited states and the X state are 23Σ− –X3Σ− and 13Π –X3Σ−. Using the MRCI method to calculate the PECs of CuN, the dipole moments with different bond distances for the X3Σ−, 13Π, and 23Σ− states are computed as shown in Fig.
As shown in Fig.
| Table 2. Main electron configurations for the X3Σ−, 13Π, and 23Σ− states at specific nuclear distances. . |
The variations of transition dipole moments of 23Σ−–X3Σ− and 13Π–X3Σ− with internuclear distance are also computed when scanning the PECs of CuN. As shown in Fig.
Based on the MRCI +Q calculated PECs as shown in Fig.
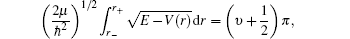
| Table 3. Partial vibrational levels and rotational constants (in unit cm− 1) of CuN for X3Σ−, 13Π, 23Σ−, 13Δ, 11Δ, 11Σ−, and 11Π states. . |
Substituting the calculated vibrational level energy into the G(υ) = ωe(υ + 1/2) − ωexe (υ +1/2)2 and the rotational constant into Bυ = Be − αe (υ + 1/2), through the least square fitting, the spectroscopic constants for these bound states are determined as shown in Table
| Table 4. Spectroscopic constants of the low-lying electronic states of CuN. . |
In the present study, we calculated the low-lying electronic states of CuN corresponding to the two dissociation limits Cu(2Sg) + N(4Su) and Cu(2Sg) + N(2Du) by making use of the multi-reference configuration interaction (including Davidson correction) method. The potential energy curves (PECs) of the X3Σ−, 13Π, 23Σ−, 3Δ, 11Δ, 11Σ−, 11Π, and 5Σ− in a range of R = 0.1 nm∼0.5 nm are obtained. Based on the potential energy curves, all the possible vibrational energy levels, rotational constants, and the corresponding spectroscopic constants for the bound states are obtained, meanwhile, the transition dipole moments from the ground state X3Σ− to the excited states 13Π and 23Σ− are calculated and the result indicates that the 23Σ−−X3Σ− transition keeps a higher transition dipole moment than the 13Π−X3Σ− transition at different nuclear distances.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 |