Cite this Article
Ali M A, Nasir M T, Khatun M R, Islam A K M A, Naqib S H. An ab initio investigation of vibrational, thermodynamic, and optical properties of Sc2AlC MAX compound. Chinese Physics B, 2016, 25(10): 103102  
Permissions
An ab initio investigation of vibrational, thermodynamic, and optical properties of Sc2AlC MAX compound
Ali M A1, Nasir M T4, Khatun M R2, Islam A K M A3, Naqib S H2, †,
Department of Physics, Chittagong University of Engineering and Technology, Chittagong-4349, Bangladesh
Department of Physics, University of Rajshahi, Rajshahi-6205, Bangladesh
International Islamic University Chittagong, 154/A College Road, Chittagong, Bangladesh
Department of Arts & Sciences, Bangladesh Army University of Science and Technology, Saidpur-5310, Nilphamari, Bangladesh

 

† Corresponding author. E-mail: salehnaqib@yahoo.com

Abstract
Abstract

The structural vibrational, thermodynamical, and optical properties of potentially technologically important, weakly coupled MAX compound, Sc2AlC are calculated using density functional theory (DFT). The structural properties of Sc2AlC are compared with the results reported earlier. The vibrational, thermodynamical, and optical properties are theoretically estimated for the first time. The phonon dispersion curve is calculated and the dynamical stability of this compound is investigated. The optical and acoustic modes are observed clearly. We calculate the Helmholtz free energy (F), internal energy (E), entropy (S), and specific heat capacity (Cv) from the phonon density of states. Various optical parameters are also calculated. The reflectance spectrum shows that this compound has the potential to be used as an efficient solar reflector.

PACS: 31.15.A–;63.20.D–;65.40.–b;78.20.Ci
Keyword:MAX compound;phonon dispersion;thermodynamical properties;optical properties
1. Introduction

Sc2AlC belongs to the prototype of a vast family of ternary nitrides and carbides widely known as MAX compounds.[1] These materials represent a class of condensed phases that can be regarded as thermodynamically stable nanolaminates. MAX phases have attracted significant attention from the scientific community because of their striking combination of properties, some of which are like those of ceramics and others are like metals.[2]

To be specific, these compounds like industrially important metals with low density possess machinability, damage tolarence, thermal, and electrical conductivity. On the other hand, they possess high elastic stiffness, refractory nature and are resistant to high-temperature oxidation just as engineering ceramics.[3] All these attributes make MAX phases attractive for high performance applications in diverse fields from defense materials to electronic devices. So far, over 70 different MAX phases have been experimentally synthesized.[4] Many more MAX phases have been predicted and are being explored both experimentally and theoretically at present. Sc2AlC is one of those. The M2AX phases with M = Ti, V, Cr, Nb, Ta, Zr, Hf; A = Al, S, Sn, As, In, Ga, and X = N, C, have been studied extensively both experimentally and theoretically.[4] Nevertheless, the Sc2AlC phase remains one of the least studied materials in the 211 MAX family.

A few first-principles calculations of the Sc2AlC phase can be found in the literature. The structural and elastic properties have been addressed by Bouhemadou et al.[5] Cover et al.[6] also studied the elastic properties of this compound. Electronic properties have been studied by Music et al.[7] Though elastic and electronic properties have been studied, the lattice dynamical (vibrational), thermodynamic, and optical properties have not been theoretically explored so far for this compound. This paper attempts to bridge this gap through DFT based ab-initio calculations.

The thermodynamic properties of a compound are extremely important in solid state science and are considered as key factors in designing functional materials to be used under high temperature and high pressure conditions. Optical parameters, on the other hand, provide the information about the electronic response of the material subjected to incident electromagnetic radiation. Optical properties are intimately related to the electronic band structure and topology of the incipient Fermi surface.[8] Therefore, investigations of these properties are desirable both from the point of view of fundamental physics and from the potential large scale industrial applications.

In the present work, we aim to add novel theoretical results to the results of the existing literature on the physical properties of possible Sc2AlC phase by using the first-principles method. We especially focus on the vibrational, thermodynamic, and optical properties. The rest of the paper is organized as follows. Section 2 describes the computational procedure in brief. Theoretical results of analysis are presented and discussed in detail in Section 3. Major conclusions are drawn from the theoretical findings in Section 4.

2. Computational method

The CASTEP (Cambridge serial total energy package) code[9] is used to calculate the structural, vibrational, thermodynamic and optical properties of Sc2AlC. In ab-initio calculations, we use the plane wave pseudopotential approach based on the density functional theory (DFT).[10] The crystal parameters are obtained via geometry optimization which is performed through minimizing the total energy and internal forces by using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) minimization technique.[9] During computations, the exchange–correlation is treated within the GGA (generalized gradient approximation) PBE (Perdew–Burke–Ernzerhof) functional.[11] To sample the first Brillouin zone, a k-point grid of 9 × 9 × 2 mesh according to the Monkhorst–Pack scheme[12] is employed for all calculations with a spacing of 0.02 Å−1. The convergence of the planewave expansion is acquired with a kinetic energy cutoff of 500 eV. Excellent convergence is guaranteed by testing the Brillouin zone sampling and the kinetic energy cutoff which employs the tolerance for self-consistent field, energy, maximum force, maximum displacement, and maximum stress as 5.0 × 10−7 eV/atom, 5.0 × 10−6 eV/atom, 0.01 eV/Å, 5.0 × 10−4 Å, and 0.02 GPa, respectively. Phonon dispersion is obtained using the DFPT linear-response method.[13] Quasi-harmonic approximation is used to obtain the thermodynamic properties from the phonon dispersion curve and phonon density of states.

3. Results and discussion
3.1. Structural properties

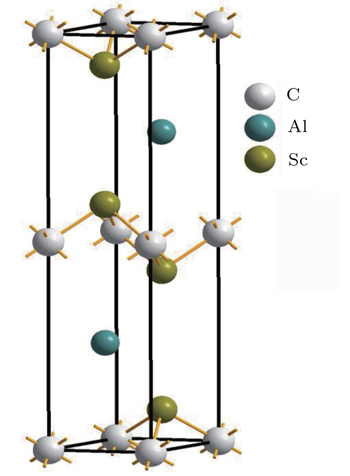
From previous studies[5–7] the Sc2AlC compound is expected to crystallize under ambient conditions in the Cr2AlC crystal structure, with space group P63/mmc (No. 194). The compound has eight atoms in each unit cell and the unit cell contains two formula units. The positions of atoms in Sc2AlC are as follows: C atoms are placed at the positions (0,0,0), the Al atoms are at (1/3,2/3,3/4), and the Sc atoms are at (1/3,2/3,zM).[14] The lattice parameters a,c, and zM are used to determine the crystal structure, where a and c are the lattice constants and zM is the internal structural parameter. The optimized unit cell is shown in Fig. 1. The optimized values of structural parameters of Sc2AlC are given in Table 1. Our results are in good agreement with the theoretical results in Refs. [5] and [7].

Fig. 1. Unit cell of Sc2AlC MAX nanolaminate.
Table 1.

Optimized lattice parameters (a and c, in unit Å), hexagonal ratio c/a, internal parameter zM, unit cell volume V (in unit Å3) for MAX phases Sc2AlC.

.
3.2. Vibrational properties

Figure 2 presents the ground state (ambient) phonon dispersion curves and phonon density of states (PHDOS) along the high-symmetry directions of the crystal Brillouin zone. There are neither experimental nor theoretical data available at this moment; therefore, a comparison is not possible at this time. The corresponding frequencies for longitudinal optical (LO) and transverse optical (TO) modes at the zone centre are 17.3 THz and 12.2 THz, respectively.

Fig. 2. (a) Phonon dispersion curves and (b) phonon density of states of Sc2AlC.

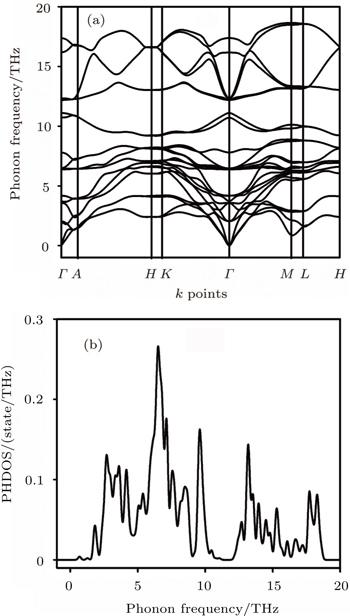
The highest point for LO is not located at zone center but at the high symmetry point of M.

The separation between LO and TO in the zone center is 5.2 THz. A compound is considered to be dynamically stable if the phonon frequencies for all the wave vectors are positive. A compound, on the other hand, is treated as dynamically unstable, if there is any imaginary phonon frequency at any wave vector. Since, in our present case all the frequencies are positive, therefore the phase under consideration is dynamically stable. At this point it should be mentioned that Music et al.[7] calculated the formation enthalpies of Sc2AC (A = Al, Ga, In, Tl) MAX phases and found them to be chemically stable. Besides, Bouhemadou et al.[5] and Cover et al.[6] showed that the calculated elastic constants of Sc2AlC satisfy the Born criteria[15] for mechanical stability. Figure 2(a) also depicts that there is a clear gap between acoustic branch and optical branch in the whole BZ as indicated by the phonon dispersion curves and PHDOS in Fig. 2(b).

3.3. Thermodynamic properties

A complete description of a system equilibrium behavior is contained in its thermodynamic potentials. We obtain these thermodynamical potential functions such as Helmholtz free energy F, internal energy E, entropy S, and specific heat Cv of Sc2AlC at zero pressure by using the calculated phonon density of states through employing the quasi-harmonic approximation.[16] The following equations are used to calculate the F, E, S, and Cv:[17]

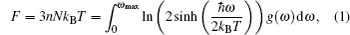
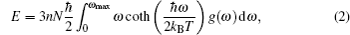
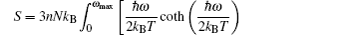
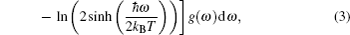
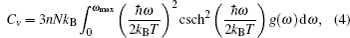
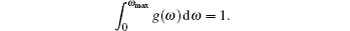
where kB is the Boltzmann constant, n is the number of atoms per unit cell, N is the Avogadro number, ωmax is the cut-off phonon frequency, ω is the phonon frequency, and g(ω) is the normalized phonon density of states, with

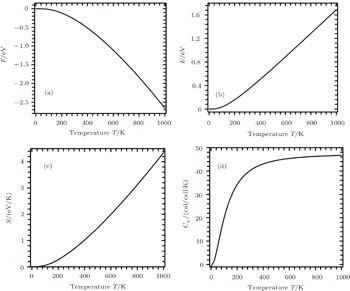The calculated results of F, E, S, and Cv are shown in Figs. 3(a)–3(d) in a temperature range from 0 K to 1000 K. Helmholtz free energy (F) of Sc2AlC is displayed in Fig. 3(a), in which the free energy gradually decreases with increasing temperature. The decreasing trend of free energy is very common and it becomes more negative during the course of any natural process. The degree of decrease in free energy is determined by the entropy (S) of any system. The entropy of a system increases with increasing temperature since thermal agitation adds to disorder. This is shown in Fig. 3(c). Contrary to the free energy, the internal energy (E) shows an increasing trend with temperature rising as shown in Fig. 3(b).

Fig. 3. Temperature dependences of the calculated thermodynamic parameters of Sc2AlC under zero pressure: (a) Helmholtz free energy, (b) internal energy, (c) entropy, and (d) specific heat.

The behaviors of materials under different thermodynamical constraints can be explained in terms of the specific heat of a solid. It also determines how efficiently the material stores heat. The phonon contribution dominates Cv as a function of temperature. Figure 3(d) shows that the specific heat Cv of Sc2AlC follows the Debye model which is proportional to T3, as expected.[18] This model correctly predicts the temperature dependence of the heat capacity at constant volume and low temperature. It is seen that the heat capacity of Sc2AlC increases rapidly with temperature rising up to 300 K. It is also found that the Dulong–Petit law is recovered at high temperatures.[19]

In an ordinary metallic system, the total specific heat is composed of two components: one is due to the phonons and the other is due to the mobile charge carriers (electrons, for Sc2AlC). From the published value of the electronic energy density of states at the Fermi level, N(ɛF), for Sc2AlC,[7] we calculate the coefficient of electronic specific heat, γe, given by

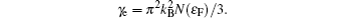
We obtain γe = 1.61 mcal/mole·K2. This yields an electronic specific heat of 1.61 cal/mole·K at 1000 K. This is less than 7% of the phonon specific heat at the same temperature, indicating that for the temperature range of practical interest, the specific heat of Sc2AlC is almost completely dominated by the phonon contribution.

The Debye temperature, θD, is an important parameter related to many thermophysical properties. In general, a high Debye temperature implies strong bonding among the atoms and a higher phonon contribution to thermal conductivity. The estimated θD from the phonon spectrum is around 638 K. θD can also be calculated from various elastic constants. Following the procedure reported in Ref. [20], we also calculate θD from elastic constants, which is 558 K.

3.4. Optical properties

When an electromagnetic radiation is incident on the materials, different materials behave in different ways. The optical constants determine the overall response of the sample to the incident radiation. The complex dielectric function, defined as ɛ(ω) = ɛ1(ω) + iɛ2(ω), is one of the main optical characteristics of a solid. The other optical constants can be extracted from this complex function. The imaginary part ɛ2(ω) is calculated by CASTEP[21] numerically through directly evaluating the transition matrix elements between the occupied and unoccupied electronic states. The expression for the ɛ2(ω) can be found elsewhere.[22,23] The Kramers–Kronig (KK) relations are used to derive the real part ɛ1(ω) of a dielectric function from the calculated imaginary part. The other optical constants described in this section are derived from ɛ1(ω) and ɛ2(ω) by using the equations given in Ref. [21]. Information regarding optical constants is important in display technology.

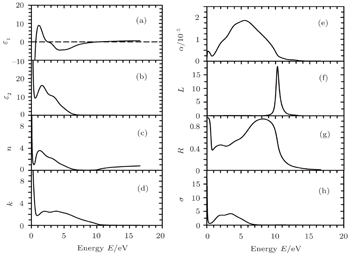
The optical parameters and optical conductivity of Sc2AlC are shown in Fig. 4 (left and right panels) for the (100) polarization direction of the incident electric field. To smear out the Fermi level for effective k-points on the Fermi surface, we have used a 0.5-eV Gaussian smearing. A Drude term with an unscreened plasma energy of 3 eV and a damping term of width 0.05 eV have also been used.

Fig. 4. Energy dependences of the calculated optical parameters of Sc2AlC: (a) real part of dielectric constant, (b) imaginary part of the dielectric constant, (c) refractive index, (d) extinction coefficient, (e) absoption coefficient, (f) loss function, (g) reflectance, and (h) optical conductivity.

Optical parameters give a useful insight into the underlying electronic band structure. The electronic properties of crystalline material are mainly characterized by the imaginary part, ɛ2(ω) of dielectric function ɛ(ω) which is related to the photon absorption phenomenon. The peaks in ɛ2(ω) are associated with electron excitations. For the compound under study, there is only one prominent peak at 2.85 eV (Fig. 4(b)). The large negative value of ɛ1 is also observed in Fig. 4(a), which is a clear indication of the Drude-like behavior seen in metal. The refractive index, n, is another technically important parameter for optoelectronic materials. The frequency-dependent refractive index is shown in Fig. 4(c). The extinction coeffient k is exhibited in Fig. 4(d). The extinction coefficient measures the degree of attenuation of electromagnetic radiation inside the solid.

Figure 4(e) shows the behavior of the absorption coefficient spectrum of Sc2AlC. This reveals the metallic nature of the compound since the absorption coefficient is finite at zero energy. There is no discernible band gap, and the free carrier absorption dominates at low energies.

The loss function L(ω), is shown in Fig. 4(f). The loss function measures the energy loss of an electron with high velocity passing through the material. This curve features a peak at an energy which gives the bulk plasma frequency ωp, that occurs at the onset of ɛ2 < 1 and ɛ1 = 0.

From Fig. 4(f), the value of the effective plasma frequency ωp can be found to be ∼ 10.3 eV. A metal becomes transparent, when the frequency of incident photons is greater than ωp. The reflectivity curve is shown in Fig. 4(g). It is seen that the reflectance curve starts with a high value of ∼ 0.90–0.98, decreases and then rises again to reach the maximum value in a range of ∼ 0.80–0.90 between 6 eV and 10 eV. The large reflectivity at very low energies indicates that the dynamical conductivity is quite high for Sc2AlC in the low energy (frequency) region. Moreover, the peak of loss function is associated with the trailing edge of the reflection spectrum as expected theoretically.

Since the material under study has no band gap, the photoconductivity starts (with a high value) at zero photon energy as shown in Fig. 4(h) confirming the fact that Sc2AlC is metallic in nature.

4. Conclusions

The vibrational, thermodynamic and optical properties of the Sc2AlC MAX compound are investigated for the first time by the DFT-based first-principles method. Structural properties are compared and found to be in good agreement with available results. The phonon dispersion curve indicates that Sc2AlC is dynamically stable. This supports the earlier studies in which it was indicated that the predicted Sc2AlC MAX nanolaminate is mechanically and chemically stable.[5–7] Clear separation between acoustic and optical branches is seen. Thermodynamic properties are obtained from phonon density of states. The Debye temperature is relatively high. A high Debye temperature usually implies a high phonon thermal conductivity. The optical parameters, such as the real and imaginary parts of the dynamical susceptibility, absorption coefficient, loss function, and photoconductivity spectrum reveal the metallic nature of Sc2AlC. The low energy optical conductivity is quite high. The reflectance spectrum of the compound under study shows that it might be used as a shielding material to avoid solar heating. We hope that the experimentalists will be encouraged to use the findings of this study to explore this material in greater detail in the near future.

Reference
1Nowotny H1970Progress Solid State Chemistry 2, ed. Reiss HNew YorkPergamon Press
2Barsoum M W 2000 Prog. Solid State Chem. 28 201
3Finkel PBarsoum M WEl-Raghy T 2000 J. Appl. Phys. 87 1701
4Wang JZhou Y 2009 Ann. Rev. Mater. Res. 39 415
5Bouhemadou AKhenata RKharoubi MMedkour Y 2008 Solid State Commun. 146 175
6Cover M FWarschkow OBilek M M MMcKenzie D R 2009 J. Phys.: Condens. Matter 21 305403
7Music DSun ZScheider J M 2005 Solid State Commun. 133 381
8Du Y LSun Z MHashimoto HTian W B 2009 Mater. Trans. 50 2173
9Segall M DLindan P J DProbert M JPickard C JHasnip P JClark S JPayne M C 2002 J. Phys.: Condens. Matter 14 2717
10Payne M CTeter M PAllan D CArias T AJoannopoulos J D1992Rev. Mod. Phys.651045
11Perdew J PErnzerof K 1996 Phys. Rev. Lett. 77 3865
12Monkhorst H JPack J 1976 Phys. Rev. 13 5188
13Refson KClark S JTulip P R 2006 Phys. Rev. 73 155114
14Yakoubi ABeldi LBouhafs BFerhat MRuterana P 2006 Solid State Commun. 139 485
15Born M 1940 Math. Proc. Camb. Philos. Soc. 36 160
16Isaev E Ihttps://qe-forge.org
17Lee CGonze X 1995 Phys. Rev. 51 8610
18Debye P1912Ann. Phys.39789
19Petit A TDulong P L1981Ann. Chem. Phys.10395
20Hadi M AAlam M ARoknuzzaman MNasir M TIslam A K M ANaqib S H 2015 Chin. Phys. 24 117401
21Materials Studio CASTEP Manual & Accelrys 2010, http://www.tcm.phy.cam.ac.uk/castep/documentation/WebHelp/CASTEP.htmlS
22Ali M AIslam A K M AAli M S2012J. Sci. Res.41
23Ali M AJahan NIslam A K M A2014J. Sci. Res.6407