† Corresponding author. E-mail:
Project supported by the National Basic Research Program of China (Grant No. 2012CB821305) and the National Natural Science Foundation of China (Grant Nos. 11474319, 11274348, and 91536102).
The B-spline configuration-interaction method is applied to the investigations of dynamic dipole polarizabilities for the four lowest triplet states (2 3S, 33S, 23P, and 33P) of the Li+ ion. The accurate energies for the triplet states of n3S, n3P, and n3D, the dipole oscillator strengths for 23S(33S) → n3P, 23P(33P) → n3S, and 23P(33P) → n3D transitions, with the main quantum number n up to 10 are tabulated for references. The dynamic dipole polarizabilities for the four triplet states under a wide range of photon energy are also listed, which provide input data for analyzing the Stark shift of the Li+ ion. Furthermore, the tune-out wavelengths in the range from 100 nm to 1.2 μm for the four triplet states, and the magic wavelengths in the range from 100 nm to 600 nm for the 23S → 33S, 23S → 23P, and 23S → 33P transitions are determined accurately for the experimental design of the Li+ ion.
Since the relativistic and QED corrections in the Li+ ion should be larger than in helium due to the Z4 scaling of the energy, the studies of the Li+ ion are of great interest because of its wide applications. For example, the combination between the experimental measurements and the theoretical calculations of the 23S hyperfine splitting for the Li+ ion provides a sensitive test of the hyperfine atomic structure theory,[1–3] and the investigation of the 23PJ fine structure of the Li+ ion can be used to determine the fine structure constant.[4–8] In addition, the high-precision measurement of the 23S → 23P transition for the Li+ ion isotopes could be used to test the relativistic and QED corrections,[2,3,9] to extract the relative nuclear charge radius,[10] to test the time dilation and verify the special relativity.[11]
The dynamic dipole polarizabilities of ions, which describe the distortion of the electronic charge distribution in the presence of an oscillating electric field with angular frequency ω, play an important role in the calculations of the van der Waals C6 coefficient,[12,13] in the determinations of refractive index and dielectric constants of ionic crystals,[14] in the construction of a core-polarization model for atoms and molecules,[15,16] and in the analysis of the Stark shifts.[17–19] Especially, the tune-out and magic wavelengths,[18,20,21] which are extracted from the dynamic dipole polarizabilities, become important parameters for experimental design of ion trapping. For example, recently, Liu et al. suggested that the magic wavelengths of ions pave a way to build an all-optical trapped ion[17,22–24] to eliminate the second-order of Ac Stark shift.
At present, there many works reporting the calculation of the static dipole polarizability of the ground-state Li+ ion.[25–31] For example, Zhu et al. computed the nonrelativisitc polarizabilities by using Hylleraas basis,[29] Johnson and Cheng got the polarizability by exploiting the B-spline relativistic configuration interaction (CI) method to solve the Dirac–Coulomb–Breit equation,[30] and Lim et al. obtained the polarizability by using the fully relativistic coupled-cluster method.[32] For the dynamic polarizabilities of the Li+ ion, Chung applied the variational perturbation method into the calculation of the ground state dynamic dipole polarizabilities,[33] and Glover and Weinhold obtained the rigorous upper and lower bounds for dynamic dipole polarizabilities with the laser frequency up to the first excitation threshold of the ground state.[25] However, compared with the ground-state polarizabilities, there are several calculations of polarizabilities for the triplet states of the Li+ ion. For example, the static dipole polarizability for the 23S and 23P states can be found in Refs. [34]–[36], only two works[37,38] about the dynamic polarizabilities for the 23S state were published, and there has been no work reported for the dynamic dipole polarizabilities of other triplet states of the Li+ ion in the literature.
In the present study, the CI method based on B-spline functions developed in our previous work[39] is extended to calculate the dynamic dipole polarizabilities for the four lowest triplet states of the Li+ ion. The tune-out wavelengths for the 23S, 23P, 33S, and 33P states are determined, and the magic wavelengths for the 23S → 33S, 23S → 23P, and 23S → 33P transitions are tabulated for reference. Atomic units are used throughout this paper unless specifically mentioned.
Taking the Li+ ion as a Coulomb three-body system, choosing the atomic nucleus as particle 0 and two electrons as particle 1 and particle 2, respectively, the Hamiltonian can be written as
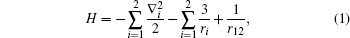
Recently, significant progress has been made in the variational calculations for two-electron systems by using the B-spline CI basis set,[39–42] which has the following functional form,
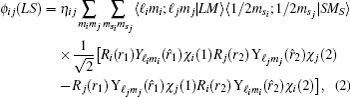
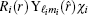
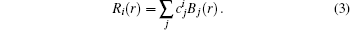
Using the variational method, the expectation value of the Hamiltonian can be simplified to the following configuration equation,
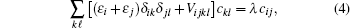
The present CI calculation is performed by fixing the box size R0 = 150 a.u. (the unit a.u. is short for atomic unit), the nonlinear parameter γ = R0 × 0.042, and the order of the B-spline k = 7. The convergence test of the energies and oscillator strengths are performed as the number of B-spline N and partial waves ℓmax increased. The maximum N and ℓmax used in our calculation are respectively 40 and 10.
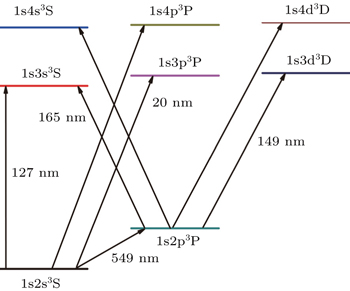
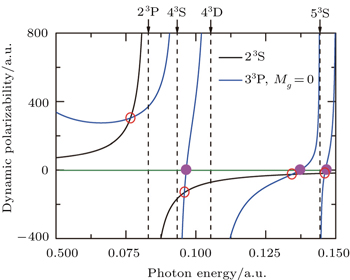
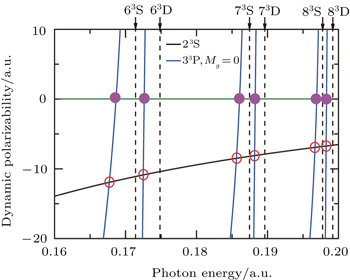
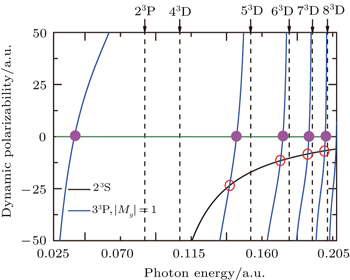
Figure
Table
| Table 1. Comparison of the energies (in unit a.u.) for the Li+ ion. The experimental data were taken from the National Institute of Science and Technology (NIST) tabulation.[43] The numbers in the parentheses are the computational uncertainties. . |
The extrapolated oscillator strengths for some selective dipole transitions are presented in Table
| Table 2. Comparison of the oscillator strengths for the Li+ ion. The numbers in the parentheses represent computational uncertainties. . |
When an atom or ion is exposed at the external electric field with the photon energy of ω, the dynamic dipole polarizabilities for the magnetic sub-level |NgLgMg〉 with the main quantum number Ng, angular momentum quantum number Lg, and magnetic quantum number Mg, can be expressed as
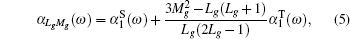
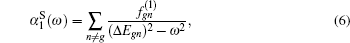
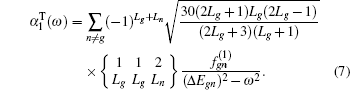




| Table 3. Convergence of the static dipole polarizabilities (in unit a.u.) for the 23S state of the Li+ ion as the number of B-spline N and partial waves ℓmax increased. The number in parenthesis for the extrapolated value gives the computational uncertainty. . |
| Table 4. Dynamic dipole polarizabilities (in unit a.u.) of the 23S, 23P, 33S, and 33P states for the Li+ ion. The numbers in parentheses represent computational uncertainties. . |
The dynamic dipole polarizabilities for the 23S state of the Li+ ion for some selective photon energy of 0 ≤ ω ≤ 0.38 a.u. are listed in Table 
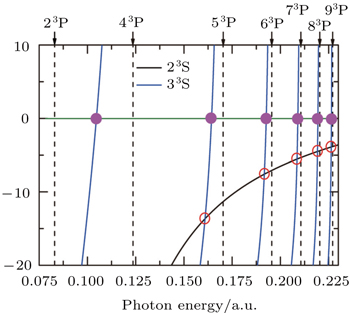
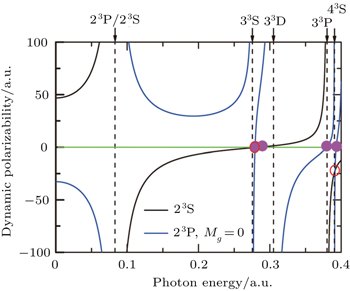
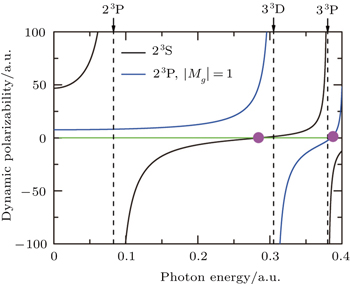
The tune-out wavelength is defined as the wavelength which makes the dynamic dipole polarizability of a single state disappear.[49,50] The magic wavelength is defined as the wavelength which makes the dynamic dipole polarizabilities of the upper and lower energy levels of a transition equal.[51–53] The dynamic dipole polarizabilities for the lowest four triplet states of the Li+ ion are also plotted in Figs.
The values of the tune-out and magic wavelengths in the Figs.
| Table 5. Tune-out wavelengths λt (in unit nm) for 23S, 33S, 23P, and 33P states of the Li+ ion. The numbers in parentheses give the computational uncertainties. . |
| Table 6. Magic wavelengths λm (in unit nm) for 23S → 33S, 23S → 23P, and 23S → 33P transitions of the Li+ ion. The numbers in parentheses give the computational uncertainties. . |
The ab-initio calculations of the dynamic dipole polarizabilities for the four lowest triplet states (2 3S, 33S, 23P, and 33P) of the Li+ ion are carried out by using the B-spline CI method. The large number of accurate energies and oscillator strengths with the main quantum number n up to 10 of the Li+ ion are tabulated for theoretical references. Present static dipole polarizabilities for the 23S and 23P states are in excellent agreement with the most accurate results from variational Hylleraas basis calculations,[35,36] and present dynamic dipole polarizabilities for the 23S state that lies within the upper and lower bounds of the values from the correlated variational trial function calculation.[37] In addition, the tune-out wavelengths for the four lowest triplet states, and the magic wavelengths for the three transitions of 23S → 33S, 23S → 23P, and 23S → 33P are identified with at least four significant digits. Present polarizabilities provide theoretical references for analyzing the Stark shift of the Li+ ion. Our tune-out and magic wavelengths can be used for designing the high-precision experimental measurement on the Li+ ion in the future.
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 | |
| 26 | |
| 27 | |
| 28 | |
| 29 | |
| 30 | |
| 31 | |
| 32 | |
| 33 | |
| 34 | |
| 35 | |
| 36 | |
| 37 | |
| 38 | |
| 39 | |
| 40 | |
| 41 | |
| 42 | |
| 43 | |
| 44 | |
| 45 | |
| 46 | |
| 47 | |
| 48 | |
| 49 | |
| 50 | |
| 51 | |
| 52 | |
| 53 |