Cite this Article
Lin Cheng-You, Yin Liang, Chen Shu-Jing, Chen Zhao-Yang, Ding Ying-Chun. Effects of dispersion and filtering induced by periodic multilayer mirrors reflection on attosecond pulses. Chinese Physics B, 2016, 25(9): 097802  
Permissions
Effects of dispersion and filtering induced by periodic multilayer mirrors reflection on attosecond pulses
Lin Cheng-You1, †, , Yin Liang1, Chen Shu-Jing2, Chen Zhao-Yang1, Ding Ying-Chun
College of Science, Beijing University of Chemical Technology, Beijing 100029, China
Beijing Key Laboratory of Materials Utilization of Nonmetallic Minerals and Solid Wastes, National Laboratory of Mineral Materials, School of Materials Science and Technology, China University of Geosciences, Beijing 100083, China

 

† Corresponding author. E-mail: cylin@mail.buct.edu.cn

Project supported by the National Natural Science Foundation of China (Grant Nos. 11547183 and 11547241) and the Fundamental Research Funds for Central Universities, China (Grant Nos. JD1517 and 2652014012).

Abstract
Abstract

Using temporal and spectral methods, the effects of dispersion and filtering induced by Mo/Si multilayer mirrors reflection on incident attosecond pulses were studied. First, two temporal parameters, the pulse broadening factor, and the energy loss factor, were defined to evaluate the effects of dispersion and filtering. Then, by analyzing these temporal parameters, we investigated and compared the dispersion and filtering effects on attosecond pulses. In addition, we explored the origins of pulse broadening and energy loss by analyzing the spectral and temporal characteristics of periodic Mo/Si multilayer mirrors. The results indicate that the filtering effect induced by Mo/Si multilayer mirrors reflection is the dominant reason for pulse broadening and energy loss.

PACS: 78.67.Pt;41.50.+h;42.65.Re
Keyword:extreme ultraviolet region;multilayer mirrors;attosecond pulse;pulse broadening
1. Introduction

With the rapid progress of attosecond science in recent years,[1–3] multilayer mirrors in the extreme ultraviolet (EUV) and x-ray region for high-efficiency spectral and temporal control of attosecond pulses have attracted a great deal of interest.[4] As an efficient filter and reflector for attosecond sources, e.g., high-order harmonics (HOH),[5–8] the periodic Mo/Si multilayer mirror has been widely used in attosecond science for years.

In 2001, Dresher et al.[9] used a Mo/Si spherical periodic multilayer mirror with a 5-eV band centered at 90 eV to filter and focus EUV pulses. In 2002, Kienberger et al.[10] employed a high-reflectance Mo/Si multilayer mirror with a 15-eV band centered at 93 eV to select radiation for the photoionization experiments. In 2009, Abel et al.[11] made use of a Mo/Si multilayer mirror with a 4-eV band centered at 93 eV in the CEP-scanning experiments. In 2013, Zhan et al.[12] used a Mo/Si mirror for an isolated attosecond pulse reflection.

When using a multilayer mirror to reflect an attosecond pulse, the preservations of pulse duration and photon flux are usually the paramount requirements.[13] However, these requirements are hard to meet for a periodic multilayer mirror, due to its dispersion and filtering effects on the incident attosecond pulse, which can lead to pulse broadening and pulse energy loss. Although temporal pulse responses of periodic Mo/Si multilayer mirrors have been studied for years,[14–18] the effects of dispersion and filtering induced by Mo/Si multilayer mirrors reflection on attosecond pulses have not been investigated so far.

In this paper, we numerically studied the dispersion and filtering effects induced by Mo/Si multilayer mirrors reflection on attosecond pulses. First, two temporal parameters were defined to evaluate pulse broadening and energy loss of incident attosecond pulses quantitatively. Then, the effects of dispersion and filtering on attosecond pulses were investigated respectively. Finally, we compared the dispersion and filtering effects by analyzing the ratios of the pulse broadening factor and the energy loss factor of two effects. Research into the effects of dispersion and filtering induced by periodic Mo/Si multilayer mirrors reflection on attosecond pulses can improve the understanding of the origins of pulse broadening and pulse energy loss induced by periodic multilayer mirrors reflection, and provide a guide for attosecond multilayer mirrors design.

2. Theoretical methods
2.1. Model schematic

In Fig. 1, the schematic of an isolated attosecond pulse reflected by a periodic Mo/Si multilayer mirror is given. Here, θ is the incident angle of attosecond pulse, and only the normal incidence (θ = 0) case is considered in this paper, N is the bi-layer number of the multilayer mirror, ñ0, ñ1, ñ2, and ñs are the optical constants of air, Si, Mo, and the substrate, respectively, d1 and d2 are the thicknesses of Si and Mo layers, respectively. The period d(d = d1 + d2) and the thickness ratio γ = d2/(d1 + d2) were set to be 8.8 nm and 0.5 respectively, in order to make the Bragg reflection peaks of multilayer mirrors locate at 80 eV, in accordance with the central photon energies of incident attosecond pulses.

Fig. 1. The schematic diagram of an isolated attosecond pulse reflected by a periodic Mo/Si multilayer mirror.
2.2. Calculation method in frequency domain

To analyze the effects of dispersion and filtering induced by Mo/Si multilayer mirrors reflection on incident attosecond pulses in the frequency domain, the spectral complex amplitude reflection coefficient r(ω) = |r(ω)|exp[iϕ(ω)], which is the main parameter describing reflective performances of a multilayer mirror, needs to be determined firstly by using a standard matrix method based on the Fresnel equations as follows:[19]

where M is the characteristic matrix of the multilayer, and its matrix elements are A, B, C, and D, δj = 2πnjdjcosθj/λ, ηj = njcosθj (for s-polarization) or ηj = nj/cosθj (for p-polarization), nj and dj denote the optical constant and the thickness of each layer in the multilayer structure, and θj represents the refraction angle in each layer.

Using r(ω), we can calculate the spectral reflectivity R and the reflective phase ϕ(ω) of a multilayer mirror by

where Re(r(ω)) and Im(r(ω)) represent the real and the imaginary parts of r(ω) respectively.

In addition, the group delay dispersion GDD of a multilayer mirror, which plays an important role in the pulse broadening, can be obtained by

The optical constants of Mo and Si used in the simulation were derived from the handbook edited by Henke et al.[20] To provide a reasonable prediction of the performances of a multilayer mirror, the inter-diffusion effect between Mo and Si layers in the multilayer was considered in all cases, following a proven model used in the realistic design of Mo/Si multilayers.[21]

2.3. Calculation method in time domain

To determine the effects of dispersion and filtering on an incident pulse in the time domain, a typical temporal method based on Fourier transform, which has been used in temporal analysis of the performances of multilayer mirrors by Ksenzov et al.,[22,23] Wonisch et al.,[24] and Suman et al.[25] previously, was employed in our simulation.

First, we need to obtain the spectral component E0(ω) of an incident pulse from its temporal component E0(t) by Fourier transform. Then, to obtain the spectral component of the reflected pulse E1(ω), simply multiply E0(ω) with |r(ω)|(or exp [iϕ(ω)]), which describes the filtering (or dispersion) effects induced by a multilayer mirror reflection, finally, inverse Fourier transform with the object of E1(ω) to obtain the temporal component E1(t) and intensity I1(t) of the reflected pulse. The whole calculation procedure can be expressed by the following equations:

In addition, to describe the temporal effects of dispersion and filtering on incident attosecond pulses quantitatively, two temporal parameters were induced. The first one is the pulse broadening factor PBF, which describes the pulse broadening induced by a multilayer mirror reflection, and can be defined as the reflected-to-incident pulse duration ratio by

where τ0 and τ1 are the pulse durations of the incident and reflected attosecond pulses respectively, and τi (i = 0, 1) can be calculated by

where is the temporal intensity, and is the peak intensity of the incident (i = 0) or reflected pulses (i = 1). The second parameter is the energy loss factor ELF, which evaluates the energy loss of a pulse reflected by a multilayer mirror, can be defined as the decreased-to-original peak intensity ratio by

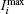
Furthermore, all incident isolated attosecond pulses used in our simulation were assumed to be non-chirped Gaussian-shaped pulses, and their temporal component E0(t) can be expressed by

where ω0 is the central frequency of incident pulse. In all cases, we set ω0 = 121.5 fs−1 to make central photon energies of incident attosecond pulses locate at 80 eV.

3. Results and discussion
3.1. The effect of dispersion on attosecond pulses

First, we studied the dispersion effect of periodic Mo/Si multilayer mirrors with different bi-layers (N = 1–50) on incident attosecond pulses with various durations (τ0 = 100 as, 200 as, 300 as, 400 as, 500 as (1 as = 10−18 s)) by calculating the pulse broadening factor PBFd and the energy loss factor ELFd (see Fig. 2).

Fig. 2. (a) The pulse broadening factor PBFd and (b) the energy loss factor ELFd describing the dispersion effect of periodic Mo/Si multilayer mirrors with N = 1–50 on incident attosecond pulses with τ0 = 100 as, 200 as, 300 as, 400 as, and 500 as.

For each incident attosecond pulse, both PBFd and ELFd increase rapidly until reaching their maximums, then decrease slowly with the increase of N. The maximums of PBFd and ELFd show at the same N (named Nmax), and Nmax for each case are listed in Table 1. The same trends of PBFd and ELFd with the increase of N indicate a proportional relation between the pulse broadening and the energy loss caused by the dispersion effect. To explore the reasons for the varied trends of PBFd and ELFd with changing N in detail, the dispersion effects of periodic Mo/Si multilayer mirrors with N = 2, 8, 14 on incident attosecond pulses with τ0 = 100 as were analyzed both in temporal and spectral domains. The reflected pulse temporal intensities and the spectral group delay dispersion of the multilayer mirrors are shown in Fig. 3.

Table 1.

The PBFd and ELFd of periodic Mo/Si multilayer mirrors with Nmax in the condition of incident attosecond pulses with τ0 = 100 as, 200 as, 300 as, 400 as, and 500 as.

.
Fig. 3. (a) The reflected pulse temporal intensities and (b) the spectral group delay dispersion of the multilayer mirrors with N = 2, 8, 14 respectively for the incident pulse with τ0 = 100 as when only the dispersion effect of the multilayer mirror was considered.

In Fig. 3(a), the peak intensity of the reflected pulse decreases from 0.9862 to 0.5596 when N increases from 2 to 8 (i.e., Nmax for τ0 = 100 as), then increases to 0.5748 when N increases to 14, while the duration of the reflected pulse increases from 101.39 (near-transform-limited) as to 178.67 as, then decreases to 173.96 as. In Fig. 3(b), except the periodic Mo/Si multilayer mirror with N = 2, the ones with N = 8, 14 both exhibit sharp group delay dispersion ripples in the spectral region of the incident pulse. These ripples are deleterious for incident pulses because they can cause pre- and post-pulses in time domain (as shown in Fig. 3(a)) and can seriously decrease the fraction of the energy in the main pulse, thus increase the pulse duration. Consequently, the multilayer with N = 8 (Nmax) causes the most serious energy loss and pulse broadening because it shows the largest group delay dispersion ripple in the spectral region of the incident pulse, which coincides with the results shown in Fig. 2.

Meanwhile, in Fig. 2, both PBFd and ELFd decrease with the increase of τ0, which indicates the incident pulse with a smaller duration suffers from more serious energy loss and pulse broadening. To determine the reason, we analyzed the effects of dispersion of the periodic Mo/Si multilayer mirror with N = 20 on incident attosecond pulses with τ0 = 100 as, 300 as, 500 as. The reflected pulse temporal intensities of three cases are shown in Fig. 4(a). When τ0 increases from 100 as to 500 as, the peak intensity of the reflected pulse increases from 0.5914 to 0.9459, while the pulse broadening factor PBF decreases from 1.6908 to 1.0572 (near-transform-limited). More serious energy loss and pulse broadening for the incident pulse with smaller τ0 should be blamed on the larger and more group delay dispersion ripples exhibited in the spectral region of the incident pulse, as shown in Fig. 4(b).

Fig. 4. (a) The reflected pulse temporal intensities and (b) the spectral group delay dispersion of the multilayer mirror with N = 20 for incident pulses with τ0 = 100 as, 300 as, 500 as when only the dispersion effect of the multilayer mirror was considered.
3.2. The effect of filtering on attosecond pulses

Besides the dispersion effect, the spectrum filtering of a periodic Mo/Si multilayer mirror is another main effect on an incident attosecond pulse. Hence, we studied the filtering effect of periodic Mo/Si multilayer mirrors with different bi-layers (N = 1–50) on incident attosecond pulses with various durations (τ0 = 100 as, 200 as, 300 as, 400 as, 500 as) by calculating the pulse broadening factor PBFf and the energy loss factor ELFf (Fig. 5).

Fig. 5. (a) The pulse broadening factor PBFf and (b) the energy loss factor ELFf describing the filtering effect of periodic Mo/Si multilayer mirrors with N = 1–50 on incident attosecond pulses with τ0 = 100 as, 200 as, 300 as, 400 as, 500 as.

For each incident pulse, PBFf increases rapidly at first, then slight decreases before remaining constant, while ELFf decreases rapidly at first, then remains constant. To understand the varied trends of PBFf and ELFf with changing N shown in Fig. 5, the filtering effects of periodic Mo/Si multilayer mirrors with N = 5, 10, 15, 20, 25 on incident attosecond pulses with τ0 = 100 as were analyzed particularly. The reflected pulse temporal intensities are shown in Fig. 6(a). For periodic Mo/Si multilayer mirrors with different N, the temporal shapes of the reflected pulses are similar, but their peak intensities and durations are different, as shown in Table 2. When N increases from 5 to 15, the duration of the reflected pulse τ1 increases from 171 as to 229 as, while the peak intensity increases from 0.0582 to 0.0696. Then, when N keeps rising from 15 to 25, τ1 still increases from 229 as to 234 as, but decreases from 0.0696% to 0.0582%. To explain the results, we studied the reflective performances of five multilayer mirrors in the frequency domain (Fig. 6(b)), and calculating their reflective bandwidth ΔE and the peak reflectivity Rpeak, as shown in Table 2.

Fig. 6. (a) The reflected pulse temporal intensities and (b) the group delay dispersion of the periodic Mo/Si multilayer mirrors with N = 5, 10, 15, 20, 25 for the incident pulse with τ0 = 100 as when only the filtering effect of the multilayer mirror was considered.
Table 2.

Temporal and spectral parameters of periodic Mo/Si multilayers with N = 5, 10, 15, 20, 25 for incident pulse with τ0 = 100 as.

.

In Table 2, with the increase of N, the bandwidth ΔE of the periodic Mo/Si multilayer mirrors decreases from 12.79 eV to 5.09 eV. The result indicates that the periodic Mo/Si multilayer with larger N exhibits a more serious filtering effect for an incident pulse, which leads to larger pulse broadening according to the Fourier theory.[26] On the other hand, the irregular varying of the peak intensity with the increase of N is the interactive result of the decrease of ΔE and the increase of Rpeak, because the decrease of ΔE causes pulse broadening, thus decreases , while the increase of Rpeak promotes . Hence, there is a tradeoff between ΔE and Rpeak for changing , which leads to the irregular varying of with the increase of N.

In Fig. 5, we can see that PBFf and ELFf both decrease with the increase of τ0, which means that the incident pulse with a smaller duration suffers from more serious energy loss and pulse broadening. To determine the reason, we analyzed the filtering effect of the periodic Mo/Si multilayer mirror with N = 20 on incident attosecond pulses with τ0 = 100 as, 300 as, 500 as particularly. The temporal intensities of three cases are shown in Fig. 7(a). When τ0 increases from 100 as to 500 as, the peak intensity of the reflected pulse increases from 0.069 to 0.3716, while the pulse broadening factor PBF decreases from 2.33 to 1.26. The incident pulse with smaller τ0 undergoes more serious energy loss and pulse broadening, because the multilayer mirror filters more spectral components of the incident pulse, as shown in Fig. 7(b).

Fig. 7. (a) The reflected pulse temporal intensities and (b) the spectral group delay dispersion of the multilayer mirror with N = 20 for incident pulses with τ0 = 100 as, 300 as, 500 as when only the filtering effect of the multilayer mirror was considered.
3.3. Comparison of the effects of dispersion and filtering

In this section, we compared the dispersion and filtering effects induced by periodic Mo/Si multilayer mirrors reflection by calculating the ratios of pulse broadening factor PBF and the energy loss factor ELF (i.e., PBFd/PBFf and ELFd/ELFf), as shown in Fig. 8.

Fig. 8. (a) The ratio of the pulse broadening factor PBF (PBFd/PBFf) and (b) the energy loss factor ELF (ELFd/ELFf) of two effects in the condition of periodic Mo/Si multilayer mirrors with N = 1–50 for incident attosecond pulses with τ0 = 100–500 as.

The small PBFd/PBFf (blue region in Fig. 8(a)) always shows in the region of large N and small τ0, while the large PBFd/PBFf (red region in Fig. 8(a)) exhibits in the region of small N and large τ0. The results indicate that with the increase of N or the decrease of τ0, the pulse broadening induced by the filtering effect of the multilayer mirror will become more and more serious than the one induced by the dispersion effect. In addition, with the varying of N and τ0, the values of PBFd/PBFf are almost smaller than 1, indicating that the filtering effect of periodic Mo/Si multilayer mirrors should take more responsibility for pulse broadening than the dispersion effect. The irregular changing of PBFd/PBFf in the region of small τ0 and N shown in Fig. 8(a) is attributed to the sharp varying of PBFd with the increase of N, as shown in Fig. 2(a).

In contrast with the pulse broadening case, the small ELFd/ELFf (blue region in Fig. 8(b)) always shows in the region of small N and large τ0, which indicates that with the decrease of N or the increase of τ0, the energy loss induced by the filtering effect of the multilayer mirror will become more and more obvious than the one induced by the dispersion. Compared with the results shown in Figs. 8(a) and 8(b), we conclude that the filtering effect of a periodic Mo/Si multilayer mirror is the dominant reason for the pulse broadening and energy loss of an incident attosecond pulse.

4. Conclusions

In this paper, we studied the effects of dispersion and filtering induced by Mo/Si multilayer mirrors reflection on attosecond pulses. The pulse broadening factor and the energy loss factor were calculated for incident attosecond pulses with various durations. When only the dispersion effect of the periodic multilayer mirror was considered, the pulse broadening factor and the energy loss factor both increase rapidly at first, then decrease slowly with the increase of the bi-layer number of a periodic multilayer. In addition, both the pulse broadening factor and the energy loss factor decrease with the increase of the duration of an incident pulse. By investigating the temporal and spectral performances of the periodic multilayer mirrors, we concluded that the more and larger group delay dispersion ripple of the multilayer in the spectral region of the incident pulse can cause more serious energy loss and pulse broadening. When only the filtering effect of the multilayer mirror was considered, the periodic Mo/Si multilayer with more bi-layers exhibits a more serious filtering effect for an incident pulse, which leads to larger pulse broadening according to the Fourier theory. In addition, there is a tradeoff between reflective bandwidth and peak reflectivity for pulse energy loss, which leads to the irregular varying of energy loss with the increase of multilayer bi-layers. Furthermore, the pulse broadening factor and the energy loss factor both decrease with the increase of multilayer bi-layers, which indicates that the incident pulse with a smaller duration suffers from more serious energy loss and pulse broadening. Finally, by comparing the dispersion and filtering effects of periodic Mo/Si multilayer mirrors on incident attosecond pulses, we conclude that the filtering effect of a periodic Mo/Si multilayer mirror is the dominant reason for the pulse broadening and energy loss for an incident attosecond pulse which is reflected by this mirror. The research on the effects of dispersion and filtering induced by periodic Mo/Si multilayer mirror reflection on attosecond pulses can improve the understanding of the origins of pulse broadening and pulse energy loss induced by periodic multilayer mirrors reflection, and give a guide for attosecond multilayer mirrors design.

Reference
1Hentschel MKienberger RSpielmann ChReider G AMilosevic NBrabec TCorkum PHeinzmann UDrescher MKrausz F 2001 Nature 414 509
2Zhan M JYe PTeng HHe X KZhang WZhong S YWang L FYun C XWei Z Y 2013 Chin. Phys. Lett. 30 093201
3Zhao KZhang QChini MWu YWang X WChang Z H 2012 Opt. Lett. 37 3891
4Chini MZhao KChang Z 2014 Nat. Photonics 8 178
5Medisauskas LWragg Jvan der Hart HIvanov M Y 2015 Phys. Rev. Lett. 115 153001
6He L XLan P FZhang Q BZhai C YWang FShi W JLu P X 2015 Phys. Rev. 92 043403
7Luo X YBen SGe X LWang QFuo JLiu X S 2015 Acta Phys. Sin. 64 193201 (in Chinese)
8Wu JZhai ZLiu X S 2010 Chin. Phys. 19 093201
9Drescher MHentschel MKienberger RTempea GSpielmann CReider G ACorkum P BKrausz F 2001 Science 291 1923
10Kienberger RHentschel MUiberacker MSpielmann ChKitzler MScrinzi AWieland MWesterwalbesloh ThKleineberg UHeinzmann UKrausz F 2002 Science 297 1144
11Abel M JPfeifer TNagel P MBoutu WBell M JSteiner C PNeumark D MLeone S R 2009 Chem. Phys. 366 9
12Zhan M JYe PTeng HHe X KZhang WZhong S YWang L FYun C XWei Z Y 2013 Chin. Phys. Lett. 30 093201
13Lin C YChen S JLiu D HLiu Y W 2012 IEEE Photonics 4 1281
14Beigman I LPirozhkov A SRagozin E N 2001 JETP Lett. 74 149
15Beigman I LPirozhkov A SRagozin E N 2002 J. Opt. A: Pure Appl. Opt. 4 433
16Lin C YLiu D H 2012 Chin. Phys. 21 094216
17Lin C YChen S JLiu D H 2013 Chin. Phys. 22 014210
18Lin C YChen S JLiu D H 2013 Optik 124 990
19Meekins J FCruddace R GGursky H 1987 Appl. Opt. 26 990
20Henke B LGullikson E MDavis J C 1993 At. Data Nucl. Data Tables 54 181
21Aquila A LSalmassi FDollar FLiu YGullikson E M 2006 Opt. Express 14 10073
22Ksenzov DGrigorian SPietsch U 2008 J. Synchrotron Radiat. 15 19
23Ksenzov DGrigorian SHendel SBienert FSacher M DHeinzmann UPietsch U 2009 Phys. Status Solidi 206 1875
24Wonisch ANeuhäusler UKabachnik N MUphues TUiberacker MYakovlev VKrausz FDrescher MKleineberg UHeinzmann U 2006 Appl. Opt. 45 4147
25Suman MFrassetto FNicolosi PPelizzo M G 2007 Appl. Opt. 46 8159
26Aquila ASalmassi FGullikson E 2008 Opt. Lett. 33 455