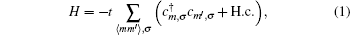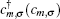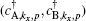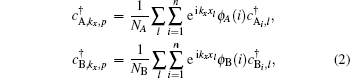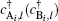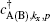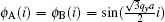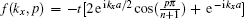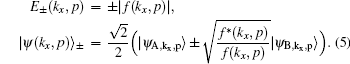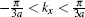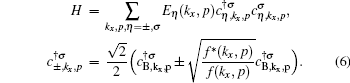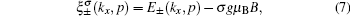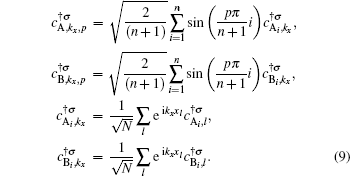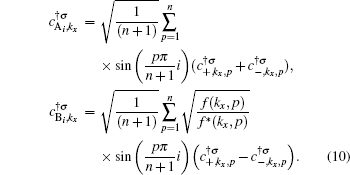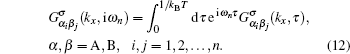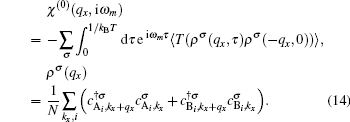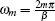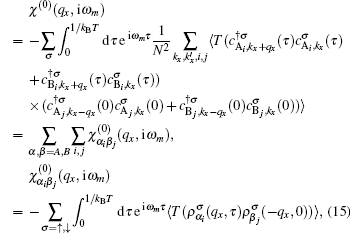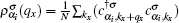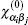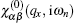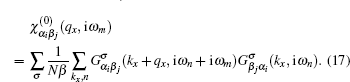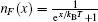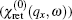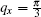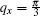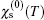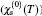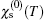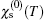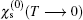Cite this Article
Rezania H, Azizi F. Charge susceptibilities of armchair graphene nanoribbon in the presence of magnetic field. Chinese Physics B, 2016, 25(9): 097303  
Permissions
Charge susceptibilities of armchair graphene nanoribbon in the presence of magnetic field
Rezania H†, , Azizi F
Department of Physics, Razi University, Kermanshah, Iran

 

† Corresponding author. E-mail: rezania.hamed@gmail.com

Abstract
Abstract

We present the behaviors of both dynamical and static charge susceptibilities of undoped armchair graphene nanoribbon using the Green’s function approach in the context of tight binding model Hamiltonian. Specifically, the effects of magnetic field on the the plasmon modes of armchair graphene nanoribbon are investigated via calculating the correlation function of charge density operators. Our results show that the increase of magnetic field makes the high-frequency plasmon mode for both metallic and insulating cases disappear. We also show that low-frequency plasmon mode for metallic nanoribbon appears due to increase of magnetic field. Furthermore, the number of collective excitation modes increases with ribbon width at zero magnetic field. Finally, the temperature dependence of the static charge structure factor of armchair graphene nanoribbon is studied. The effects of both magnetic field and ribbon width on the static charge structure factor are discussed in detail.

PACS: 73.22.–f;72.80.Vp;73.63.–b
Keyword:armchair graphene nanoribbon;Green’s function
1. Introduction

Graphene is a newly realized two-dimensional electron system that has attracted a great deal of interest because of the new physics it exhibits and its potential as new material for electronic technology.[1–4] Graphene consists of a single atomic layer of graphite, which can also be viewed as a sheet of unrolled carbon nanotube. Several anomalous phenomena ranging from half integer quantum Hall effect, nonzero Berry’s phase,[5] to minimum conductivity[2] have been observed in experiments. The carriers in graphene behave as massless relativistic Dirac fermions with an effective speed of light c = 106 m/s within the low-energy range (ε < 0.5 eV).[5] The chirality and a Berry phase of π at the two Dirac points provide an environment for highly unconventional and fascinating two-dimensional electronic properties, such as the absence of backward scattering,[6,7] Klein tunneling[4] and the π phase shift of the Shubinkov–de Haas oscillations.[8] Ribbons with a finite width of graphene, referred to as graphene nanoribbons, have also been studied extensively.[9–11] Recent experiments show that it is possible to make graphene nanoribbons with various widths by using the mechanical method [12] and the epitaxial growth[12] method. The successive miniaturization of graphene-based electronic devices requires clarification of the effect of edges on the electronic structure and electronic transport properties of nanometer-sized graphene. The presence of edges in graphene has strong implications for the low-energy spectrum of the π-electrons.[9,10] There are two basic edge shapes, armchair and zigzag, which determine the properties of graphene ribbons. It was shown that ribbons with zigzag edges possess localized edge states with energies close to the Fermi level.[10,13] In contrast, edge states are absent for ribbons with armchair edges. Because zigzag edges can induce a strong magnetic response,[13–15] considerable effort has been devoted to studying the effect of edges in graphitic nanomaterials.

The analytical wave function and energy dispersion of zigzag nanoribbon have been derived by several research groups.[16,17] For armchair graphene nanoribbons, the analytical forms of wave functions within the low-energy range have been worked out based on the effective mass approximation.[18] It is predicted that all zigzag graphene nanoribbons are metallic with localized states on the edges[16,17] while armchair graphene nanoribbons are either metallic or insulating, depending on their widths.[16,18] Based on a theoretical paper, a general analytical expression of wave function and eigenenergy in armchair graphene nanoribbons has been derived.[19] Due to the quantum confinement, the spectrum breaks into a set of subbands and the wave vector along the confined direction becomes discretized, which is similar to the case of carbon nanotubes.[20]

In order to study electronic properties of electron gas in the nano structures and graphene, the dynamical polarizability whereby the screening effects have been found is required.[21,22] The static structure factor at Fermi wave vector that gives the Thomas–Fermi screening length is important for transport properties of two-dimensional graphene.[23,24] The dynamical polarizability renormalizing the phononic Green’s function can explain the phonon softening and Kohn anomaly phenomenon[25] at the Γ point. The charge response function was studied for gapped graphene[26] and graphene in the presence of magnetic field.[27] A semi-analytical expression for the dynamical density–density linear response function of doped graphene sheet within Dirac approximation at finite temperature has been performed.[28] Their results demonstrated that the fluctuations of density in bilayer case can present either single-component massive-chiral character or standard two-layer character, depending on energy and doping. The spin transport of fermions is central to many fields of physics. Electron transport runs modern technology and electron spin is being explored as a new carrier of information.[29] The paramagnetic spin susceptibility shows behavior similar to the charge compressibility which decreases as the interaction increases at zero temperature. Sheehy and Schmalian studied orbital diamagnetic susceptibility of undoped graphene by using a renormalization group approach.[30] Their studies show that the temperature dependence of diamagnetic susceptibility of undoped graphene is quite different from the two-dimensional electron gas and it behaves like T/|ln(T)|2.

In the calculation of high-energy corrections to the charge and spin response, both inter and intraband transitions contribute to the frequency behavior of dynamical polarizability. Recently, a theoretical work provided a study of both imaginary and real parts of non-interacting polarizability of graphene within an analytical approach.[31] The authors found there is no noticeable angle dependence for the imaginary part of polarizability around the van Hove singularity, i.e., ħω/t = 2.0, where t implies the nearest neighbor hopping integral. Also it has been shown that the Dirac approximation has a good agreement with the analytical expression for the imaginary part of the charge response in the low-frequency region.[31] In a theoretical work, the paramagnetic susceptibility of zigzag graphene nanoribbons has been calculated.[32] Because the edge states lead to a sharp peak in the density of states at the Fermi level, the graphite ribbons with zigzag edges show Curie-like temperature dependence of the Pauli paramagnetic susceptibility.[32]

The goal of this work is to study the effects of magnetic field and ribbon width on plasmon frequencies of undoped armchair graphene nanoribbons at finite temperature. In order to obtain these collective modes, we study the magnetic field and ribbon width dependence of dynamical charge susceptibility as a function of frequency in the context of tight binding model Hamiltonian. The frequency positions of sharp peaks in dynamical charge susceptibility introduce the plasmonic oscillations of the mentioned nanostructure. Furthermore the temperature dependence of static charge susceptibility of armchair nanoribbon affected by variation of magnetic field has been studied. The effects of ribbon width on the behavior of static and dynamical charge susceptibilities have been focused. Green’s function approach has been implemented to calculate the charge susceptibility, i.e., the time-ordered charge density correlation function. In the last section, we discuss and analyze our results to show how external magnetic field and ribbon width affect the frequency of collective modes.

2. Theoretical formalism

The lattice structure of armchair graphene nanoribbons consists of two types of sublattices A and B as shown in Fig. 1. The unit cell contains n A-type atoms and n B-type atoms. Based on the translational invariance, we choose the plane wave basis along the x direction. In this section, we employ a single-orbital nearest neighbor tight-binding model in order to study the electronic states of nanographite ribbons. This model has been successfully used for the calculation of electronic states of fullerene molecules, carbon nanotubes, and other carbon-related materials. In the absence of the magnetic field, the Hamiltonian is written as

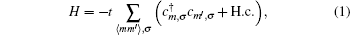
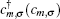
where ⟨ mm′⟩ denotes the nearest neighbors; H.c. stands for the Hermitian conjugate; operators create (annihilate) an electron at mth site of the lattice with spin σ. Also t is the nearest neighbor hopping integrals. Each index site m can be expressed as l, Ai or l, Bi, where l denotes the unit cell index and Ai(Bi) implies carbon atom located at A (B) sublattice. Moreover, i implies the position of A or B atoms along the y direction according to Fig. 1, so that the maximum value of i is the width of the ribbon, i.e., n. 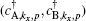In order to obtain the electronic band structure of the system, we consider the following expansions for the wave functions of A and B sublattices in operator form :[19]

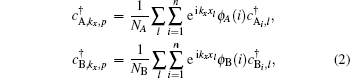
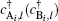
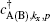
where creates an electron in the pz orbit of a carbon atom located at A (B) sublattices with position i along the width of ribbon, i.e., y direction (see Fig. 1) on the l-th unit cell. The xl denotes the position of l-th unit cell along the x direction, as shown in Fig. 1. Also creates an electron at A(B) sublattices with wave vector kx and quantum number p which is introduced in the following. Employing the hard-wall boundary condition,[19] one can choose . 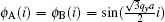Then the hard-wall boundary condition implies

Here, qy is the discretized wave vector in the y direction, a = 1.42 Å is the bond length between carbon atoms, and n introduces the width of ribbon. Applying the normalization condition, the normalized coefficients, NA and NB, have been obtained as [19] so that N is the number of unit cells along the x direction. After writing the matrix form of tight binding model Hamiltonian in terms of basis kets {|ψA,kx,p⟩,|ψB,kx,p⟩}, we get the following expression:

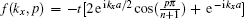
where . Solving Eq. (4) in its matrix form, we obtain the band energy dispersions and band wave functions as

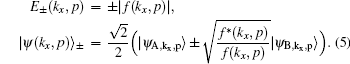
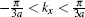
Here, ± denotes the conduction and valence bands, respectively. Also the wave vector kx belongs to the first Brillouin zone of atomic chain with lattice constant 3a (see Fig. 1). Thus, is required. Based on band wave functions in Eq. (5), the Hamiltonian in Eq. (4) can be rewritten as

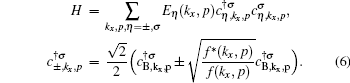
It should be noted that the in-plane magnetic field couples not only to the spin degrees of freedom in a quasi-two-dimensional electron gas such as graphene nanoribbon which leads to the spin polarization of the carriers,[33–35] due to finite quantum well thickness. However, because of the absence of thickness in graphene, the applied magnetic field couples only with spin of the carriers and leads to their spin polarization. Therefore, we add the Zeeman energy term to the original model Hamiltonian and consequently each electronic level splits into two separate sublevels for spin up and down electrons. Such effect can be readily considered via redefinition of electronic energy bands as follows:

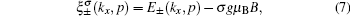
where μB is the Bohr magneton, g refers to gyromagnetic constant, and B denotes the external magnetic field strength. Due to redefined energy bands in Eq. (7), we find the Hamiltonian form in the presence of magnetic field as

Using expression for qy in Eq. (3), one can rewrite Eq. (2) as follows:

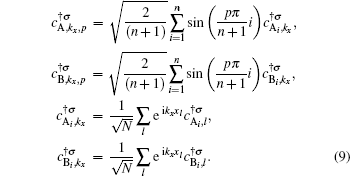
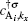
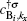
Using Eqs. (6) and (12), we can readily express operators and in terms of band operators

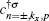
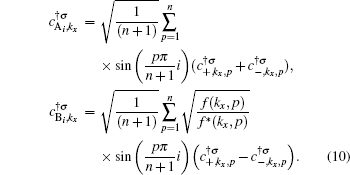
Since each unit cell of armchair graphene nanoribbon includes 2n atoms with types A and B, Green’s function can be written as the 2n × 2n matrix. In the Matsubara formalism,[21] the matrix elements of Green’s function are defined by

where τ is imaginary time. The Fourier transformation of each above matrix element of Green’s function is calculated by

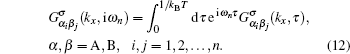
Here, ωn = (2n + 1)πkBT denotes the fermionic Matsubara frequency in which T is equilibrium temperature. Based on the operator transformation in Eq. (10), the Fourier transformations of Green’s function matrix elements are finally given by

The quantity of interest for studying many particle properties such as plasmon oscillations and phonon softening is the dynamical charge response function. Also this quantity determines the effective electron–electron interaction and the Friedel oscillations. Linear response theory gives us the noninteracting charge response function (χ(0)) based on the correlation function of density–density operators (ρ) as

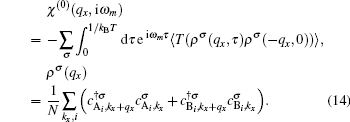
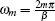
Here, N is the number of unit cells in the lattice, and denotes the Bosonic Matsubara frequency. After substitution of operator form of electronic density into the correlation function, we arrive at the following expression for χ(0):

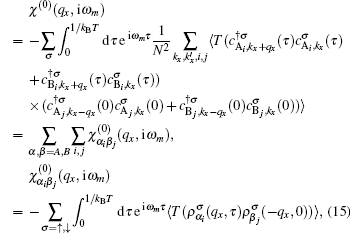
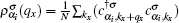
so that we have . Since applying magnetic field leads to long-range magnetic ordering for graphene nanoribbon, the contribution of electrons with spin down to the response function is different from that of electrons with spin up. In order to calculate the correlation function in Eq. (15), one particle spin-dependent Green’s function in Eq. (13) should be exploited. Wick’s theorem has been applied to express the charge response in terms of matrix elements of non-interacting electronic Green’s function. 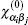Each element of charge response function matrix, i.e., , can be expressed in terms of Green’s function elements as

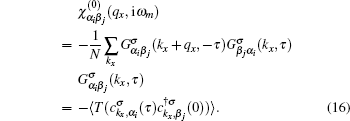
In order to find the collective spectrum of the quantum system, the Fourier transformation to the energy space is required. Using the Fourier transformation in Matsubara’s representation,[21] 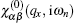in Eq. (15) can be written as

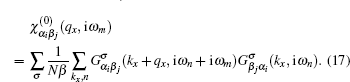
Substituting Green’s function matrix elements introduced in Eq. (13) into Eq. (17) and performing Matsubara frequency summation over fermionic Matsubara energies ωn lead to the following expression for dynamical charge susceptibility of electrons on the armchair graphene nanoribbon lattice according to Eq. (15):

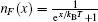
where is the Fermi–Dirac distribution function. The effects of magnetic field on the charge response function comes from factor ξ which has been defined in Eq. (7) Note that the frequencies of collective charge modes are determined by the position of peaks in the imaginary part of the delayed form of dynamical charge susceptibility. The delayed form of charge and susceptibility are found by performing the analytic continuation iωm → ω + i0+. Static charge susceptibility can be readily obtained using limitation χ(0)(qx,ω → 0). In the next section, we present the numerical results of both dynamical and static charge susceptibilities of armchair graphene nanoribbon.

3. Numerical results and discussion

In this section, we present our main numerical results for dynamical and static charge susceptibilities of undoped armchair graphene nanoribbon in the presence of magnetic field. This susceptibility is associated with the imaginary part of dynamical correlation function between charge operators introduced in Eq. (18). In the following, the frequency behavior of dynamical susceptibilities is studied at fixed wave number 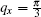. The temperature behavior of static charge response function is also studied at 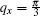. The half filling constraint has been considered for armchair graphene nanoribbon. In other words, the electronic chemical potential is set to zero.

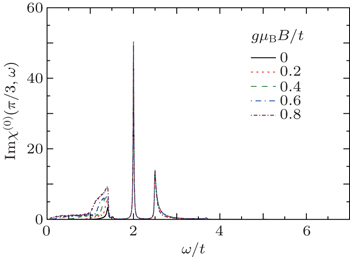
Fig. 1. Structure of an armchair graphene nanoribbon, consisting of sublattices, A and B. n is the width of the ribbon. Every unit cell contains n A and B sublattices. Two additional hard walls (j = 0,n + 1) are imposed on both edges.

The imaginary part of noninteracting polarizability (Imχ(0)(π/3,ω)) of armchair carbon nanoribbon with width n = 4 for different values of magnetic field at fixed temperature kT/t = 0.05 has been plotted versus normalized frequency in Fig. 2. Sharp peak in the imaginary part of charge susceptibility is related to collective excitation mode or plasmon frequency. Each curve in Fig. 2, corresponding to a fixed value of magnetic field, presents a sharp peak at normalized frequency ω/t ≈ 1.4. The height of this plasmon peak is clearly independent of magnetic field according to Fig. 2. Another plasmon peak appears at normalized frequency ω/t ≈ 2.4 for all values of magnetic fields gμB/t. Furthermore, the intensity of plasmon mode reduces with magnetic field at this frequency. Also we observe a low-frequency sharp plasmon peak with high intensity for charge susceptibility of armchair nanoribbon n = 4 for magnetic fields gμB/t = 0.6,0.8. The other values of magnetic fields do not present such plasmon oscillation. Dynamical charge susceptibility vanishes at high frequencies larger than 3.0 for all values of magnetic field. In Fig. 3, we have plotted the imaginary part of dynamical charge susceptibility of metallic armchair carbon nanoribbon with width n = 5 versus normalized frequency ω/t for different magnetic fields, namely, gμB/t = 0.0,0.2,0.4,0.6,0.8 for fixed temperature kBT/t = 0.05. A plasmon mode with high intensity is clearly observed at ω/t = 2.0 for all normalized magnetic fields. At ω/t ≈ 1.4, a low-intensity plasmon mode appears for all values of magnetic field; however its intensity raises with magnetic field. The peak in higher magnetic fields becomes sharper compared to lower ones. Furthermore, a low-intensity plasmon peak is observable at ω/t ≈ 2.5 for all magnetic fields. In addition, the imaginary part of dynamical charge susceptibility vanishes for magnetic fields above 3.0 as shown in Fig. 3.

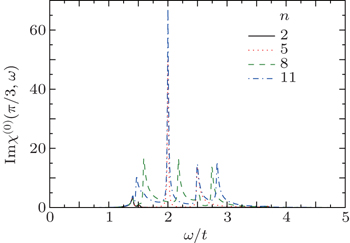
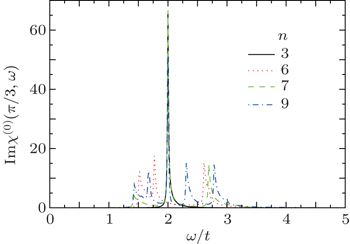
Fig. 2. Imaginary part of dynamical charge susceptibility (Imχ(0)(π/3,ω)) of insulating armchair graphene nanoribbon with width n = 4 as a function of normalized frequency ω/t for different values of magnetic field for fixed temperature kBT/t = 0.05.
Fig. 3. Imaginary part of dynamical charge susceptibility (Imχ(0)(π/3,ω)) of metallic armchair graphene nanoribbon with width n = 5 as a function of normalized frequency ω/t for different values of magnetic field for fixed temperature kBT/t = 0.05.

We have also studied the effect of ribbon width on plasmon peaks of both metallic and insulating armchair nanoribbons. Figure 4 presents the frequency behavior of imaginary part of dynamical charge susceptibility of metallic armchair nanoribbon for different widths and zero magnetic field. Collective modes take place in frequency region 1.25 < ω/t < 3.25 for all ribbon widths. A considerable plasmon with high intensity occurs at ω/t = 2.0 for widths n = 5 and n = 11. Low-intensity plasmon modes for n = 11 appears at frequencies ω/t = 1.5,2.5,2.85. The number of plasmon modes of armchair nanoribbon with n = 11 is larger than the other widths. Figure 4 implies that the case of ribbon with width n = 2 shows no collective modes on the whole range of frequency region. In Fig. 5, we depict Imχ(0)(π/3,ω) of insulating armchair nanoribbon as a function of frequency for different widths, namely, n = 3,6,7,9 at kBT/t = 0.05 in the absence of magnetic field. Similar to metallic nanoribbon cases, plasmon modes appear in frequency region 1.25 < ω/t < 3.25 for all ribbon widths. According to Fig. 5, a plasmon frequency with high intensity takes place at ω/t = 2.0 for widths n = 3,7,9. Furthermore, the number of plasmon modes increases with ribbon width, so that metallic ribbon n = 9 has five plasmon modes in its excitation spectrum.

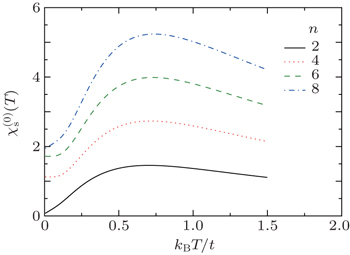
Fig. 4. Imaginary part of dynamical charge susceptibility (Imχ(0)(π/3,ω)) of metallic armchair graphene nanoribbons as a function of normalized frequency ω/t for different widths and for zero magnetic field, kBT/t = 0.05.
Fig. 5. Imaginary part of dynamical charge susceptibility (Imχ(0)(π/3,ω)) of insulating armchair graphene nanoribbons as a function of normalized frequency ω/t for different widths and for zero magnetic field, kBT/t = 0.05.

The characteristic results for static charge structure factor (χ(0)(T)) of armchair carbon nanoribbons with different widths, namely n = 2,4,6,8 at wave number qx = π/3 are presented in Fig. 6. There is a peak in the structure factor which moves to higher temperature upon increasing ribbon width n. Our data show that the height of the peak in the static structure factor increases with n. A novel feature pronounced in Fig. 6 is nonzero value for static structure factor of insulating graphene nanoribbons when temperature tends to be zero. This result is in contrast to the Fermi liquid theory which states that the static structure factor at low temperatures is proportional to density of states at the Fermi level energy. Therefore, the Fermi liquid theory loses its validity for quasi-one-dimensional nanoribbon systems. In addition, the static charge structure factor is evidence for charge ordering of electronic system. Each curve in Fig. 6 indicates 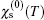increases with temperature until it reaches a maximum and then it exponentially goes to zero. This behavior implies that temperature causes charge ordering up to a maximum point and then the increase in temperature leads to decreasing charge ordering.

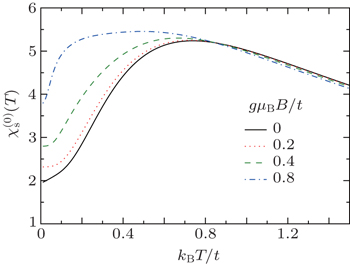
Fig. 6. Static charge susceptibility of armchair graphene nanoribbons as a function of normalized temperature kBT/t for different widths and for zero magnetic field.

Finally, we turn our attention to the effect of magnetic field on the static charge structure factor of graphene nanoribbon. In Fig. 7, we have plotted the temperature behavior of 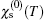of undoped armchair nanoribbon n = 8 for different magnetic fields. A broad peak in 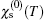has been clearly observed for normalized magnetic fields gμBB/t = 0,0.2,0.4,0.8. For kBT/t < 1.0, static structure factor increases with magnetic field at fixed values of normalized temperatures. Moreover, a nonzero value for 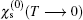is obtained for each magnetic field. For kBT/t > 1.0, the static charge structure factor is clearly independent of gμBB/t, where all plots fall on each other.

Fig. 7. Static charge susceptibility of metallic armchair graphene nanoribbons with width n = 8 as a function of normalized temperature kBT/t for different magnetic fields.
4. Summary

In conclusion, we have presented the charge susceptibilities of armchair graphene nanoribbons in the presence of in-plane magnetic field. In the context of tight binding model Hamiltonian and by using Green’s function approach, the electronic excitation spectrum has been studied. Using linear response theory, the charge response function of nanoribbon graphene has been obtained. Specifically, the effects of ribbon width and magnetic field on the temperature dependence of static charge susceptibility have been investigated. Also the results show that there is resonance plasmon peak in dynamical charge susceptibility for all magnetic fields and ribbon width.

Reference
1Geim K AMacDonald A H2009Phys. Today6035
2Novoselov K SGeim A KMorozov S VJiang DZhang YDubons S VGrigorieva I VFirsov A A 2004 Science 306 666
3Ohta TBostwick BSeyller THorn KRorenberg E 2006 Science 313 951
4Katsnelson M INovoselov K SGeim A K 2006 Nat. Phys. 2 620
5Zhang YTan T WStormer H LKim P 2005 Nature 438 201
6Ando TNakanishi T 1998 J. Phys. Soc. Jpn. 67 1704
7Ando TNakanishi TSaito R 1998 J. Phys. Soc. Jpn. 67 2857
8Luk’yanchuk I AKopelevich Y 2004 Phys. Rev. Lett. 93 166402
9Fujita MWakabayashi KNakada KKusakabe K 1996 J. Phys. Soc. Jpn. 65 1920
10Nakada KFujita MDresselhaus GDresselhaus M S 1996 Phys. Rev. 54 17954
11Ezawa M 2006 Phys. Rev. 73 045432
12Berger C 2004 J. Phys. Chem. 108 19912
13Wakabayashi KSigrist MFujita M 1998 J. Phys. Soc. Jpn. 67 2089
14Son Y WCohen M LLouie S G 2006 Nature 444 347
15Son Y WCohen M LLouie S G 2006 Phys. Rev. Lett. 97 216803
16Sasaki KMurakami SSaito R 2006 J. Phys. Soc. Jpn. 75 074713
17Sasaki KMurakami SSaito R 2006 Appl. Phys. Lett. 88 113110
18Brey LFertig H A 2006 Phys. Rev. 73 235411
19Zheng HWang Z FLuo TShi Q WChen J 2007 Phys. Rev. 75 165414
20Ajiki HAndo T 1993 J. Phys. Soc. Jpn. 62 1255
21Mahan G D1993Many Particle PhysicsNew YorkPlenumn Press
22Grosso GParravincini G P2003Solid State PhysicsNew YorkAcademic Press
23Ando T 2006 J. Phys. Soc. Jpn. 75 074716
24Stauber TPeres N MGuinea F 2007 Phys. Rev. 76 205423
25Castro Neto A HGuinea F 2007 Phys. Rev. 75 045404
26Pyatkovskiy P K 2009 J. Phys.: Condens. Matter 21 025506
27Roldan RFuchs J NGeorbig M O 2009 Phys. Rev. 80 085408
28Ramezanali M RVazifeh M MAsgari RPolini MMacdonald A H 2009 J. Phys. A: Math. Theor. 42 214015
29Wolf S A 2001 Science 294 1488
30Sheehy D ESchmalian J 2007 Phys. Rev. Lett. 99 226803
31Stauber TSchliemann JPeres N M 2010 Phys. Rev. 81 085409
32Wakabayashi KFujita MAjiki HSigrist M 1999 Phys. Rev. 59 8271
33Zhang YDas Sarma S 2006 Phys. Rev. Lett. 96 196602
34Subasi A LTanatar B 2008 Phys. Rev. 78 155304
35Palo S DBotti MMoroni SSenatore G 2005 Phys. Rev. Lett. 94 226405